Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T04:59:47.444Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-well-foundedness of well-orderable power sets

Published online by Cambridge University Press:  12 March 2014

T. E. Forster  and
J. K. Truss
T. E. Forster
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge, CB3 0WB, UK, E-mail: [email protected]
J. K. Truss
Affiliation:
Department of Pure Mathematics, University of Leeds, Leeds LS2 9JT, UK, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Tarski [5] showed that for any set X, its set ω(X) of well-orderable subsets has cardinality strictly greater than that of X, even in the absence of the axiom of choice. We construct a Fraenkel-Mostowski model in which there is an infinite strictly descending sequence under the relation ∣ω(X)∣ = ∣Y∣. This contrasts with the corresponding situation for power sets, where use of Hartogs' ℵ-function easily establishes that there can be no infinite descending sequence under the relation .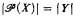

Keywords

well-orderablewell-foundedcardinal number
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 68 , Issue 3 , September 2003 , pp. 879 - 884
Copyright
Copyright © Association for Symbolic Logic 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Forster, T. and Kaye, R., End-extensions preserving power set, this Journal, vol. 56 (1991), pp. 323–328.Google Scholar
[2] Jech, T. and Sochor, A., Applications of the θ-model, Bulletin de l'Académie Polonaise des Sciences, vol. 14 (1966), pp. 297–303 and 351–355.Google Scholar
[3] Kirmayer, G., A refinement of Cantor's theorem, Proceedings of the American Mathematical Society, vol. 83 (1981), p. 774.Google Scholar
[4] Mathias, A. R. D., The strength of Mac Lane set theory, Annals of Pure and Applied Logic, vol. 110 (2001), pp. 107–234.Google Scholar
[5] Tarski, A., On well-ordered subsets of any set, Fundamenta Mathematicae, vol. 32 (1939), pp. 176–183.Google Scholar
[6] Truss, J. K., Permutations and the axiom of choice, Automorphisms of first-order structures (Kaye, R. and Macpherson, D., editors), Oxford University Press, 1994, pp. 131–152.Google Scholar