Published online by Cambridge University Press: 12 March 2014
For a model 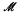 of Peano Arithmetic, let Lt(
of Peano Arithmetic, let Lt(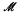 ) be the lattice of its elementary substructures, and let Lt+ (
) be the lattice of its elementary substructures, and let Lt+ (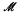 ) be the equivalenced lattice (Lt(
) be the equivalenced lattice (Lt(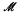 ),≅
),≅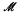 ), where ≅
), where ≅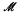 is the equivalence relation of isomorphism on Lt(
is the equivalence relation of isomorphism on Lt(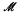 ). It is known that Lt+(
). It is known that Lt+(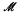 ) is always a reasonable equivalenced lattice.
) is always a reasonable equivalenced lattice.
Theorem. Let L be a finite distributive lattice and let (L, E) be reasonable. If 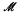 0 is a nonstandard prime model of PA, then
0 is a nonstandard prime model of PA, then 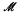 0 has a cofinal extension
0 has a cofinal extension 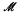 such that Lt+(
such that Lt+(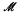 ) ≅ (L,E).
) ≅ (L,E).
A general method for proving such theorems is developed which, hopefully, will be able to be applied to some nondistributive lattices.