Article contents
Nicht konstruktiv beweisbare Sätze der Analysis
Published online by Cambridge University Press: 12 March 2014
Extract
Nach allgemeiner Ueberzeugung können gewisse Sätze der Analysis nicht konstruktiv bewiesen werden. Man denke etwa an den folgenden Satz: Eine monotone und beschränkte Folge a(n) von rationalen Zahlen konvergiert, d.h. es gibt eine solche ganzzahlige Funktion k(m), daß

Unter einem konstruktiven Beweis dieses Satzes hätte man etwa die Angabe eines Verfahrens zu verstehen, das gestattet, die Funktion k(m) auf Grand der Folge a(n) rekursiv zu definieren. Wenn ein solcher Beweis vorläge, wäre insbesondere gezeigt, daß es zu einer rekursiv definierten Folge a(n) mit den verlangten Eigenschaften stets eine rekursiv definierbare Konvergenzfunktion k(m) gibt.
Es soil nun im folgenden von einigen grundlegenden Sätzen der reellen Analysis gezeigt werden, daß sie nicht konstruktiv bewiesen werden können—konstruktiv in dem Sinn, der eben angedeutet wurde. Wir stützen uns dabei auf die Begriffe der rekursiven und der berechenbaren Funktion; rekursive und berechenbare Funktionen sind zahlentheoretische Funktionen. Unter einer rekursiven Funktion möge vorläufig eine primitiv rekursive Funktion verstanden werden (vgl. etwa D. Hilbert und P. Bernays [3], S.286); berechenbar meint berechenbar im Sinne von A. Church [1], S. C. Kleene [4], A. M. Turing [6]. Der Begriff der “konstruktiv definierten Funktion” wird durch die Bestimmung als “rekursive Funktion” eher eng, durch die Bestimmung als “berechenbare Funktion” eher weit gefaßt.
Definition I. Eine Folge rationaler Zahlen Φ(n) heißt rekursiv,(berechenbar), wenn es solche rekursiven (berechenbaren) Funktionen ϕ{n), ψ(n) und χ(n) gibt, daß χ(n) ≧1 und
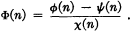 .
.
Definition II. Eine Folge Φ(n) von rationalen Zahlen heißt rekursiv (berechenbar) konvergent, wenn es eine solche rekursive (berechenbare) Funktion v(m) gibt, daß

Wir werden zeigen (Satz I): Es gibt eine rekursive, monotone und beschränkte Folge rationaler Zahlen, die nicht berechenbar konvergiert. Bei unserer Auffassungsweise ist darin enthalten, daß der zu Beginn erwähnte Satz nicht konstruktiv bewiesen werden kann.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1949
References
Literatur
- 211
- Cited by


