Article contents
A new version of Beth semantics for intuitionistic logic
Published online by Cambridge University Press: 12 March 2014
Extract
We use the notation of Kripke's paper [1]. Let M = (G, K, R) be a tree structure and D a domain and η a Beth model on M. The truth conditions of the Beth semantics for ∨ and ∃ are (see [1]):
(a) η (A ∨ B, H) = T iff for some B ⊆ K, B bars H and for each H′ ∈ B, either η(A, H′) = T or η(B, H′) = T.
(b) η(∃xA(x), H) = T iff for some B ⊆ K, B bars H and for each H′ ∈ B there exists an a ∈ D such that η(A (a), H′) = T.
Suppose we change the truth definition η to η* by replacing condition (b) by the condition (b*) (well known from the Kripke interpretation):
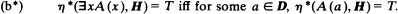
Call this type of interpretation the new version of Beth semantics. We prove
Theorem 1. Intuitionistic predicate logic is complete for the new version of the Beth semantics.
Since Beth structures are of constant domains, and in the new version of Beth semantics the truth conditions for ∧, →, ∃, ∀, ¬ are the same as for the Kripke interpretation, we get:
Corollary 2. The fragment without disjunction of the logic CD of constant domains (i.e. with the additional schema ∀x(A ∨ B(x))→ A ∨ ∀xB(x), x not free in A) equals the fragment without disjunction of intuitionistice logic.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1977
References
REFERENCES
- 2
- Cited by


