Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T11:29:12.358Z Has data issue: false hasContentIssue false
  • English
  • Français

A new “feasible” arithmetic

Published online by Cambridge University Press:  12 March 2014

Stephen Bellantoni  and
Martin Hofmann
Stephen Bellantoni
Affiliation:
Department of Computer Science, University of Toronto, Toronto, Canada, E-mail: [email protected]
Martin Hofmann
Affiliation:
Laboratory for Foundations of Computer Science, University of Edinburgh, Edinburgh, Scotland, UK, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A classical quantified modal logic is used to define a “feasible” arithmetic 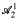whose provably total functions are exactly the polynomial-time computable functions. Informally, one understands ⃞∝ as “∝ is feasibly demonstrable”.

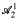differs from a system that is as powerful as Peano Arithmetic only by the restriction of induction to ontic (i.e., ⃞-free) formulas. Thus, 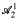is defined without any reference to bounding terms, and admitting induction over formulas having arbitrarily many alternations of unbounded quantifiers. The system also uses only a very small set of initial functions.

To obtain the characterization, one extends the Curry-Howard isomorphism to include modal operations. This leads to a realizability translation based on recent results in higher-type ramified recursion. The fact that induction formulas are not restricted in their logical complexity, allows one to use the Friedman A translation directly.

The development also leads us to propose a new Frege rule, the “Modal Extension” rule: if ⊢ ∝ a then ⊢ A↔ ∝ for new symbol A.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 1 , March 2002 , pp. 104 - 116
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abramsky, S., Computational interpretations of linear logic, Theoretical Computer Science, vol. 111 (1993), pp. 3–57.CrossRefGoogle Scholar
[2]Bellantoni, S., Ranking arithmetic proofs by implicit ramification, Proof complexity and feasible arithmetics (Beame, P. and Buss, S., editors), DIMACS Series in Discrete Mathematics, vol. 39, 1998.Google Scholar
[3]Bellantoni, S. and Cook, S., A new recursion-theoretic characterization of the polytime functions, Computational Complexity, vol. 2 (1992), pp. 97–110.CrossRefGoogle Scholar
[4]Bellantoni, S. and Niggl, K. H., Ranking recursions: the low Grzegorczyk hierarchy reconsidered, SIAM Journal of Computing, (to appear).Google Scholar
[5]Bellantoni, S., Niggl, K. H., and Schwichtenberg, H., Ramification, modality, and linearity in higher type recursion, Annals of Pure and Applied Logic, (2000).Google Scholar
[6]Boolos, G. and Sambin, G., Provability: the emergence of a mathematical modality, Studia Logica, vol. 1 (1991), pp. 1–23.CrossRefGoogle Scholar
[7]Buss, S., Bounded arithmetic, Bibliopolis, Naples, 1986.Google Scholar
[8]Coquand, T., Computational content of classical proofs, Semantics and logics of computation (Pitts, A. and Dybjer, P., editors), Cambridge University Press, 1997.Google Scholar
[9]Girard, J. Y., Light linear logic, vol. 143 (1998).Google Scholar
[10]Girard, J. Y., Scedrov, A., and Scott, P. J., Bounded linear logic: a modular approach to polynomial-time computability, Theoretical Computer Science, vol. 97 (1992), pp. 1–66.CrossRefGoogle Scholar
[11]Goodman, N., Epistemic arithmetic is a conservative extension of intuitionistic arithmetic, this Journal, vol. 49 (1984), no. 1.Google Scholar
[12]Hofmann, M., A mixed modal/linear lambda calculus with applications to Bellantoni-Cook safe recursion, CSL '97, Springer Lecture Notes in Computer Science, vol. 1414, 1998, pp. 275–294.Google Scholar
[13]Hofmann, M., Type systems for polynomial-time computation, Technical report, Darmstadt University of Technology, 1999, Available as Edinburgh University LFCS Technical Report ECS-LFCS-99-406 or via www.dcs.ed.ac.uk/home/mxh/.Google Scholar
[14]Hofmann, M., Safe recursion with higher types and BCK-algebras, Annals of Pure and Applied Logic, vol. 104 (2000), pp. 113–166.CrossRefGoogle Scholar
[15]Immerman, N., Languages that capture complexity classes, SIAM Journal of Computing, vol. 4 (1987), no. 16.Google Scholar
[16]Krajicek, J., Bounded arithmetic, prepositional logic, and complexity theory, Cambridge University Press, 1995.CrossRefGoogle Scholar
[17]Leivant, D., Ramified recurrence and computational complexity I: Word recurrence and poly-time, Feasible mathematics II (Clote, P. and Remmel, J., editors), Perspectives in Computer Science, Birkhauser, 1994, pp. 320–343.Google Scholar
[18]Leivant, D., Intrinsic theories and computational complexity, Logic and computational complexity, international workshop LCC '94, Indianapolis (Leivant, D., editor), Lecture Notes in Computer Science, vol. 960, Springer, 1995, pp. 177–194.CrossRefGoogle Scholar
[19]Leivant, D. and Marion, J. Y., Ramified recurrence and computational complexity IV: Predicative functionals and poly-space, Information and Computation, (to appear).Google Scholar
[20]Nelson, E., Predicative arithmetic, Princeton University Press, Princeton, NJ, 1986.CrossRefGoogle Scholar
[21]Nelson, E., Ramified recursion and intuitionism, Princeton University, 1997, manuscript.Google Scholar
[22]Nelson, E., Understanding intuitionism, Rencontre du reseau georges reeb, 03 24-28 1997.Google Scholar
[23]Shapiro, S., Epistemic and intuitionistic arithmetic, Intensional mathematics (Shapiro, S., editor), Studies in Logic and The Foundations of Mathematics, vol. 113, North-Holland, 1985.Google Scholar
[24]Simmons, H., The realm of primitive recursion, Archive for Mathematical Logic, vol. 27 (1988), pp. 177+.CrossRefGoogle Scholar
[25]Troelstra, A. S. and van Dalen, D., Constructivism in mathematics, volume I, North-Holland, 1988.Google Scholar