Article contents
A new approach to semantics – Part II1
Published online by Cambridge University Press: 12 March 2014
Extract
I will give precise versions of the foregoing verbal definitions, by formalizing them within a formal metalanguage.
In order to avoid the necessity of formulating a meta-language, I will make use of VI 112, (i.e., Gödel's The consistency of the continuum hypothesis). Actually, the system there developed is unnecessarily strong for the limited purpose of this illustration. It will suffice to choose for 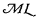 the system of VI 112 without axioms C4 and E (axioms of replacement and choice); this system will be the logical basis of
the system of VI 112 without axioms C4 and E (axioms of replacement and choice); this system will be the logical basis of 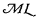 , and to this I will add some set-constants and some meaning postulates. The logical basis is roughly as strong as Zermelo's system with an axiom of infinity.
, and to this I will add some set-constants and some meaning postulates. The logical basis is roughly as strong as Zermelo's system with an axiom of infinity.
Within 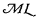 I will set up analogues of the previous definitions, applicable to a wide variety of object-languages. For the sake of concreteness it will be convenient to think of
I will set up analogues of the previous definitions, applicable to a wide variety of object-languages. For the sake of concreteness it will be convenient to think of 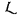 as having Zermelo set theory, without the axiom of infinity, as its logical basis – but it must be kept in mind that this is not an essential feature of the forthcoming definitions.
as having Zermelo set theory, without the axiom of infinity, as its logical basis – but it must be kept in mind that this is not an essential feature of the forthcoming definitions.
Our 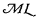 is certainly strong enough to have all primitive recursive functions calculable within it. This supplies us with the needed tool for talking about
is certainly strong enough to have all primitive recursive functions calculable within it. This supplies us with the needed tool for talking about 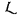 , within
, within 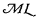 , by introducing a number of primitive recursive functions, properties, and relations describing the structure of
, by introducing a number of primitive recursive functions, properties, and relations describing the structure of 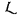 . The exact definitions of these will depend on the exact form of
. The exact definitions of these will depend on the exact form of 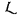 , but for the forthcoming definitions it will suffice to know that these functions, properties, and relations are representable in
, but for the forthcoming definitions it will suffice to know that these functions, properties, and relations are representable in 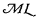 for the given
for the given 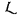 . This makes the resulting definitions most useful, since they can be applied to any
. This makes the resulting definitions most useful, since they can be applied to any 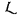 of the type described.
of the type described.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1956
Footnotes
Part I appeared in this Journal, vol. XXI, pp. 1–27.
References
3 By the results of I. Novak and A. Mostowski we know that the Zermelo system is equivalent to VI 112 without axioms C4 and E.
4 See, e.g., chapter X of XIX 215.
5 These functions, properties, and relations are defined with reference to ![]() , but they are defined in
, but they are defined in ![]() .
.
6 This is not a primitive recursive property, but it is here listed because it is easily definable in terms of primitive recursive relations.
7 It is important to recall that a phrase is a special formula without free variables. The semantic definitions are applied to phrases.
8 Cf. XIII 220.
9 It must be recalled that 2 = {0, 1}.
10 In general the value of a special formula depends on the assignment to the free variables, but phrases have no free variables.
11 Other semantic concepts can be defined just as easily.
12 I hope to consider such proofs for a variety of systems in a future paper.
13 18 = 2132, hence ‘18’ is the number of (οι). 1 × d is a function having d as domain and being identically equal to 0.
14 A property will be treated as a unary relation.
15 The convention adopted in Part I is that formulas of ![]() serve as names of themselves, but formulas of
serve as names of themselves, but formulas of ![]() are put between quotation marks to avoid confusion.
are put between quotation marks to avoid confusion.
16 The names of semantic relations will be capitalized to call attention to them.
17 Translations were actually introduced for all wffs, but only sentences are phrases.
18 The condition was introduced by Carnap as a condition of adequacy for L-truth in VIII 36 (D16–1). I have replaced L-truth by Atrueness.
19 For every semantic theorem of ![]() concerning
concerning ![]() we can prove two theorems in
we can prove two theorems in ![]() . We can prove the translation of the theorem and we can prove an analogous theorem concerning
. We can prove the translation of the theorem and we can prove an analogous theorem concerning ![]() .
.
20 See the discussion of translations at the beginning of this section.
21 The translation of “Atrue(A)” is that Atrue(A) in ![]() .
.
22 The argument is simplified here by ignoring meaning postulates.
23 This distinction can be made especially clear in terms of XVII 133. Two phrases are synonymous if they have the same sense. If “same sense” is taken according to Church's alternative 2, we get weak synonymy, corresponding to free translation. Church's alternative 0 gives us a strong concept of synonymy, corresponding to literal translation.
24 Cf. Part I, section 5.
- 6
- Cited by


