No CrossRef data available.
Article contents
MOST(?) THEORIES HAVE BOREL COMPLETE REDUCTS
Published online by Cambridge University Press: 27 September 2021
Abstract
We prove that many seemingly simple theories have Borel complete reducts. Specifically, if a countable theory has uncountably many complete one-types, then it has a Borel complete reduct. Similarly, if
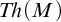 $Th(M)$
is not small, then
$Th(M)$
is not small, then
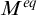 $M^{eq}$
has a Borel complete reduct, and if a theory T is not
$M^{eq}$
has a Borel complete reduct, and if a theory T is not
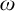 $\omega $
-stable, then the elementary diagram of some countable model of T has a Borel complete reduct.
$\omega $
-stable, then the elementary diagram of some countable model of T has a Borel complete reduct.
MSC classification
Secondary:
03E15: Descriptive set theory
- Type
- Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
Friedman, H. and Stanley, L., A Borel reducibility theory for classes of countable structures, this Journal, vol. 54 (1989), no. 3, pp. 894–914.Google Scholar
Gao, S., Invariant Descriptive Set Theory, Chapman & Hall/CRC Pure and Applied Mathematics, vol. 293, CRC Press, Boca Raton, 2008.CrossRefGoogle Scholar
Kechris, A., Classical Descriptive Set Theory, Graduate Texts in Mathematics, vol. 156, Springer, New York, 1995.CrossRefGoogle Scholar
Laskowski, M. C., Mutually algebraic structures and expansions by predicates, this Journal, vol. 78 (2013), no. 1, pp. 185–194.Google Scholar
Laskowski, M. C. and Shelah, S., Borel complexity of some
 ${\aleph}_0$
-stable theories
. Fundamenta Mathematicae, vol. 229 (2015), no. 1, pp. 1–46.CrossRefGoogle Scholar
${\aleph}_0$
-stable theories
. Fundamenta Mathematicae, vol. 229 (2015), no. 1, pp. 1–46.CrossRefGoogle Scholar
Laskowski, M. C. and Ulrich, D. S., Characterizing the existence of a Borel complete expansion, submitted, arXiv:2109.06140.Google Scholar
Ulrich, D., Rast, R. and Laskowski, M. C., Borel complexity and potential canonical Scott sentences
. Fundamenta Mathematicae, vol. 239 (2017), no. 2, pp. 101–147.CrossRefGoogle Scholar



