Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-16T01:19:55.281Z Has data issue: false hasContentIssue false
  • English
  • Français

A modified sentence unprovable in PA

Published online by Cambridge University Press:  12 March 2014

L. Gordeev
L. Gordeev*
Affiliation:
WSI fur Informatik, Mathematische Logik, Universitat Tubingen, D-72076 Tubingen, Germany, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

H. Friedman proved that the following sentence SWQO(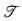) is true but not provable in the theory ATR0 (cf. [S]; 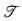≔ the set of finite rooted trees, ∣T∣ ≔ the cardinality of T ∈ ).

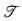For every k > 0 there is an n so large that for any T0, T1,…, Tn ∈ 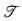with ∀i ≤ n(∣Ti∣ ≤ k · (i + 1)) there are i < j ≤ n such that Ti is homeomorphically embeddable into Tj.

Since ATR0 is stronger than PA, SWQO(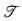) is not provable in PA, either. Furthermore, SWQO(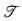) is proof-theoretically stronger than PA. A similar sentence whose proof-theoretical strength is exactly that of PA was obtained by replacing finite trees by finite sequences of bounded natural numbers under the embeddability with H. Friedman's asymmetrical gap-condition (see [SS]). The latter sentence was modified by using the weaker symmetrical gap-condition (see the corresponding particular case in [Gl]). Further improvement is indicated in [G2, Corollary 4.5]. Namely, the assertion ∣Xi∣ ≤ k · (i + 1) as in SWQO(J), above, can be weakened to

.

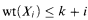(in fact, to wt(Xi) ≤ k + ε · i for an arbitrary fixed ε = l−1, l < 0, where wt(X) is the weight of the “word” X).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 4 , December 1994 , pp. 1154 - 1157
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[G1]Gordeev, L., Generalizations of the one-dimensional version of the Kruskal-Friedman theorems, this Journal, vol. 54 (1989), pp. 100–121.Google Scholar
[G2]Gordeev, L., Quasi-ordinuls and proof theory, Graph structure theory (Robertson, N. and Seymour, P., editors), Contemporary Mathematics, vol. 147, American Mathematical Society, Providence, Rhode Island, 1993, pp. 485–494.CrossRefGoogle Scholar
[PH]Paris, J. and Harrington, L., A mathematical imcompleteness in Peano arithmetic, Handbook of mathematical logic, North-Holland, Amsterdam, 1977, pp. 1133–1142.CrossRefGoogle Scholar
[PK]Paris, J. and Kirby, L., Accessible independence results for Peano arithmetic, Bulletin of the London Mathematical Society, vol. 14 (1982), pp. 285–293.Google Scholar
[S]Simpson, S., Nonprovahility of certain combinatorial properties of finite trees, Harvey Friedman's research on the foundations of mathematics, North-Holland, Amsterdam, 1985, pp. 87–117.CrossRefGoogle Scholar
[SS]Schütte, K. and Simpson, S., Ein in der reinen Zahlentheorie unbeweisbarer Satz über endliche Folgen von natürlichen Zahlen, Archiv für Mathematische Logik und Grundlagenforschung, vol. 25 (1985), pp. 75–89.CrossRefGoogle Scholar
[T]Takeuti, G., Proof theory, 2nd ed., North-Holland, Amsterdam, 1987.Google Scholar