Article contents
Models of set theory with more real numbers than ordinals
Published online by Cambridge University Press: 12 March 2014
Extract
Suppose M is a countable standard transitive model of set theory. P. J. Cohen [2] showed that if κ is an infinite cardinal of M then there is a one-to-one function Fκ from κ into the set of real numbers such that M[Fκ] is a model of set theory with the same cardinals as M.
If Tκ is the range of Fκ then Cohen also showed [2] that M[Tκ] fails to satisfy the axiom of choice. We will give an easy proof of this fact.
If κ, λ are infinite we will also show that M[Tκ] is elementarily equivalent to M[Tλ] and that (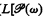 ] in M[Fλ]) is elementarily equivalent to (
] in M[Fλ]) is elementarily equivalent to (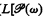 ] in M[FK]).
] in M[FK]).
Finally we show that there may be an N ∈ M[GK] which is a standard model of set theory (without the axiom of choice) and which has, from the viewpoint of M[GK], more real numbers than ordinals.
We write ZFC and ZF for Zermelo-Fraenkel set theory, respectively with and without the axiom of choice (AC). GBC is Gödel-Bernays' set theory with AC. DC and ACℵo are respectively the axioms of dependent choice and of countable choice defined in [6].
Lower case Greek characters (other than ω) are used as variables over ordinals. When α is an ordinal, R(α) is the set of all sets with rank less than α.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1974
References
BIBLIOGRAPHY
- 2
- Cited by


