Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T11:57:31.438Z Has data issue: false hasContentIssue false
  • English
  • Français

Model theoretic connected components of finitely generated nilpotent groups

Published online by Cambridge University Press:  12 March 2014

Nathan Bowler ,
Cong Chen  and
Jakub Gismatullin
Nathan Bowler
Affiliation:
Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, United Kingdom.E-mail:[email protected]
Cong Chen
Affiliation:
School of Mathematics, University of Leeds, Woodhouse Lane, Leeds, LS2 9JT, UK, E-mail: [email protected]
Jakub Gismatullin
Affiliation:
School of Mathematics, University of Leeds, Woodhouse Lane, Leeds, LS2 9JT, UK Instytut Matematyczny Uniwersytetu Wrocławskiego, Pl. Grunwaldzki 2/4, 50-384 Wrocław, Poland, E-mail: [email protected] URL: www.math.uni.wroc.pl/~gismat
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that for a finitely generated infinite nilpotent group G with structure (G, ·, …), the connected component G*0 of a sufficiently saturated extension G* of G exists and equals

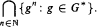
We construct an expansion of ℤ by a predicate (ℤ, +, P) such that the type-connected component 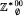is strictly smaller than ℤ*0. We generalize this to finitely generated virtually solvable groups. As a corollary of our construction we obtain an optimality result for the van der Waerden theorem for finite partitions of groups.

Keywords

model theoretic connected componentsfinitely generated groupthick setvan der Waerden theorem
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 78 , Issue 1 , March 2013 , pp. 245 - 259
Copyright
Copyright © Association for Symbolic Logic 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Casanovas, E., Lascar, D., Pillay, A., and Ziegler, M., Galois groups of first order theories, Journal of Mathematical Logic, vol. 1 (2001), pp. 305–319.CrossRefGoogle Scholar
[2]Gismatullin, J., Absolute connectedness and classical groups, 2011, preprint, arXiv: 1002.1516.Google Scholar
[3]Gismatullin, J., Model theoretic connected components of groups, Israel Journal of Mathematics, vol. 184 (2011), pp. 251–274.CrossRefGoogle Scholar
[4]Gismatullin, J. and Newelski, L., G-compactness and groups, Archive for Mathematical Logic, vol. 47 (2008), pp. 479–501.CrossRefGoogle Scholar
[5]Graham, R. L., Rothschild, B. L., and Spencer, J. H., Ramsey theory, second ed., John Wiley & Sons, Inc., New York, 1990.Google Scholar
[6]Hrushovski, E., Kropholler, P. H., Lubotzky, A., and Shalev, A., Powers in finitely generated groups, Transactions of the American Mathematical Society, vol. 348 (1996), pp. 291–304.CrossRefGoogle Scholar
[7]Kargapolov, M. I. and Merzljakov, Ju. I., Fundamentals of the theory of groups, Graduate Texts in Mathematics, 62, Springer-Verlag, New York-Berlin, 1979.CrossRefGoogle Scholar
[8]Mal'cev, A. I., On homomorphisms onto finite groups, Uchenye zapiski Ivanovslcogo pedagogicheskogo instituta, vol. 18 (1958), pp. 49–60, English translation in Twelve papers in algebra, (Lev J. Leifman, editor), American Mathematical Society Translations, Series 2, 119. American Mathematical Society, Providence, R.I., 1983, pp. 67–79.Google Scholar
[9]Marker, D., Model theory, Graduate Texts in Mathematics, 217, Springer-Verlag, New York, 2002.Google Scholar
[10]Martinez, C., On power subgroups of profinite groups, Transactions of the American Mathematical Society, vol. 345 (1994), pp. 865–869.CrossRefGoogle Scholar
[11]Miller, C., Expansions of dense linear orders with the intermediate value property, this Journal, vol. 66 (2001), no. 4, pp. 1783–1790.Google Scholar
[12]Pillay, A., Type-definability, compact Lie groups, and o-minimality, Journal of Mathematical Logic, vol. 4 (2004), pp. 147–162.CrossRefGoogle Scholar