Model existence theorems for modal and intuitionistic logics

Extract

In classical logic a collection of sets of statements (or equivalently, a property of sets of statements) is called a consistency property if it meets certain simple closure conditions (a definition is given in §2). The simplest example of a consistency property is the collection of all consistent sets in some formal system for classical logic. The Model Existence Theorem then says that any member of a consistency property is satisfiable in a countable domain. From this theorem many basic results of classical logic follow rather simply: completeness theorems, the compactness theorem, the Lowenheim-Skolem theorem, and the Craig interpolation lemma among others. The central position of the theorem in classical logic is obvious. For the infinitary logic 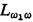the Model Existence Theorem is even more basic as the compactness theorem is not available; [8] is largely based on it.

In this paper we define appropriate notions of consistency properties for the first-order modal logics S4, T and K (without the Barcan formula) and for intuitionistic logic. Indeed we define two versions for intuitionistic logic, one deriving from the work of Gentzen, one from Beth; both have their uses. Model Existence Theorems are proved, from which the usual known basic results follow. We remark that Craig interpolation lemmas have been proved model theoretically for these logics by Gabbay ([5], [6]) using ultraproducts. The existence of both ultra-product and consistency property proofs of the same result is a common phenomena in classical and infinitary logic. We also present extremely simple tableau proof systems for S4, T, K and intuitionistic logics, systems whose completeness is an easy consequence of the Model Existence Theorems.