Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T05:47:50.053Z Has data issue: false hasContentIssue false
  • English
  • Français

Model companions of distributive p-algebras

Published online by Cambridge University Press:  12 March 2014

Jürg Schmid
Jürg Schmid*
Affiliation:
Universität Bern, Bern, Switzerland
Get access Rights & Permissions [Opens in a new window]

Extract

Let Bn, 0 ≤ n ≤ ω, be the equational classes of distributive p-algebras (precise definitions are given in §1). It has been known for some time that the elementary theories Tn of Bn possess model companions 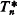; see, e.g., [6] and [14] and the references given there. However, no axiomatizations of 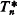were given, with the exception of n = 0 (Boolean case) and n= 1 (Stonian case). While the first case belongs to the folklore of the subject (see [6], also [11]), the second case presented considerable difficulties (see Schmitt [13]). Schmitt's use of methods characteristic for Stone algebras seems to prevent a ready adaptation of his results to the cases n ≥ 2.

The natural way to get a hold on 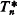is to determine the class E(Bn) of existentially complete members of Bn: Since 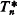exists, it equals the elementary theory of E(Bn). The present author succeeded [12] in solving the simpler problem of determining the classes A(Bn) of algebraically closed algebras in Bn (exact definitions of A(Bn) and E(Bn) are given in §1) for all 0 > n < ω. A(Bn) is easier to handle since it contains sufficiently many “small” algebras-viz. finite direct products of certain subdirectly irreducibles-in terms of which the members of A(Bn) may be analyzed (in contrast, all members of E(Bn) are infinite and ℵ-homogeneous). As it turns out, A(Bn) is finitely axiomatizable for all n, and comparing the theories of A(B0), A(B1) with the explicitly known theories of E(B0), E(B1)-viz. 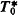, , 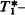a reasonable conjecture for 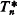, 2 ≤ n ≤ ω, is immediate. The main part of this paper is concerned with verifying that the conditions formalized by 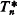suffice to describe the algebras in E(Bn) (necessity is easy). This verification rests on the same combinatorial techniques as used in [12] to describe the members of A(Bn).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 47 , Issue 3 , September 1982 , pp. 680 - 688
Copyright
Copyright © Association for Symbolic Logic 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Burris, S., An existence theorem for model companions, Proceedings of the Ulm Lattice Theory Conference (Kalmbach, G., Editor), Ulm, 1975, pp. 33–37.Google Scholar
[2] Eklof, P. and Sabbagh, G., Model completions and modules, Annals of Mathematical Logic, vol. 2 (1970), pp. 251–295.CrossRefGoogle Scholar
[3] Grätzer, G., Lattice theory: First concepts and distributive lattices, Freeman, San Francisco, 1971.Google Scholar
[4] Grätzer, G. and Lakser, H., The structure of pseudocomplemented distributive lattices. II: Congruence extension and amalgamation, Transactions of the American Mathematical Society, vol. 156 (1971), pp. 343–357.Google Scholar
[5] Grätzer, G. and Lakser, H., The structure of pseudocomplemented distributive lattices. III: Injective and absolute subretracts, Transactions of the American Mathematical Society, vol. 169 (1972), pp. 475–487.Google Scholar
[6] Hirschfeld, J. and Wheeler, W. H., Forcing, arithmetic, division rings, Lecture Notes in Mathematics, vol. 454, Springer-Verlag, Berlin and New York, 1975.Google Scholar
[7] Katriňák, T., Subdirectly irreducible modular p-algebras, Algebra Universalis, vol. 2 (1972), pp. 166–173.CrossRefGoogle Scholar
[8] Katriňák, T., Ueber eine Konstruktion der distributiven pseudokomplementären Verbände, Mathematische Nachrichten, vol. 53 (1972), pp. 85–99.CrossRefGoogle Scholar
[9] Katriňák, T., Die Kennzeichnung der distributiven pseudokomplementären Halbverbände, Journal für die Reine und Angewandte Mathematik, vol. 241 (1970), pp. 160–179.Google Scholar
[10] Lee, K. B., Equational classes of distributive pseudo-complemented lattices, Canadian Journal of Mathematics, vol. 22(1970), pp. 881–891.CrossRefGoogle Scholar
[11] Schmid, J., Algebraically and existentially closed distributive lattices, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 25 (1979), pp. 525–530.CrossRefGoogle Scholar
[12] Schmid, J., Algebraically closed distributive p-algebras, Algebra Universalis (to appear).Google Scholar
[13] Schmitt, P.H., The model completion of Stone algebras, Annales Scientifiques de VUniver-sité de Clermont, Série Mathématique, fasc. 13 (1976), pp. 135–155.Google Scholar
[14] Weispfenning, V., A note on ℵ0-categorical model companions, Archiv für Mathematische Logik und Grundlagenforschung, vol. 19(1978), pp. 23–29.CrossRefGoogle Scholar