Article contents
Minimal upper bounds for sequences of 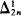 -degrees
-degrees
Published online by Cambridge University Press: 12 March 2014
Extract
It is proved here, assuming Projective Determinacy, that every ascending sequence of 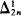 -degrees has a minimal strict upper bound but no least strict upper bound. This generalizes a result of Friedman for n = 1.
-degrees has a minimal strict upper bound but no least strict upper bound. This generalizes a result of Friedman for n = 1.
Our general notation and terminology will be that of [Ke1] and [Mo1]. Letters i,j, k,… denote members of ω and α, β, ϒ,… members of ωω i.e. reals. Projective Determinacy (PD) is the hypothesis that every projective set of reals in determined, while in general for a collection of sets of reals Γ, Determinacy (Γ) abbreviates the statement that every set in Γ is determined.
§1. 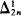 -degrees. For each m ≥ 1 and α, β Є ωω let α ≤mβ ⇔ α Є
-degrees. For each m ≥ 1 and α, β Є ωω let α ≤mβ ⇔ α Є 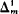 (β), α <mβ ⇔ α ≤mβ ∧ β ≰mα, and α ≡mβ ⇔ α ≤mβ ∧ β ≤mα.Clearly ≡m is an equivalence relation on ωω. The ≡m -equivalence class of α Є ωω is called its
(β), α <mβ ⇔ α ≤mβ ∧ β ≰mα, and α ≡mβ ⇔ α ≤mβ ∧ β ≤mα.Clearly ≡m is an equivalence relation on ωω. The ≡m -equivalence class of α Є ωω is called its 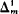 -degree, in symbols
-degree, in symbols
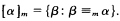
If d = [α]m, e = [β]m then we define

- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1978
References
REFERENCES
- 1
- Cited by


