Article contents
Minimal upper bounds for ascending sequences of α-recursively enumerable degrees
Published online by Cambridge University Press: 12 March 2014
Extract
Let a be an admissible ordinal and let ∧ ≤ α be a limit ordinal. A sequence of a-r.e. degrees 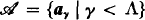 is said to be ascending, simultaneous and of length ∧ if (i) there is an α-recursive function t: α × ∧ → α such that, for all ϒ < ∧, A
ϒ = {t(σ, ϒ)∣ σ < α} is of degree a
ϒ; (ii) if ϒ < ⊤ < ∧, then a
ϒ ≤α
a
τ and (iii) for all ϒ < ∧, there is a ⊤ > ϒ with a
ϒ, >α
a
ϒ. Lerman [4] showed that such an
is said to be ascending, simultaneous and of length ∧ if (i) there is an α-recursive function t: α × ∧ → α such that, for all ϒ < ∧, A
ϒ = {t(σ, ϒ)∣ σ < α} is of degree a
ϒ; (ii) if ϒ < ⊤ < ∧, then a
ϒ ≤α
a
τ and (iii) for all ϒ < ∧, there is a ⊤ > ϒ with a
ϒ, >α
a
ϒ. Lerman [4] showed that such an 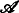 exists for every ∧ ≤ α. An upper bound a of
exists for every ∧ ≤ α. An upper bound a of 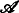 is an α-r.e. degree in which every element of
is an α-r.e. degree in which every element of 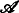 is α-recursive. a is minimal if there is no α-r.e. degree b <α
a which is also an upper bound of
is α-recursive. a is minimal if there is no α-r.e. degree b <α
a which is also an upper bound of 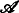 . Sacks [6] proved that every ascending sequence of simultaneously ω-r.e. degrees of length ω cannot have 0ω′, the complete ω-r.e. degree, as a minimal upper bound. In contrast, Cooper [2] showed that there exists an ascending sequence of simultaneously ω-r.e. degrees of length to having a minimal upper bound which is an ω-r.e. degree. In this paper we investigate the behavior of ascending sequences of simultaneously α-r.e. degrees for admissible ordinals α > ω. Call α Σ∞-admissibIe if it is Σ
n
-nadmissible for all n. Let Φ(∧) say: No ascending sequence of simultaneously α-r.e. degrees of length ∧ can have 0α′, the complete α-r.e. degree, as a minimal upper bound. Our main result in this paper is:
. Sacks [6] proved that every ascending sequence of simultaneously ω-r.e. degrees of length ω cannot have 0ω′, the complete ω-r.e. degree, as a minimal upper bound. In contrast, Cooper [2] showed that there exists an ascending sequence of simultaneously ω-r.e. degrees of length to having a minimal upper bound which is an ω-r.e. degree. In this paper we investigate the behavior of ascending sequences of simultaneously α-r.e. degrees for admissible ordinals α > ω. Call α Σ∞-admissibIe if it is Σ
n
-nadmissible for all n. Let Φ(∧) say: No ascending sequence of simultaneously α-r.e. degrees of length ∧ can have 0α′, the complete α-r.e. degree, as a minimal upper bound. Our main result in this paper is:
Let α be either a constructible cardinal with σ2ci(α) < α or Σ∞-admissible. Then σ2cf(α) is the least ordinal ν for which every ∧ ≤ α of cofinality ν (over L α) can satisfy Φ(∧).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1976
References
BIBLIOGRAPHY
- 1
- Cited by


