Article contents
Minimal pairs and high recursively enumerable degrees
Published online by Cambridge University Press: 12 March 2014
Extract
A. H. Lachlan [2] and C. E. M. Yates [4] independently showed that minimal pairs of recursively enumerable (r.e.) degrees exist. Lachlan and Richard Ladner have shown (unpublished) that there is no uniform method for producing a minimal pair of r.e. degrees below a given nonzero r.e. degree. It is not known whether every nonzero r.e. degree bounds a r.e. minimal pair, but in the present paper it is shown (uniformly) that every high r.e. degree bounds a r.e. minimal pair. (A r.e. degree is said to be high if it contains a high set in the sense of Robert W. Robinson [3].)
Theorem. Let a be a recursively enumerable degree for which a′ = 0″. Then there are recursively enumerable degrees b0 and b1 such that0 < bi < a for each i ≤ 1, and b0 ⋂ b1 = 0.
The proof is based on the Lachlan minimal r.e. pair construction. For notation see Lachlan [2] or S. B. Cooper [1].
By Robinson [3] we can choose a r.e. representative A of the degree a, with uniformly recursive tower {As, ∣ s ≥ 0} of finite approximations to A, such that CA dominates every recursive function where
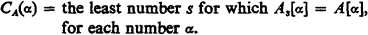
We define, stage by stage, finite sets Bi,s, i ≤ 1, s ≥ 0, in such a way that Bi, s + 1 ⊇ Bi,s for each i, s, and {Bi,s ∣ i ≤ 1, s ≥ 0} is uniformly recursive.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1974
References
REFERENCES
- 39
- Cited by


