Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T22:35:25.721Z Has data issue: false hasContentIssue false
  • English
  • Français

MEAGER-ADDITIVE SETS IN TOPOLOGICAL GROUPS

Part of: Locally compact abelian groups Topological and differentiable algebraic systems Set theory

Published online by Cambridge University Press:  27 September 2021

ONDŘEJ ZINDULKA
ONDŘEJ ZINDULKA*
Affiliation:
DEPARTMENT OF MATHEMATICS FACULTY OF CIVIL ENGINEERING CZECH TECHNICAL UNIVERSITY THÁKUROVA 7, 160 00 PRAGUE 6, CZECH REPUBLICE-mail:[email protected]: http://mat.fsv.cvut.cz/zindulka
Get access Rights & Permissions [Opens in a new window]

Abstract

By the Galvin–Mycielski–Solovay theorem, a subset X of the line has Borel’s strong measure zero if and only if 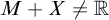$M+X\neq \mathbb {R}$ for each meager set M.

A set 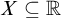$X\subseteq \mathbb {R}$ is meager-additive if 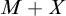$M+X$ is meager for each meager set M. Recently a theorem on meager-additive sets that perfectly parallels the Galvin–Mycielski–Solovay theorem was proven: A set 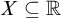$X\subseteq \mathbb {R}$ is meager-additive if and only if it has sharp measure zero, a notion akin to strong measure zero.

We investigate the validity of this result in Polish groups. We prove, e.g., that a set in a locally compact Polish group admitting an invariant metric is meager-additive if and only if it has sharp measure zero. We derive some consequences and calculate some cardinal invariants.

Keywords

Polish groupmeager-additivesharply meager-additivesharp measure zerostrong measure zeroHausdorff measure

MSC classification

Primary: 22B05: General properties and structure of LCA groups
Secondary: 22A10: Analysis on general topological groups 03E17: Cardinal characteristics of the continuum
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 3 , September 2022 , pp. 1046 - 1064
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bartoszyński, T. and Judah, H., Set Theory: On the Structure of the Real Line, A K Peters Ltd., Wellesley, MA, 1995.CrossRefGoogle Scholar
Besicovitch, A. S., Concentrated and rarified sets of points. Acta Mathematica, vol. 62 (1933), no. 1, pp. 289–300.CrossRefGoogle Scholar
Besicovitch, A. S., Correction. Acta Mathematica, vol. 62 (1933), no. 1, pp. 317–318.CrossRefGoogle Scholar
Borel, E., Sur la classification des ensembles de mesure nulle. Bulletin de la Société Mathématique de France, vol. 47 (1919), pp. 97–125.CrossRefGoogle Scholar
Fremlin, D. H., Measure Theory. Volume 5: Set-Theoretic Measure Theory, Torres Fremlin, Colchester, 2008, http://www.essex.ac.uk/maths/people/fremlin/mt5.2008/mt5.2008.tar.gz.Google Scholar
Galvin, F., Mycielski, J., and Solovay, R., Strong measure zero sets, Abstract 79T-E25. Notices of the American Mathematical Society, vol. 26 (1979), p. A-280.Google Scholar
Gerlits, J. and Nagy, Z., Some properties of $C(X)$ . I. Topology and its Applications, vol. 14 (1982), no. 2, pp. 151–161.CrossRefGoogle Scholar
Gödel, K., The Consistency of the Continuum Hypothesis, Annals of Mathematics Studies, vol. 3, Princeton University Press, Princeton, NJ, 1940.CrossRefGoogle Scholar
Hrušák, M., Wohofsky, W., and Zindulka, O., Strong measure zero in separable metric spaces and Polish groups. Archive for Mathematical Logic, vol. 55 (2016), no. 1-2, pp. 105–131.CrossRefGoogle Scholar
Hrušák, M. and Zapletal, J., Strong measure zero sets in Polish groups. Illinois Journal of Mathematics, vol. 60 (2016), nos. 3–4, pp. 751–760.CrossRefGoogle Scholar
Hrušák, M. and Zindulka, O., Strong measure zero in Polish groups , Centenary of the Borel Conjecture (M. Scheepers and O. Zindulka, editors), Contemporary Mathematics, vol. 755, American Mathematical Society, Providence, RI, 2020, pp. 37–68.CrossRefGoogle Scholar
Kysiak, M., On Erdős–Sierpiński duality between Lebesgue measure and Baire category, Master’s thesis, Uniwersytet Warszawski, Warszawa, 2000 (in Polish).Google Scholar
Laver, R., On the consistency of Borel’s conjecture. Acta Mathematica, vol. 137 (1976), nos. 3–4, pp. 151–169.CrossRefGoogle Scholar
Miller, A. W., Some properties of measure and category. Transactions of the American Mathematical Society, vol. 266 (1981), no. 1, pp. 93–114.CrossRefGoogle Scholar
Miller, A. W. and Fremlin, D. H., On some properties of Hurewicz, Menger, and Rothberger. Fundamenta Mathematicae, vol. 129 (1988), no. 1, pp. 17–33.CrossRefGoogle Scholar
Munroe, M. E., Introduction to Measure and Integration, Addison-Wesley Publishing Company, Inc., Cambridge, MA, 1953.Google Scholar
Nowik, A., Scheepers, M., and Weiss, T., The algebraic sum of sets of real numbers with strong measure zero sets, this Journal, vol. 63 (1998), no. 1, pp. 301–324.Google Scholar
Nowik, A. and Weiss, T., On the Ramseyan properties of some special subsets of ${2}^{\unicode{x3c9}}$ and their algebraic sums, this Journal, vol. 67 (2002), no. 2, pp. 547–556.Google Scholar
Pawlikowski, J., Powers of transitive bases of measure and category. Proceedings of the American Mathematical Society, vol. 93 (1985), no. 4, pp. 719–729.CrossRefGoogle Scholar
Pawlikowski, J., A characterization of strong measure zero sets. Israel Journal of Mathematics, vol. 93 (1996), pp. 171–183.CrossRefGoogle Scholar
Prikry, K., unpublished result.Google Scholar
Rogers, C. A., Hausdorff Measures, Cambridge University Press, London, 1970.Google Scholar
Shelah, S., Every null-additive set is meager-additive. Israel Journal of Mathematics, vol. 89 (1995), nos. 1–3, pp. 357–376.CrossRefGoogle Scholar
Sierpiński, W., Sur un ensemble non denombrable, dont toute image continue est de mesure nulle. Fundamenta Mathematicae, vol. 11 (1928), no. 1, pp. 302–304.CrossRefGoogle Scholar
Zakrzewski, P., Universally meager sets. Proceedings of the American Mathematical Society, vol. 129 (2001), no. 6, pp. 1793–1798 (electronic).CrossRefGoogle Scholar
Zakrzewski, P., Universally meager sets. II. Topology and its Applications, vol. 155 (2008), no. 13, pp. 1445–1449.CrossRefGoogle Scholar
Zindulka, O., Universal measure zero, large Hausdorff dimension, and nearly Lipschitz maps. Fundamenta Mathematicae, vol. 218 (2012), no. 2, pp. 95–119.CrossRefGoogle Scholar
Zindulka, O., Strong measure zero and meager-additive sets through the prism of fractal measures. Commentationes Mathematicae Universitatis Carolinae, vol. 60 (2019), no. 1, pp. 131–155.Google Scholar