Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ben-Yaacov, Itay
2005.
Compactness and Independence in Non First Order Frameworks.
Bulletin of Symbolic Logic,
Vol. 11,
Issue. 1,
p.
28.
Poizat, Bruno
and
Yeshkeyev, Aibat
2018.
Positive Jonsson Theories.
Logica Universalis,
Vol. 12,
Issue. 1-2,
p.
101.
Berenstein, Alexander
Hyttinen, Tapani
and
Villaveces, Andrés
2018.
Hilbert spaces with generic predicates.
Revista Colombiana de Matemáticas,
Vol. 52,
Issue. 1,
p.
107.


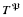 whose saturated models are the lovely pairs of
whose saturated models are the lovely pairs of 