Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T08:29:46.220Z Has data issue: false hasContentIssue false
  • English
  • Français

LINEAR ORDERS REALIZED BY C.E. EQUIVALENCE RELATIONS

Published online by Cambridge University Press:  03 May 2016

EKATERINA FOKINA ,
BAKHADYR KHOUSSAINOV ,
PAVEL SEMUKHIN  and
DANIEL TURETSKY
EKATERINA FOKINA
Affiliation:
KURT GÖDEL RESEARCH CENTER FOR MATHEMATICAL LOGIC UNIVERSITY OF VIENNA VIENNA, AUSTRIAE-mail: [email protected]
BAKHADYR KHOUSSAINOV
Affiliation:
DEPARTMENT OF COMPUTER SCIENCE UNIVERSITY OF AUCKLAND AUCKLAND, NEW ZEALANDE-mail: [email protected]
PAVEL SEMUKHIN
Affiliation:
KURT GÖDEL RESEARCH CENTER FOR MATHEMATICAL LOGIC UNIVERSITY OF VIENNA VIENNA, AUSTRIAE-mail: [email protected]
DANIEL TURETSKY
Affiliation:
KURT GÖDEL RESEARCH CENTER FOR MATHEMATICAL LOGIC UNIVERSITY OF VIENNA VIENNA, AUSTRIAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

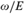Let E be a computably enumerable (c.e.) equivalence relation on the set ω of natural numbers. We say that the quotient set $\omega /E$ (or equivalently, the relation E) realizes a linearly ordered set 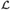${\cal L}$ if there exists a c.e. relation ⊴ respecting E such that the induced structure (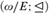$\omega /E$; ⊴) is isomorphic to 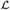${\cal L}$. Thus, one can consider the class of all linearly ordered sets that are realized by 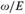$\omega /E$; formally, 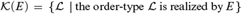${\cal K}\left( E \right) = \left\{ {{\cal L}\,|\,{\rm{the}}\,{\rm{order}}\, - \,{\rm{type}}\,{\cal L}\,{\rm{is}}\,{\rm{realized}}\,{\rm{by}}\,E} \right\}$. In this paper we study the relationship between computability-theoretic properties of E and algebraic properties of linearly ordered sets realized by E. One can also define the following pre-order 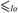$ \le _{lo} $ on the class of all c.e. equivalence relations: 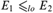$E_1 \le _{lo} E_2 $ if every linear order realized by E1 is also realized by E2. Following the tradition of computability theory, the lo-degrees are the classes of equivalence relations induced by the pre-order 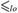$ \le _{lo} $. We study the partially ordered set of lo-degrees. For instance, we construct various chains and anti-chains and show the existence of a maximal element among the lo-degrees.

Keywords

linear ordersequivalence relationscomputability
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 2 , June 2016 , pp. 463 - 482
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Coskey, S., Hamkins, J. D., and Miller, R., The hierarchy of equivalence relations on the natural numbers under computable reducibility . Computability, vol. 1 (2012), no. 1, pp. 15–38.Google Scholar
Feiner, L., Orderings and Boolean algebras not isomorphic to recursive ones , PhD thesis, MIT, 1967.Google Scholar
Fokina, E. and Friedman, S. D., On ${\rm{\Sigma }}_1^1 $ equivalence relations over the natural numbers . Mathematical Logic Quarterly, vol. 58 (2012), no. 1–2, pp. 113–124.Google Scholar
Gao, S. and Gerdes, P., Computably enumerable equivalence relations . Studia Logica, vol. 67 (2001), pp. 27–59.Google Scholar
Gavruskin, A., Khoussainov, B., and Stephan, F., Reducibilities among equivalence relations induced by recursively enumerable structures , CDMTCS Research Report Series, CDMTCS-449, 2014.Google Scholar
Gavryushkin, A., Jain, S., Khoussainov, B., and Stephan, F.. Graphs realized by r.e. equivalence relations . Annals of Pure and Applied Logic, vol. 165 (2014), no. 7–8, pp. 1263–1290.Google Scholar
Jockusch, C., Semirecursive sets and positive reducibility . Transactions of the American Mathematical Society, vol. 131 (1968), pp. 420–436.Google Scholar
Lerman, M., On recursive linear orderings , Logic Year 1979-80, Lecture Notes in Mathematics, pp. 132–142, 1981.Google Scholar