Article contents
Limit ultraproducts
Published online by Cambridge University Press: 12 March 2014
Extract
This paper is a sequel to our earlier paper, “Limit Ultrapowers”, [6]. In that paper we introduced the limit ultrapower construction and proved that 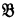 is isomorphic to a limit ultrapower of
is isomorphic to a limit ultrapower of 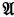 if and only if every PCΔ class which contains
if and only if every PCΔ class which contains 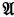 also contains
also contains 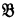 . In Section 1 of this paper we introduce the more general limit ultraproduct construction, and in Section 2 we prove that, for any class K of relational systems, a relational system
. In Section 1 of this paper we introduce the more general limit ultraproduct construction, and in Section 2 we prove that, for any class K of relational systems, a relational system 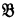 is isomorphic to a limit ultraproduct of members of K if and only if every PCΔ class which includes K also contains
is isomorphic to a limit ultraproduct of members of K if and only if every PCΔ class which includes K also contains 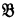 . As a consequence, the property of K being an intersection of PCΔ classes is characterized purely set-theoretically by the property of K being closed under isomorphisms and limit ultraproducts.
. As a consequence, the property of K being an intersection of PCΔ classes is characterized purely set-theoretically by the property of K being closed under isomorphisms and limit ultraproducts.
In Section 3 we apply limit ultraproducts to obtain model-theoretic conditions equivalent to the set-theoretic condition that every α-complete ultrafilter is γ+-complete. The first result, Theorem 3.7, was announced in the abstract [8], and it is also closely related to a result which was stated without proof in [10], namely Theorem 2 of that paper.
In Sections 4 and 5 we apply our results in order to improve a theorem of Craig in [2]. Craig considered the logic L(Q), where Q is a set of cardinals, obtained from ordinary first order logic by adding for each α ϵ Q the quantifier “there exist at least α”.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1965
References
REFERENCES
- 14
- Cited by


