Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T15:44:32.245Z Has data issue: false hasContentIssue false
  • English
  • Français

Les automorphismes d'un ensemble fortement minimal

Published online by Cambridge University Press:  12 March 2014

Daniel Lascar
Daniel Lascar*
Affiliation:
Équipe de Logique Mathématique, Université Paris-VIIet CNRS, 75251 Paris, France, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 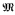be a countable saturated structure, and assume that D(v) is a strongly minimal formula (without parameter) such that 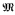is the algebraic closure of D(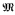). We will prove the two following theorems:

Theorem 1. If G is a subgroup of Aut(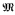) of countable index, there exists a finite set A in 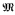such that every A-strong automorphism is in G.

Theorem 2. Assume that G is a normal subgroup of Aut(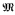) containing an element g such that for all n there exists X ⊆ D(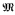) such that Dim(g(X)/X) > n. Then every strong automorphism is in G.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 1 , March 1992 , pp. 238 - 251
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[DNT]Dixon, J. D., Neumann, P. M., and Thomas, S., Subgroups of small index in infinite symmetric groups, Bulletin of the London Mathematical Society, vol. 18 (1986), pp. 580–586.CrossRefGoogle Scholar
[E]Evans, David, Subgroups of small index in general linear groups, Bulletin of the London Mathematical Society, vol. 18 (1986), pp. 587–590.CrossRefGoogle Scholar
[H]Hodges, Wilfrid, Categoricity and permutation groups, Logic Colloquium '87 (Ebbinghaus, H.-D.et al., editors), North-Holland, Amsterdam, 1989, pp. 53–72.Google Scholar
[K]Kuratowski, Kazimierz, Topology, Vol. 1, 5th ed., Academic Press, New York, 1966.Google Scholar
[L1]Lascar, Daniel, Autour de la propriété du petit indice, Proceedings of the London Mathematical Society, ser. 3, vol. 62 (1991), pp. 25–53.CrossRefGoogle Scholar
[L2]Lascar, Daniel, Les beaux automorphismes, Archiv der Mathematik (a paraitre).Google Scholar
[P]Poizat, Bruno, Cours de théorie des modéles, Nur al-Mantiq wal-Ma'rifah, Villeurbanne, 1985.Google Scholar
[Se]Semmes, S. W., Endomorphisms of infinite symmetric groups, Abstracts of Papers Presented to the American Mathematical Society, vol. 2 (1981), p. 426.Google Scholar
[Sh]Shelah, Saharon, Classification theory and the number of non-isomorphic models, North-Holland, Amsterdam, 1978.Google Scholar
[T1]Truss, John K., Infinite permutation groups; subgroups of small index, Journal of Algebra, vol. 120 (1989), pp. 494–515.CrossRefGoogle Scholar
[T2]Truss, John K., Generic automorphisms of homogeneous structures, preprint, University of Leeds, Leeds, 1990.Google Scholar
[ZS]Zariski, O. and Samuel, P., Commutative algebra, Vol. 1, Van Nostrand, Princeton, New Jersey, 1958.Google Scholar