Article contents
Lattice embeddings into the recursively enumerable degrees. II
Published online by Cambridge University Press: 12 March 2014
Extract
The problem of characterizing the finite lattices which can be embedded into the recursively enumerable degrees has a long history, which is summarized in [AL]. This problem is an important one, as its solution is necessary if a decision procedure for the ∀∃-theory of the poset 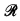 of recursively emumerable degrees is to be found. A recursive nonembeddability condition, NEC, which subsumes all known nonembeddability conditions was presented in [AL]. This paper focuses on embeddability. An embeddability condition, EC, is introduced, and we prove that every finite lattice having EC can be embedded (as a lattice) into
of recursively emumerable degrees is to be found. A recursive nonembeddability condition, NEC, which subsumes all known nonembeddability conditions was presented in [AL]. This paper focuses on embeddability. An embeddability condition, EC, is introduced, and we prove that every finite lattice having EC can be embedded (as a lattice) into 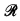 . EC subsumes all known embeddability conditions.
. EC subsumes all known embeddability conditions.
EC is a Π3 condition which states that certain obstructions to proving embeddability do not exist. It seems likely that the recursive labeled trees used in EC can be replaced with trees which are effectively generated from uniformly defined finite trees, in which case EC would be equivalent to a recursive condition. We do not know whether EC and NEC are complementary. This problem seems to be combinatorial, rather than recursion-theoretic in nature. Our efforts to find a finite lattice satisfying neither EC nor NEC have, to this point, been unsuccessful. It is the second author's conjecture that the techniques for proving embeddability which are used in this paper cannot be refined very much to obtain new embeddability results.
EC is introduced in §2, and the various conditions and definitions are motivated by presenting examples of embeddable lattices and indicating how the embedding proof works in those particular cases. The embedding construction is presented in §3, and the proof in §4.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1989
References
REFERENCES
- 17
- Cited by


