Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T18:35:02.992Z Has data issue: false hasContentIssue false
  • English
  • Français

Large families of incomparable A-isols

Published online by Cambridge University Press:  12 March 2014

William S. Heck
William S. Heck*
Affiliation:
Bell Telephone Laboratories, Incorporated, Holmdel New Jersey 07733
Get access Rights & Permissions [Opens in a new window]

Extract

The set Λ of isols was extensively studied by Dekker and Myhill in [1]. Subsequently, Nerode [3] developed the theory of Λ(A), the set of isols relative to some recursively closed set of functions A.

One of the main areas of interest of [1] was the natural partial order ≤ on Λ. In this paper we will examine some of the properties of ≤A on Λ(A). We use the following notations: ∣A∣ is the cardinality of the set A, ⊃ denotes strict inclusion, 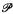(a) is the power set of the set a, c is the cardinality of the continuum, and ω = {0, 1, 2, …}. The terms A-isol, A-immune, A-r.e., A-incomparable, etc. all refer to the usual meaning of these words, only taken in the context of the recursively closed set A. ReqA(a) is the A-r.e.t. of which a is a representative. By identifying a finite natural number with the A-r.e.t. consisting of sets of a given finite cardinality we see that ω ⊆ Λ(A); Λ(A) is said to be nontrivial iff ω ⊃ Λ(A). The three results proven in this paper are:

  1. Theorem 1. If Λ(A) is nontrivial, then ∣Λ(A)∣ = c.

  2. Theorem 2. If∣A∣ < c, then Λ(A) is nontrivial.

  3. Theorem 3. If ∣A∣ < c and ∣⊿∣ < c and ⊿ ⊆ Λ(A) − ω, then there is aΓ ⊆ Λ(A) − ω such that:

  • (a) ∣Γ∣ = c.

  • (b) Every member of Γ is A-incomparable with every member of Δ.

  • (c) Any two distinct members of Γ are A-incomparable.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 48 , Issue 2 , June 1983 , pp. 250 - 252
Copyright
Copyright © Association for Symbolic Logic 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Dekker, J. C. E. and Myhill, J., Recursive equivalence types, University of California Publications in Mathematics, New Series (3), Berkeley, California, 1960, pp. 67–214.Google Scholar
[2]Heck, W., An independent principle of set theory and applications to isols, Ph.D. Thesis, Rutgers University, New Brunswick, New Jersey, 1977.Google Scholar
[3]Nerode, A., Arithmetically isolated sets and non-standard models, Proceedings of Symposia in Pure Mathematics, Vol. V, American Mathematical Society, Providence, Rhode Island, 1962.Google Scholar