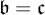1 Introduction
Ideals on countable setsFootnote 1 play a fundamental role in infinite combinatorics. It is for this reason that there is desire to have ways to classify and study them. In [Reference Katětov49] Katětov introduced the following (pre)order:
Definition 1. Let
![]() $X$
and Y be two countable sets,
$X$
and Y be two countable sets,
![]() $\ \mathcal {I},\mathcal {J}$
ideals on X and Y, respectively, and
$\ \mathcal {I},\mathcal {J}$
ideals on X and Y, respectively, and
![]() $f:Y\longrightarrow X$
.
$f:Y\longrightarrow X$
.
-
1. f is a Katětov function from
 $\left ( Y,\mathcal {J}\right ) $
to
$\left ( Y,\mathcal {J}\right ) $
to
 $\left ( X,\mathcal {I}\right ) $
if
$\left ( X,\mathcal {I}\right ) $
if
 $f^{-1}\left ( A\right ) \in \mathcal {J}$
for every
$f^{-1}\left ( A\right ) \in \mathcal {J}$
for every
 $A\in \mathcal {I}.$
$A\in \mathcal {I}.$
-
2.
 $\mathcal {I}\leq _{\textsf {K}}\mathcal {J}$
(
$\mathcal {I}\leq _{\textsf {K}}\mathcal {J}$
(
 $\mathcal {I}$
is Katětov smaller that
$\mathcal {I}$
is Katětov smaller that
 $\mathcal {J}$
or
$\mathcal {J}$
or
 $\mathcal {J}$
is Katětov above
$\mathcal {J}$
is Katětov above
 $\mathcal {I}$
) if there is a Katětov function from
$\mathcal {I}$
) if there is a Katětov function from
 $\left ( Y,\mathcal {J} \right ) $
to
$\left ( Y,\mathcal {J} \right ) $
to
 $\left ( X,\mathcal {I}\right ) .$
$\left ( X,\mathcal {I}\right ) .$
-
3.
 $\mathcal {I}=_{\textsf {K}}\mathcal {J}$
(
$\mathcal {I}=_{\textsf {K}}\mathcal {J}$
(
 $\mathcal {I}$
is Katětov equivalent to
$\mathcal {I}$
is Katětov equivalent to
 $\mathcal {J}$
) if
$\mathcal {J}$
) if
 $\mathcal {I\leq _{\textsf {K} }J}$
and
$\mathcal {I\leq _{\textsf {K} }J}$
and
 $\mathcal {J\leq _{\textsf {K}}I}.$
$\mathcal {J\leq _{\textsf {K}}I}.$
The Katětov order is a powerful tool for studying ideals over countable sets. We will briefly mention two reasons why this is the case (for more information and motivation, the reader may consult [Reference Hrušák37, Reference Hrušák39]). With the Katětov order, it is possible to classify non-definable objects (like MAD families and ultrafilters) using Borel ideals. Almost all of the most interesting properties of ultrafilters can be reformulated in terms of the Katětov order. For example, an ultrafilter
![]() $\mathcal {U}$
is a Ramsey ultrafilter if and only if its dual
$\mathcal {U}$
is a Ramsey ultrafilter if and only if its dual
![]() $\mathcal {U}^{\ast }$
is not Katětov above the ideal
$\mathcal {U}^{\ast }$
is not Katětov above the ideal
![]() $\mathcal {ED}, \mathcal {U}$
is a P-point if and only if
$\mathcal {ED}, \mathcal {U}$
is a P-point if and only if
![]() $\mathcal {U}^{\ast }$
is not Katětov above fin
$\mathcal {U}^{\ast }$
is not Katětov above fin
![]() $\times $
fin and
$\times $
fin and
![]() $\mathcal {U}$
is a nowhere dense ultrafilter if and only if
$\mathcal {U}$
is a nowhere dense ultrafilter if and only if
![]() $\mathcal {U}$
is not Katětov above the ideal nwd (for more information, see [Reference Brendle and Flašková6, Reference Hrušák39]).
$\mathcal {U}$
is not Katětov above the ideal nwd (for more information, see [Reference Brendle and Flašková6, Reference Hrušák39]).
Let X be a set,
![]() $\mathcal {I}$
an ideal on X and
$\mathcal {I}$
an ideal on X and
![]() $\mathbb {P}$
a partial order. We say that
$\mathbb {P}$
a partial order. We say that
![]() $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
![]() $\mathcal {I}$
if
$\mathcal {I}$
if
![]() $\mathbb {P}$
adds a an infinite subset of X that is almost disjoint with every element of
$\mathbb {P}$
adds a an infinite subset of X that is almost disjoint with every element of
![]() $\mathcal {I}.$
This notion is interesting since the theory of destructibility of ideals is very important in forcing. Mainly, many important forcing properties can be stated in these terms. For example, a partial order
$\mathcal {I}.$
This notion is interesting since the theory of destructibility of ideals is very important in forcing. Mainly, many important forcing properties can be stated in these terms. For example, a partial order
![]() $\mathbb {P}$
adds dominating reals if and only if
$\mathbb {P}$
adds dominating reals if and only if
![]() $\mathbb {P}$
destroys fin
$\mathbb {P}$
destroys fin
![]() $\times $
fin or
$\times $
fin or
![]() $\mathbb {P}$
adds eventually different reals if and only if
$\mathbb {P}$
adds eventually different reals if and only if
![]() $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
![]() $\mathcal {ED}.$
It is not hard to prove that if
$\mathcal {ED}.$
It is not hard to prove that if
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
are two ideals such that
$\mathcal {J}$
are two ideals such that
![]() $\mathcal {I\leq _{\textsf {K}}J}$
and
$\mathcal {I\leq _{\textsf {K}}J}$
and
![]() $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
![]() $\mathcal {J},$
then
$\mathcal {J},$
then
![]() $\mathbb {P}$
will also destroy
$\mathbb {P}$
will also destroy
![]() $\mathcal {I}$
(see [Reference Hrušák and Ferreira40]). In this way, the Katětov order helps us understand which ideals are destroyed after performing a forcing extension. Furthermore, the ideals destroyed by Cohen forcing are precisely those ideals that are Katětov below the ideal of the nowhere dense subsets of the rational numbers (there are also similar results for Random, Sacks, Laver, and Miller forcings (see [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44] for more information and related results)).
$\mathcal {I}$
(see [Reference Hrušák and Ferreira40]). In this way, the Katětov order helps us understand which ideals are destroyed after performing a forcing extension. Furthermore, the ideals destroyed by Cohen forcing are precisely those ideals that are Katětov below the ideal of the nowhere dense subsets of the rational numbers (there are also similar results for Random, Sacks, Laver, and Miller forcings (see [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44] for more information and related results)).
The Katětov order is related to the Rudin–Keisler order, which we recall now:
Definition 2. Let
![]() $X$
and Y be two countable sets,
$X$
and Y be two countable sets,
![]() $\ \mathcal {I},\mathcal {J}$
ideals on X and Y, respectively, and
$\ \mathcal {I},\mathcal {J}$
ideals on X and Y, respectively, and
![]() $f:Y\longrightarrow X$
.
$f:Y\longrightarrow X$
.
-
1. f is a Rudin–Keisler function from
 $\left ( Y,\mathcal {J} \right ) $
to
$\left ( Y,\mathcal {J} \right ) $
to
 $\left ( X,\mathcal {I}\right ) $
if for every
$\left ( X,\mathcal {I}\right ) $
if for every
 $A\subseteq X,$
we have that
$A\subseteq X,$
we have that
 $f^{-1}\left ( A\right ) \in \mathcal {J}$
if and only if
$f^{-1}\left ( A\right ) \in \mathcal {J}$
if and only if
 $A\in \mathcal {I}.$
$A\in \mathcal {I}.$
-
2.
 $\mathcal {I\leq _{\textsf {RK}}J}$
(
$\mathcal {I\leq _{\textsf {RK}}J}$
(
 $\mathcal {I}$
is Rudin–Keisler smaller that
$\mathcal {I}$
is Rudin–Keisler smaller that
 $\mathcal {J}$
) if there is a Rudin–Keisler function from
$\mathcal {J}$
) if there is a Rudin–Keisler function from
 $\left ( Y,\mathcal {J}\right ) $
to
$\left ( Y,\mathcal {J}\right ) $
to
 $\left ( X,\mathcal {I}\right ) .$
$\left ( X,\mathcal {I}\right ) .$
It is not hard to see that if
![]() $\mathcal {U}$
and
$\mathcal {U}$
and
![]() $\mathcal {V}$
are ultrafilters, then
$\mathcal {V}$
are ultrafilters, then
![]() $\mathcal {U}^{\ast } \leq _{\textsf {K}} \mathcal {V}^{\ast }$
if and only if
$\mathcal {U}^{\ast } \leq _{\textsf {K}} \mathcal {V}^{\ast }$
if and only if
![]() $\mathcal {U}^{\ast } \leq _{\textsf {RK}}\mathcal {V}^{\ast }.$
The Rudin–Keisler order on ultrafilters (or equivalently, on its duals) has been extensively studied in the past (see [Reference Goldbring27, Reference Halbeisen34, Reference Jech46]). It is interesting that the theory of MAD families under the Katětov order, mirrors the one of ultrafilters. The ideals generated by MAD families are coinitial in the Katětov order, while the duals of ultrafilters are cofinal. Let
$\mathcal {U}^{\ast } \leq _{\textsf {RK}}\mathcal {V}^{\ast }.$
The Rudin–Keisler order on ultrafilters (or equivalently, on its duals) has been extensively studied in the past (see [Reference Goldbring27, Reference Halbeisen34, Reference Jech46]). It is interesting that the theory of MAD families under the Katětov order, mirrors the one of ultrafilters. The ideals generated by MAD families are coinitial in the Katětov order, while the duals of ultrafilters are cofinal. Let
![]() $\mathcal {U}$
be an ultrafilter. In an informal sense, the lower
$\mathcal {U}$
be an ultrafilter. In an informal sense, the lower
![]() $\mathcal {U}^{\ast }$
is in the Katětov order, the more interesting
$\mathcal {U}^{\ast }$
is in the Katětov order, the more interesting
![]() $\mathcal {U}$
is. Dually, the higher a MAD family is in the Katětov order, the more interesting it is. We expect that the theory of MAD families under the Katětov order will be as rich and interesting as the one of ultrafilters.
$\mathcal {U}$
is. Dually, the higher a MAD family is in the Katětov order, the more interesting it is. We expect that the theory of MAD families under the Katětov order will be as rich and interesting as the one of ultrafilters.
The following result is well known (for a proof, the reader may consult [Reference Goldbring27, Reference Halbeisen34, Reference Jech46]).
Proposition 3. Let
![]() $\mathcal {U}$
be an ultrafilter. The following are equivalent
$\mathcal {U}$
be an ultrafilter. The following are equivalent
![]() $:$
$:$
-
1.
 $\mathcal {U}$
is Ramsey.
$\mathcal {U}$
is Ramsey. -
2. If
 $\mathcal {W}$
is an ultrafilter such that
$\mathcal {W}$
is an ultrafilter such that
 $\mathcal {W} ^{\ast } \leq _{\textsf {K}}\mathcal {U}^{\ast },$
then
$\mathcal {W} ^{\ast } \leq _{\textsf {K}}\mathcal {U}^{\ast },$
then
 $\mathcal {U}^{\ast } \leq _{\textsf {K}}\mathcal {W}^{\ast }$
(so
$\mathcal {U}^{\ast } \leq _{\textsf {K}}\mathcal {W}^{\ast }$
(so
 $\mathcal {U}^{\ast }$
and
$\mathcal {U}^{\ast }$
and
 $\mathcal {W}^{\ast }$
are Katětov equivalent).
$\mathcal {W}^{\ast }$
are Katětov equivalent).
In other words, Ramsey ultrafilters are the ultrafilters whose dual is Katětov minimal. Ramsey ultrafilters are very important in Set Theory. It might be interesting to look at the analogue for MAD families.Footnote
2
Given a MAD family
![]() $\mathcal {A},$
by
$\mathcal {A},$
by
![]() $\mathcal {I(A)}$
we denote the ideal generated by
$\mathcal {I(A)}$
we denote the ideal generated by
![]() $\mathcal {A}$
(and finite sets).
$\mathcal {A}$
(and finite sets).
Definition 4. Let
![]() $\mathcal {A}$
be a MAD family. We say that
$\mathcal {A}$
be a MAD family. We say that
![]() $\mathcal {A}$
is Katětov maximal if for every MAD family
$\mathcal {A}$
is Katětov maximal if for every MAD family
![]() $\mathcal {B},$
if
$\mathcal {B},$
if
![]() $\mathcal {I(A)} \leq _{\textsf {K}}\mathcal {I}\left ( \mathcal {B} \right ) ,$
then
$\mathcal {I(A)} \leq _{\textsf {K}}\mathcal {I}\left ( \mathcal {B} \right ) ,$
then
![]() $\mathcal {I(A)} =_{\textsf {K}}\mathcal {I}\left ( \mathcal {B}\right ) $
.
$\mathcal {I(A)} =_{\textsf {K}}\mathcal {I}\left ( \mathcal {B}\right ) $
.
This notion was first consider by García-Ferreira and Hrušák in [Reference Hrušák and Ferreira40]. However, it remained an open problem if such families could exist. This problem was finally answered in [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1] by Arciga, Hrušák, and Martínez:
Theorem 5 (Arciga, Hrušák, and Martínez [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1]).
![]() $\mathfrak {t=c}$
implies that there is a Katětov maximal MAD family.
$\mathfrak {t=c}$
implies that there is a Katětov maximal MAD family.
We will improve the theorem above. In Section 5, we will prove that
![]() $\mathfrak {b=c}$
is enough to build a Katětov maximal MAD family. In Section 6, we will construct Katětov maximal MAD families with additional properties and answer a question of Arciga, Hrušák, and Martínez. It is currently unknown if ZFC proves that there is a Katětov maximal MAD family. In Section 7, we study the Cohen model. We will prove that there is no Katětov maximal MAD family of size
$\mathfrak {b=c}$
is enough to build a Katětov maximal MAD family. In Section 6, we will construct Katětov maximal MAD families with additional properties and answer a question of Arciga, Hrušák, and Martínez. It is currently unknown if ZFC proves that there is a Katětov maximal MAD family. In Section 7, we study the Cohen model. We will prove that there is no Katětov maximal MAD family of size
![]() $\omega _{1}$
in the Cohen model. It is worth pointing out that MAD families of size
$\omega _{1}$
in the Cohen model. It is worth pointing out that MAD families of size
![]() $\omega _{1}$
do exist in the model (see [Reference Kunen50]).
$\omega _{1}$
do exist in the model (see [Reference Kunen50]).
We now turn our attention to an even stronger property than maximality. This property was also studied by García-Ferreira and Hrušák in [Reference Hrušák and Ferreira40].
Definition 6. Let
![]() $\mathcal {A}$
be a MAD family. We say that
$\mathcal {A}$
be a MAD family. We say that
![]() $\mathcal {A}$
is Katětov-top if
$\mathcal {A}$
is Katětov-top if
![]() $\mathcal {I(B)} \leq _{\textsf {K}} \mathcal {I}(\mathcal {A})$
for every MAD family
$\mathcal {I(B)} \leq _{\textsf {K}} \mathcal {I}(\mathcal {A})$
for every MAD family
![]() $\mathcal {B}.$
$\mathcal {B}.$
Contrary to Katětov maximal MAD families, one would expect that Katětov-top MAD families do not exist. In [Reference Hrušák and Ferreira40] the following partial result was obtained:
Theorem 7 (García-Ferreira and Hrušák [Reference Hrušák and Ferreira40]).
![]() $\mathfrak {b=c}$
implies that there are no Katětov-top MAD families.
$\mathfrak {b=c}$
implies that there are no Katětov-top MAD families.
We will improve this theorem and show that there are no such families under
![]() $\mathfrak {s\leq b}$
. It is still unknown if ZFC proves that Katětov-top MAD families do not exist. We include some discussion of this in Section 4.
$\mathfrak {s\leq b}$
. It is still unknown if ZFC proves that Katětov-top MAD families do not exist. We include some discussion of this in Section 4.
2 Notation
A family
![]() $\mathcal {A}\subseteq \left [ \omega \right ] ^{\omega }$
is almost disjoint (AD) if the intersection of any two different elements of
$\mathcal {A}\subseteq \left [ \omega \right ] ^{\omega }$
is almost disjoint (AD) if the intersection of any two different elements of
![]() $\mathcal {A}$
is finite, a MAD family is a maximal almost disjoint family. To avoid trivial considerations, we always assume MAD families to be infinite.
$\mathcal {A}$
is finite, a MAD family is a maximal almost disjoint family. To avoid trivial considerations, we always assume MAD families to be infinite.
Given a set
![]() $X,$
by
$X,$
by
![]() $\mathcal {P}\left ( X\right ) $
we denote the power set of
$\mathcal {P}\left ( X\right ) $
we denote the power set of
![]() $X.$
Let f be a function. By dom
$X.$
Let f be a function. By dom
![]() $\left ( f\right ) $
we denote the domain of X and by img
$\left ( f\right ) $
we denote the domain of X and by img
![]() $\left ( f\right ) $
we denote its image. We say f is a partial function from X to Y (where X and Y are two sets) if dom
$\left ( f\right ) $
we denote its image. We say f is a partial function from X to Y (where X and Y are two sets) if dom
![]() $\left ( f\right ) \subseteq X$
and img
$\left ( f\right ) \subseteq X$
and img
![]() $\left ( f\right ) \subseteq Y.$
This will be denoted by f
$\left ( f\right ) \subseteq Y.$
This will be denoted by f
![]() $;X\longrightarrow Y.$
Given
$;X\longrightarrow Y.$
Given
![]() $A\subseteq X,$
by
$A\subseteq X,$
by
![]() $f\left [ A\right ] $
we denote
$f\left [ A\right ] $
we denote
![]() $f\left [ A\cap {\textsf {dom}}\left ( f\right ) \right ] .$
$f\left [ A\cap {\textsf {dom}}\left ( f\right ) \right ] .$
Definition 8. Let X be a set.
-
1. We say that
 $\mathcal {F\subseteq } \wp \left ( X\right ) $
is a filter on X if the following conditions hold
$\mathcal {F\subseteq } \wp \left ( X\right ) $
is a filter on X if the following conditions hold
 $:$
$:$
-
(a)
 $X\in \mathcal {F}$
and
$X\in \mathcal {F}$
and
 $\emptyset \notin \mathcal {F}.$
$\emptyset \notin \mathcal {F}.$
-
(b) If
 $A\in \mathcal {F}$
and
$A\in \mathcal {F}$
and
 $A\subseteq B$
then
$A\subseteq B$
then
 $B\in \mathcal {F}.$
$B\in \mathcal {F}.$
-
(c) If
 $A,B\in \mathcal {F}$
then
$A,B\in \mathcal {F}$
then
 $A\cap B\in \mathcal {F}.$
$A\cap B\in \mathcal {F}.$
-
-
2. We say that
 $\mathcal {I\subseteq } \wp \left ( X\right ) $
is an ideal on X if the following conditions hold
$\mathcal {I\subseteq } \wp \left ( X\right ) $
is an ideal on X if the following conditions hold
 $:$
$:$
-
(a) Every finite subset of X is in
 $\mathcal {I}.$
$\mathcal {I}.$
-
(b) If
 $A\in \mathcal {I}$
and
$A\in \mathcal {I}$
and
 $B\subseteq A$
then
$B\subseteq A$
then
 $B\in \mathcal {I}.$
$B\in \mathcal {I}.$
-
(c) If
 $A,B\in \mathcal {I}$
then
$A,B\in \mathcal {I}$
then
 $A\cup B\in \mathcal {I}.$
$A\cup B\in \mathcal {I}.$
-
We will be mainly interested in filters and ideals on countable sets. An ideal
![]() $\mathcal {I\subseteq } \wp \left ( X\right ) $
is a proper ideal if
$\mathcal {I\subseteq } \wp \left ( X\right ) $
is a proper ideal if
![]() $X\notin \mathcal {I},$
otherwise it is called an improper ideal. We say that
$X\notin \mathcal {I},$
otherwise it is called an improper ideal. We say that
![]() $\mathcal {I}$
is tall if for every infinite
$\mathcal {I}$
is tall if for every infinite
![]() $A\subseteq X,$
there is
$A\subseteq X,$
there is
![]() $I\in \mathcal {I}$
such that
$I\in \mathcal {I}$
such that
![]() $A\cap I$
is infinite. By fin we denote the ideal of finite subsets of
$A\cap I$
is infinite. By fin we denote the ideal of finite subsets of
![]() $\omega .$
$\omega .$
Definition 9. Let
![]() $\mathcal {A}$
be an AD family on
$\mathcal {A}$
be an AD family on
![]() $\omega .$
$\omega .$
-
1.
 $\mathcal {I}\left ( \mathcal {A}\right ) $
is the ideal generated by
$\mathcal {I}\left ( \mathcal {A}\right ) $
is the ideal generated by
 $\mathcal {A}.$
In other words,
$\mathcal {A}.$
In other words,
 $X\in \mathcal {I}\left ( \mathcal {A}\right ) $
if and only if there are
$X\in \mathcal {I}\left ( \mathcal {A}\right ) $
if and only if there are
 $A_{0},\dots ,A_{n}\in \mathcal {A}$
and s a finite set such that
$A_{0},\dots ,A_{n}\in \mathcal {A}$
and s a finite set such that
 $X\subseteq A_{0}\cup \dots \cup A_{n}\cup s.$
$X\subseteq A_{0}\cup \dots \cup A_{n}\cup s.$
-
2.
 $\mathcal {I}\left ( \mathcal {A}\right ) ^{+}$
is the collection of all subsets of
$\mathcal {I}\left ( \mathcal {A}\right ) ^{+}$
is the collection of all subsets of
 $\omega $
that are not in
$\omega $
that are not in
 $\mathcal {I}\left ( \mathcal {A}\right ) .$
$\mathcal {I}\left ( \mathcal {A}\right ) .$
-
3.
 $\mathcal {I}\left ( \mathcal {A}\right ) ^{++}$
is the set of all
$\mathcal {I}\left ( \mathcal {A}\right ) ^{++}$
is the set of all
 $X\subseteq \omega $
for which there is
$X\subseteq \omega $
for which there is
 $\mathcal {B\in } \left [ \mathcal {A} \right ] ^{\omega }$
such that if
$\mathcal {B\in } \left [ \mathcal {A} \right ] ^{\omega }$
such that if
 $A\in \mathcal {B}$
then
$A\in \mathcal {B}$
then
 $X\cap A$
is infinite.
$X\cap A$
is infinite. -
4.
 $\mathcal {A}^{\perp }$
is the set of all
$\mathcal {A}^{\perp }$
is the set of all
 $X\subseteq \omega $
such that
$X\subseteq \omega $
such that
 $\left \vert X\cap A\right \vert <\omega $
for every
$\left \vert X\cap A\right \vert <\omega $
for every
 $A\in \mathcal {A}.$
$A\in \mathcal {A}.$
-
5. Let
 $X\in \left [ \omega \right ] ^{\omega }.$
Define
$X\in \left [ \omega \right ] ^{\omega }.$
Define
 $\mathcal {A} \upharpoonright X=\left \{ A\cap X\mid A\in \mathcal {A}\right \} \setminus \left [ \omega \right ] ^{<\omega }.$
$\mathcal {A} \upharpoonright X=\left \{ A\cap X\mid A\in \mathcal {A}\right \} \setminus \left [ \omega \right ] ^{<\omega }.$
-
6. We say
 $\mathcal {A}$
is nowhere MAD if for every
$\mathcal {A}$
is nowhere MAD if for every
 $X\in \mathcal {I}\left ( \mathcal {A}\right ) ^{+},$
there is
$X\in \mathcal {I}\left ( \mathcal {A}\right ) ^{+},$
there is
 $Y\in \left [ X\right ] ^{\omega }$
such that
$Y\in \left [ X\right ] ^{\omega }$
such that
 $Y\in \mathcal {A}^{\perp }.$
In other words,
$Y\in \mathcal {A}^{\perp }.$
In other words,
 $\mathcal {A} \upharpoonright X$
is not maximal in
$\mathcal {A} \upharpoonright X$
is not maximal in
 $X.$
$X.$
The cardinal invariants of the continuum play a leading role in this paper. We list the cardinal invariants that will be needed. The reader can learn about cardinal invariants in [Reference Blass4]. In almost all instances in the paper, the expression “almost all” means that the set of exceptions is finite.
-
1. The almost disjointness number
 $\mathfrak {a}$
is the smallest size of a MAD family.
$\mathfrak {a}$
is the smallest size of a MAD family. -
2. The size of the continuum is denoted by
 $\mathfrak {c}.$
$\mathfrak {c}.$
-
3. Let
 $f,g\in \omega ^{\omega }.$
By
$f,g\in \omega ^{\omega }.$
By
 $f\leq ^{\ast }g$
we mean that
$f\leq ^{\ast }g$
we mean that
 $f\left ( n\right ) \leq g\left ( n\right ) $
holds for almost all
$f\left ( n\right ) \leq g\left ( n\right ) $
holds for almost all
 $n\in \omega .$
The expression
$n\in \omega .$
The expression
 $f\leq _{n}g$
means that if
$f\leq _{n}g$
means that if
 $m\geq n,$
then
$m\geq n,$
then
 $f\left ( m\right ) \leq g\left ( m\right ) .$
$f\left ( m\right ) \leq g\left ( m\right ) .$
-
4. The bounding number
 $\mathfrak {b}$
is the smallest size of an unbounded family of functions (with respect to the
$\mathfrak {b}$
is the smallest size of an unbounded family of functions (with respect to the
 $\leq ^{\ast }$
ordering).
$\leq ^{\ast }$
ordering). -
5. Let
 $A,B\in \left [ \omega \right ] ^{\omega }.$
The expression
$A,B\in \left [ \omega \right ] ^{\omega }.$
The expression
 $A\subseteq ^{\ast }B$
means that
$A\subseteq ^{\ast }B$
means that
 $A\setminus B$
is finite. In this case, we say that A is almost contained in
$A\setminus B$
is finite. In this case, we say that A is almost contained in
 $B.$
$B.$
-
6. Let
 $\mathcal {H}\subseteq \left [ \omega \right ] ^{\omega }.$
We say that
$\mathcal {H}\subseteq \left [ \omega \right ] ^{\omega }.$
We say that
 $\mathcal {H}$
is centered if for every
$\mathcal {H}$
is centered if for every
 $n\in \omega $
and
$n\in \omega $
and
 $A_{0} ,\dots ,A_{n}\in \mathcal {H},$
it is the case that
$A_{0} ,\dots ,A_{n}\in \mathcal {H},$
it is the case that
 $A_{0}\cap \dots \cap A_{n}$
is infinite. We say that
$A_{0}\cap \dots \cap A_{n}$
is infinite. We say that
 $P\in \left [ \omega \right ] ^{\omega }$
is a pseudointersection of
$P\in \left [ \omega \right ] ^{\omega }$
is a pseudointersection of
 $\mathcal {H}$
if P is almost contained in every member of
$\mathcal {H}$
if P is almost contained in every member of
 $\mathcal {H}.$
$\mathcal {H}.$
-
7. The pseudointersection number
 $\mathfrak {p}$
is the smallest size of a centered family with no infinite pseudointersection.
$\mathfrak {p}$
is the smallest size of a centered family with no infinite pseudointersection. -
8. A family
 $\mathcal {H}=\left \{ A_{\alpha }\mid \alpha <\kappa \right \} \subseteq \left [ \omega \right ] ^{\omega }$
is a tower if
$\mathcal {H}=\left \{ A_{\alpha }\mid \alpha <\kappa \right \} \subseteq \left [ \omega \right ] ^{\omega }$
is a tower if
 $A_{\alpha }\subseteq ^{\ast }A_{\beta }$
whenever
$A_{\alpha }\subseteq ^{\ast }A_{\beta }$
whenever
 $\alpha>\beta $
and
$\alpha>\beta $
and
 $\mathcal {H}$
has no infinite pseudointersections.
$\mathcal {H}$
has no infinite pseudointersections. -
9. The tower number
 $\mathfrak {t}$
is the smallest size of a tower.
$\mathfrak {t}$
is the smallest size of a tower. -
10. Let
 $\mathcal {D} \subseteq \left [ \omega \right ] ^{\omega }.$
We say that
$\mathcal {D} \subseteq \left [ \omega \right ] ^{\omega }.$
We say that
 $\mathcal {D}$
is dense in
$\mathcal {D}$
is dense in
 $\left [ \omega \right ] ^{\omega }$
if for every
$\left [ \omega \right ] ^{\omega }$
if for every
 $A\in \left [ \omega \right ] ^{\omega }$
there is
$A\in \left [ \omega \right ] ^{\omega }$
there is
 $B\in \mathcal {D}$
such that
$B\in \mathcal {D}$
such that
 $B\subseteq ^{\ast }A.$
We say
$B\subseteq ^{\ast }A.$
We say
 $\mathcal {D}$
is open in
$\mathcal {D}$
is open in
 $\left [ \omega \right ] ^{\omega }$
if for every
$\left [ \omega \right ] ^{\omega }$
if for every
 $A\in \mathcal {D},$
if
$A\in \mathcal {D},$
if
 $B\subseteq ^{\ast }A,$
then
$B\subseteq ^{\ast }A,$
then
 $B\in \mathcal {D}.$
We say that
$B\in \mathcal {D}.$
We say that
 $\mathcal {D}$
is open dense in
$\mathcal {D}$
is open dense in
 $\left [ \omega \right ] ^{\omega }$
if it is both open and dense in
$\left [ \omega \right ] ^{\omega }$
if it is both open and dense in
 $\left [ \omega \right ] ^{\omega }.$
$\left [ \omega \right ] ^{\omega }.$
-
11. The distributivity number
 $\mathfrak {h}$
is the smallest size of a family of open dense sets in
$\mathfrak {h}$
is the smallest size of a family of open dense sets in
 $\left [ \omega \right ] ^{\omega }$
with empty intersection.
$\left [ \omega \right ] ^{\omega }$
with empty intersection. -
12. The uniformity of the meager ideal non
 $\left ( \mathcal {M}\right ) $
is the smallest size of a nonmeager subset of the Baire space
$\left ( \mathcal {M}\right ) $
is the smallest size of a nonmeager subset of the Baire space
 $\omega ^{\omega }.$
$\omega ^{\omega }.$
A celebrated theorem of Malliaris and Shelah is that
![]() $\mathfrak {p}$
and
$\mathfrak {p}$
and
![]() $\mathfrak {t}$
are equal (see [Reference Malliaris and Shelah53]). Since we will be referencing theorems in papers that were written before it was proved that these two cardinal invariants are the same, we will be writing
$\mathfrak {t}$
are equal (see [Reference Malliaris and Shelah53]). Since we will be referencing theorems in papers that were written before it was proved that these two cardinal invariants are the same, we will be writing
![]() $\mathfrak {p}$
or
$\mathfrak {p}$
or
![]() $\mathfrak {t}$
depending on how it was written in the cited paper. It is well-known that
$\mathfrak {t}$
depending on how it was written in the cited paper. It is well-known that
![]() $\mathfrak {p\leq h\leq b\leq a\leq c}$
and
$\mathfrak {p\leq h\leq b\leq a\leq c}$
and
![]() $\mathfrak {b\leq }$
non
$\mathfrak {b\leq }$
non
![]() $\left ( \mathcal {M}\right ) \leq \mathfrak {c}$
(the proofs of these inequalities can be consulted in [Reference Blass4]). There is no provable relation between non
$\left ( \mathcal {M}\right ) \leq \mathfrak {c}$
(the proofs of these inequalities can be consulted in [Reference Blass4]). There is no provable relation between non
![]() $\left ( \mathcal {M}\right ) $
and
$\left ( \mathcal {M}\right ) $
and
![]() $\mathfrak {a},$
although it is an open question if non
$\mathfrak {a},$
although it is an open question if non
![]() $\left ( \mathcal {M}\right ) =\omega _{1}$
implies that
$\left ( \mathcal {M}\right ) =\omega _{1}$
implies that
![]() $\mathfrak {a}=\omega _{1}.$
$\mathfrak {a}=\omega _{1}.$
By
![]() $\omega ^{<\omega \nearrow }$
we denote the set of all finite increasing sequences of
$\omega ^{<\omega \nearrow }$
we denote the set of all finite increasing sequences of
![]() $\omega .$
Given
$\omega .$
Given
![]() $A\in \left [ \omega \right ] ^{\omega },$
its enumerating function is the unique increasing bijection between
$A\in \left [ \omega \right ] ^{\omega },$
its enumerating function is the unique increasing bijection between
![]() $\omega $
and
$\omega $
and
![]() $A.$
By identifying each set with its characteristic function, we can view ideals or filters on
$A.$
By identifying each set with its characteristic function, we can view ideals or filters on
![]() $\omega $
as subspaces of the Cantor space
$\omega $
as subspaces of the Cantor space
![]() $2^{\omega }.$
In this way, we can say when an ideal is Borel or analytic. By fin we denote the ideal of finite subsets of
$2^{\omega }.$
In this way, we can say when an ideal is Borel or analytic. By fin we denote the ideal of finite subsets of
![]() $\omega $
and nwddenotes the ideal of nowhere dense subsets of the rational numbers.
$\omega $
and nwddenotes the ideal of nowhere dense subsets of the rational numbers.
3 Preliminaries
In this section, we will recall some properties of the Katětov order and AD families. Nothing in this section is really new, but we will take the opportunity to state explicitly some lemmas that only appear implicitly in the literature. We only provide proofs of the statements that (to the best of our knowledge) have not been explicitly proved elsewhere.
For convenience, if
![]() $\mathcal {A}$
is an AD family and
$\mathcal {A}$
is an AD family and
![]() $\mathcal {J}$
an ideal, we will write
$\mathcal {J}$
an ideal, we will write
![]() $\mathcal {A}\leq _{\textsf {K}}\mathcal {J}$
(
$\mathcal {A}\leq _{\textsf {K}}\mathcal {J}$
(
![]() $\mathcal {J}\leq _{\textsf {K}}\mathcal {A}$
) instead of
$\mathcal {J}\leq _{\textsf {K}}\mathcal {A}$
) instead of
![]() $\mathcal {I(A)} \leq _{\textsf {K}}\mathcal {J}$
(
$\mathcal {I(A)} \leq _{\textsf {K}}\mathcal {J}$
(
![]() $\mathcal {J}\leq _{\textsf {K}} \mathcal {I(A)}$
). We start recalling the most basic remarks about the Katětov order (see [Reference Hrušák and Ferreira40] for a proof):
$\mathcal {J}\leq _{\textsf {K}} \mathcal {I(A)}$
). We start recalling the most basic remarks about the Katětov order (see [Reference Hrušák and Ferreira40] for a proof):
Lemma 10. Let
![]() $\mathcal {I},\mathcal {J},\mathcal {L}$
be ideals and
$\mathcal {I},\mathcal {J},\mathcal {L}$
be ideals and
![]() $\mathcal {A} ,\mathcal {B}$
two AD families.
$\mathcal {A} ,\mathcal {B}$
two AD families.
-
1.
 $\mathcal {I=_{\textsf {K}}I}.$
$\mathcal {I=_{\textsf {K}}I}.$
-
2. If
 $\mathcal {I\leq _{\textsf {K}}J}$
and
$\mathcal {I\leq _{\textsf {K}}J}$
and
 $\mathcal {J\leq _{\textsf {K}}L},$
then
$\mathcal {J\leq _{\textsf {K}}L},$
then
 $\mathcal {I\leq _{\textsf {K}}L}.$
$\mathcal {I\leq _{\textsf {K}}L}.$
-
3. fin is the smallest element in the Katětov order.
-
4.
 $\mathcal {I}$
is Katětov equivalent to fin if and only if
$\mathcal {I}$
is Katětov equivalent to fin if and only if
 $\mathcal {I}$
is not tall.
$\mathcal {I}$
is not tall. -
5.
 $\mathcal {A}$
is MAD if and only if
$\mathcal {A}$
is MAD if and only if
 $\mathcal {A}\nleq _{\textsf {K}}$
fin.
$\mathcal {A}\nleq _{\textsf {K}}$
fin. -
6. If
 $X\in \mathcal {I}\left ( \mathcal {A}\right ) ^{+},$
then
$X\in \mathcal {I}\left ( \mathcal {A}\right ) ^{+},$
then
 $\mathcal {A}\leq _{\textsf {K}} \mathcal {A}\upharpoonright X.$
$\mathcal {A}\leq _{\textsf {K}} \mathcal {A}\upharpoonright X.$
-
7. If
 $\mathcal {A}\leq _{\textsf {K}} \mathcal {B},$
then
$\mathcal {A}\leq _{\textsf {K}} \mathcal {B},$
then
 $\left \vert \mathcal {B}\right \vert \leq \left \vert \mathcal {A}\right \vert .$
$\left \vert \mathcal {B}\right \vert \leq \left \vert \mathcal {A}\right \vert .$
The following is a useful reformulation of the Katětov order:
Lemma 11. Let
![]() $X,Y$
countable sets,
$X,Y$
countable sets,
![]() $\mathcal {I}$
an ideal on
$\mathcal {I}$
an ideal on
![]() $X, \mathcal {J}$
an ideal on Y and
$X, \mathcal {J}$
an ideal on Y and
![]() $f:X\longrightarrow Y.$
The following are equivalent
$f:X\longrightarrow Y.$
The following are equivalent
![]() $:$
$:$
-
1. f is a Katětov function from
 $(X,\mathcal {I})$
to
$(X,\mathcal {I})$
to
 $(Y,\mathcal {J} ).$
$(Y,\mathcal {J} ).$
-
2. If
 $A\in \mathcal {I}^{+},$
then
$A\in \mathcal {I}^{+},$
then
 $f\left [ A\right ] \in \mathcal {J}^{+}.$
$f\left [ A\right ] \in \mathcal {J}^{+}.$
Proof We first prove that the first point implies the second. Assume f is a Katětov function from
![]() $(X,\mathcal {I})$
to
$(X,\mathcal {I})$
to
![]() $(Y,\mathcal {J})$
and let
$(Y,\mathcal {J})$
and let
![]() $A\in \mathcal {I}^{+}.$
We know that
$A\in \mathcal {I}^{+}.$
We know that
![]() $A\subseteq f^{-1}\left ( f\left [ A\right ] \right ) ,$
hence
$A\subseteq f^{-1}\left ( f\left [ A\right ] \right ) ,$
hence
![]() $f^{-1}\left ( f\left [ A\right ] \right ) \in \mathcal {I}^{+}.$
Since f is a Katětov function, we must have that
$f^{-1}\left ( f\left [ A\right ] \right ) \in \mathcal {I}^{+}.$
Since f is a Katětov function, we must have that
![]() $f\left [ A\right ] \in \mathcal {J}^{+}.$
$f\left [ A\right ] \in \mathcal {J}^{+}.$
Now assume that f sends
![]() $\mathcal {I}^{+}$
sets to
$\mathcal {I}^{+}$
sets to
![]() $\mathcal {J}^{+}$
sets, we will prove that f is a Katětov function. Let
$\mathcal {J}^{+}$
sets, we will prove that f is a Katětov function. Let
![]() $B\in \mathcal {J}.$
Since
$B\in \mathcal {J}.$
Since
![]() $f[f^{-1}\left ( B\right ) ]\subseteq B,$
it follows that
$f[f^{-1}\left ( B\right ) ]\subseteq B,$
it follows that
![]() $f[f^{-1}\left ( B\right ) ]\in \mathcal {J}.$
Using the hypothesis we conclude that
$f[f^{-1}\left ( B\right ) ]\in \mathcal {J}.$
Using the hypothesis we conclude that
![]() $f^{-1}\left ( B\right ) \in \mathcal {I}.$
$f^{-1}\left ( B\right ) \in \mathcal {I}.$
We now recall some special properties of MAD families, which will play a crucial role in the paper.
Definition 12. Let
![]() $\mathcal {A}$
be a MAD family.
$\mathcal {A}$
be a MAD family.
-
1.
 $\mathcal {A}$
is tight if for every
$\mathcal {A}$
is tight if for every
 $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \mathcal {I}\left ( \mathcal {A}\right ) ^{+}$
there is
$\left \{ X_{n}\mid n\in \omega \right \} \subseteq \mathcal {I}\left ( \mathcal {A}\right ) ^{+}$
there is
 $B\in \mathcal {I}\left ( \mathcal {A}\right ) $
such that
$B\in \mathcal {I}\left ( \mathcal {A}\right ) $
such that
 $B\cap X_{n}$
is infinite for every
$B\cap X_{n}$
is infinite for every
 $n\in \omega .$
$n\in \omega .$
-
2.
 $\mathcal {A}$
is weakly tight if for every
$\mathcal {A}$
is weakly tight if for every
 $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \mathcal {I}\left ( \mathcal {A}\right ) ^{+}$
there is
$\left \{ X_{n}\mid n\in \omega \right \} \subseteq \mathcal {I}\left ( \mathcal {A}\right ) ^{+}$
there is
 $B\in \mathcal {I}\left ( \mathcal {A}\right ) $
such that
$B\in \mathcal {I}\left ( \mathcal {A}\right ) $
such that
 $\left \vert B\cap X_{n}\right \vert =\omega $
for infinitely many
$\left \vert B\cap X_{n}\right \vert =\omega $
for infinitely many
 $n\in \omega .$
$n\in \omega .$
-
3.
 $\mathcal {A}$
is completely separable if for every
$\mathcal {A}$
is completely separable if for every
 $X\in \mathcal {I(A)}^{+}$
there is
$X\in \mathcal {I(A)}^{+}$
there is
 $A\in \mathcal {A}$
such that
$A\in \mathcal {A}$
such that
 $A\subseteq X.$
$A\subseteq X.$
It is currently unknown if ZFC implies the existence of any of this type of MAD families, but significant progress has been obtained in each case. The existence of a completely separable MAD family is a famous problem of Erdoős and Shelah (see [Reference Erdős and Shelah20], also [Reference Hrušák, Steprans and Zhang43]). It is easy to prove that consistently the answer is affirmative. Most of the early work on this problem was done by Balcar and Simon (see [Reference Balcar and Simon2]). They proved that completely separable MAD families exist assuming one of the following:
![]() $\mathfrak {a=c}$
,
$\mathfrak {a=c}$
,
![]() $\mathfrak {b=d,} \mathfrak {d\leq a}$
, or
$\mathfrak {b=d,} \mathfrak {d\leq a}$
, or
![]() $\mathfrak {s} =\omega _{1}.$
A major advance was done by Shelah himself in [Reference Shelah61] (see also [Reference Guzmán28, Reference Hrušák38, Reference Mildenberger, Raghavan and Steprans56]). He proved that there is a completely separable MAD family if either
$\mathfrak {s} =\omega _{1}.$
A major advance was done by Shelah himself in [Reference Shelah61] (see also [Reference Guzmán28, Reference Hrušák38, Reference Mildenberger, Raghavan and Steprans56]). He proved that there is a completely separable MAD family if either
![]() $\mathfrak {s<a}$
or
$\mathfrak {s<a}$
or
![]() $\mathfrak {s\geq a}$
and a certain “PCF hypothesis” holds. In [Reference Mildenberger, Raghavan and Steprans56] Mildenberger, Raghavan, and Steprāns (building from results in [Reference Raghavan and Steprāns59]) were able to eliminate the extra hypothesis in the case of
$\mathfrak {s\geq a}$
and a certain “PCF hypothesis” holds. In [Reference Mildenberger, Raghavan and Steprans56] Mildenberger, Raghavan, and Steprāns (building from results in [Reference Raghavan and Steprāns59]) were able to eliminate the extra hypothesis in the case of
![]() $\mathfrak {s=a.}$
In this way,
$\mathfrak {s=a.}$
In this way,
![]() $\mathfrak {s\leq a}$
implies that there is a completely separable MAD family. Moreover, building from the work of Shelah, Mildenberger, Raghavan, and Steprāns proved the following theorem:
$\mathfrak {s\leq a}$
implies that there is a completely separable MAD family. Moreover, building from the work of Shelah, Mildenberger, Raghavan, and Steprāns proved the following theorem:
Theorem 13 (Mildenberger, Raghavan, and Steprāns [Reference Mildenberger, Raghavan and Steprans56] and [Reference Raghavan and Steprāns59]).
If
![]() $\mathfrak {s\leq b,}$
then there is a completely separable weakly tight MAD family.
$\mathfrak {s\leq b,}$
then there is a completely separable weakly tight MAD family.
Regarding tight MAD families, Hrušák and Kurilic independently proved the following:
Proposition 14 (Hrušák [Reference Hrušák36], Kurilic [Reference Kurilić51]).
![]() $\mathfrak {b=c}$
implies that there is a completely separable tight MAD family.
$\mathfrak {b=c}$
implies that there is a completely separable tight MAD family.
In [Reference Guzmán and Hrušák32] it is proved that the diamond principle
![]() $\Diamond (\mathfrak {b})$
of [Reference Moore, Hrušák and Džamonja58] also implies that there is a tight MAD family.
$\Diamond (\mathfrak {b})$
of [Reference Moore, Hrušák and Džamonja58] also implies that there is a tight MAD family.
Lemma 15. Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be two MAD families. If
$\mathcal {B}$
be two MAD families. If
![]() $\mathcal {A}$
is (weakly) tight and
$\mathcal {A}$
is (weakly) tight and
![]() $\mathcal {A}\leq _{\textsf {K}} \mathcal {B},$
then
$\mathcal {A}\leq _{\textsf {K}} \mathcal {B},$
then
![]() $\mathcal {B}$
is also (weakly) tight.
$\mathcal {B}$
is also (weakly) tight.
Proof Let
![]() $f\in \omega ^{\omega }$
be a Katětov function from
$f\in \omega ^{\omega }$
be a Katětov function from
![]() $(\omega ,\mathcal {I(B)})$
to
$(\omega ,\mathcal {I(B)})$
to
![]() $(\omega ,\mathcal {I(A)}).$
Let
$(\omega ,\mathcal {I(A)}).$
Let
![]() $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \mathcal {I(B)}^{+}.$
By Lemma 11, we know that
$\left \{ X_{n}\mid n\in \omega \right \} \subseteq \mathcal {I(B)}^{+}.$
By Lemma 11, we know that
![]() $\left \{ f\left [ X_{n}\right ] \mid n\in \omega \right \} \subseteq \mathcal {I(A)}^{+}.$
Since
$\left \{ f\left [ X_{n}\right ] \mid n\in \omega \right \} \subseteq \mathcal {I(A)}^{+}.$
Since
![]() $\mathcal {A}$
is (weakly) tight, we can find
$\mathcal {A}$
is (weakly) tight, we can find
![]() $A\in \mathcal {I(A)}$
such that
$A\in \mathcal {I(A)}$
such that
![]() $A\cap f\left [ X_{n}\right ] $
is infinite for all (for infinitely many)
$A\cap f\left [ X_{n}\right ] $
is infinite for all (for infinitely many)
![]() $n\in \omega .$
It follows that
$n\in \omega .$
It follows that
![]() $f^{-1}\left ( A\right ) \in \mathcal {I(B)}$
and has infinite intersection with all (infinitely many) of the
$f^{-1}\left ( A\right ) \in \mathcal {I(B)}$
and has infinite intersection with all (infinitely many) of the
![]() $X_{n}.$
$X_{n}.$
We now recall the notion of forcing destructibility:
Definition 16. Let
![]() $\mathbb {P}$
be a forcing notion,
$\mathbb {P}$
be a forcing notion,
![]() $\mathcal {I}$
an ideal and
$\mathcal {I}$
an ideal and
![]() $\mathcal {A}$
a MAD family.
$\mathcal {A}$
a MAD family.
-
1.
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $\mathbb {P}$
-destructible if
$\mathbb {P}$
-destructible if
 $\mathcal {I}$
is no longer tall after forcing with
$\mathcal {I}$
is no longer tall after forcing with
 $\mathbb {P}.$
$\mathbb {P}.$
-
2.
 $\mathcal {A}$
is
$\mathcal {A}$
is
 $\mathbb {P}$
-destructible if
$\mathbb {P}$
-destructible if
 $\mathcal {A}$
is no longer maximal after forcing with
$\mathcal {A}$
is no longer maximal after forcing with
 $\mathbb {P}.$
$\mathbb {P}.$
It is easy to see that a MAD family is
![]() $\mathbb {P}$
-destructible if and only if its ideal generated is
$\mathbb {P}$
-destructible if and only if its ideal generated is
![]() $\mathbb {P}$
-destructible. The topic of indestructibility has obtained a lot of attention recently, yet there are still many interesting problems that remain open. To learn more about indestructibility of ideals and MAD families, the reader may consult [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44] and the survey [Reference Chodounský and Guzmán14]. Forcing indestructibility and the Katětov order are related as follows:
$\mathbb {P}$
-destructible. The topic of indestructibility has obtained a lot of attention recently, yet there are still many interesting problems that remain open. To learn more about indestructibility of ideals and MAD families, the reader may consult [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44] and the survey [Reference Chodounský and Guzmán14]. Forcing indestructibility and the Katětov order are related as follows:
Lemma 17 [Reference Hrušák and Ferreira40].
Let
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
be two ideals and
$\mathcal {J}$
be two ideals and
![]() $\mathbb {P}$
a forcing notion. If
$\mathbb {P}$
a forcing notion. If
![]() $\mathcal {I}\leq _{\textsf {K}}\mathcal {J}$
and
$\mathcal {I}\leq _{\textsf {K}}\mathcal {J}$
and
![]() $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
![]() $\mathcal {J},$
then
$\mathcal {J},$
then
![]() $\mathbb {P}$
also destroys
$\mathbb {P}$
also destroys
![]() $\mathcal {I}.$
$\mathcal {I}.$
By
![]() $\mathbb {C}$
we will denote Cohen forcing. There is a nice characterization of Cohen indestructibility. By nwd we denote the ideal of all nowhere dense subsets of the rational numbers. We have the following:
$\mathbb {C}$
we will denote Cohen forcing. There is a nice characterization of Cohen indestructibility. By nwd we denote the ideal of all nowhere dense subsets of the rational numbers. We have the following:
Proposition 18 [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44].
Let
![]() $\mathcal {I}$
be an ideal. The following are equivalent
$\mathcal {I}$
be an ideal. The following are equivalent
![]() $:$
$:$
-
1.
 $\mathcal {I}$
is
$\mathcal {I}$
is
 $\mathbb {C}$
-destructible.
$\mathbb {C}$
-destructible. -
2.
 $\mathcal {I}\leq _{\textsf {K}}$
nwd.
$\mathcal {I}\leq _{\textsf {K}}$
nwd.
More results of this type can be found in [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44]. It is easy to see that tight MAD families are
![]() $\mathbb {C} $
-indestructible. The converse does not hold (in fact,
$\mathbb {C} $
-indestructible. The converse does not hold (in fact,
![]() $\mathbb {C} $
-indestructibility does not even imply weak tightness). However, this two notions are very related:
$\mathbb {C} $
-indestructibility does not even imply weak tightness). However, this two notions are very related:
Proposition 19 [Reference Hrušák and Ferreira40, Reference Kurilić51].
Let
![]() $\mathcal {A}$
be a MAD family. If
$\mathcal {A}$
be a MAD family. If
![]() $\mathcal {A}$
is Cohen indestructible, then there is
$\mathcal {A}$
is Cohen indestructible, then there is
![]() $X\in \mathcal {I(A)}^{+}$
such that
$X\in \mathcal {I(A)}^{+}$
such that
![]() $\mathcal {A}\upharpoonright X$
is tight.
$\mathcal {A}\upharpoonright X$
is tight.
In particular, there is a
![]() $\mathbb {C}$
-indestructible MAD family if and only if there is a tight MAD family.
$\mathbb {C}$
-indestructible MAD family if and only if there is a tight MAD family.
Definition 20. Let
![]() $X,Y$
be countable sets,
$X,Y$
be countable sets,
![]() $\mathcal {A}$
a MAD family in X and
$\mathcal {A}$
a MAD family in X and
![]() $\mathcal {B}$
a MAD family in
$\mathcal {B}$
a MAD family in
![]() $Y.$
$Y.$
-
1. Let
 $g:Y\longrightarrow X$
be a function. We say that g is a strong Katětov function from
$g:Y\longrightarrow X$
be a function. We say that g is a strong Katětov function from
 $(Y,\mathcal {B})$
to
$(Y,\mathcal {B})$
to
 $(X,\mathcal {A})$
if g is a Katětov function from
$(X,\mathcal {A})$
if g is a Katětov function from
 $(Y,\mathcal {B})$
to
$(Y,\mathcal {B})$
to
 $(X,\mathcal {A})$
and for every
$(X,\mathcal {A})$
and for every
 $B\in \mathcal {I}\left ( B\right ) ,$
we have that
$B\in \mathcal {I}\left ( B\right ) ,$
we have that
 $g\left [ B\right ] \in \mathcal {I}(\mathcal {A}).$
$g\left [ B\right ] \in \mathcal {I}(\mathcal {A}).$
-
2. We say that
 $\mathcal {A} \leq _{\textsf {SK}}\mathcal {B}$
if there is a strong Katětov function from
$\mathcal {A} \leq _{\textsf {SK}}\mathcal {B}$
if there is a strong Katětov function from
 $(Y,\mathcal {B})$
to
$(Y,\mathcal {B})$
to
 $(X,\mathcal {A}).$
$(X,\mathcal {A}).$
In spite of the name, the order
![]() $\leq _{\textsf {SK}}$
is not that much different than
$\leq _{\textsf {SK}}$
is not that much different than
![]() $\leq _{\textsf {K}}$
when working with weakly tight MAD families, as will be explained in the lemma below. All the relevant ideas are already contained (at least implicitly) in [Reference Hrušák and Ferreira40].
$\leq _{\textsf {K}}$
when working with weakly tight MAD families, as will be explained in the lemma below. All the relevant ideas are already contained (at least implicitly) in [Reference Hrušák and Ferreira40].
Lemma 21. Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be two MAD families on
$\mathcal {B}$
be two MAD families on
![]() $\omega .$
$\omega .$
-
1. If
 $X\in \mathcal {I(A)}^{\ast },$
then
$X\in \mathcal {I(A)}^{\ast },$
then
 $\mathcal {A}\upharpoonright X$
and
$\mathcal {A}\upharpoonright X$
and
 $\mathcal {A}$
are Katětov equivalent.
$\mathcal {A}$
are Katětov equivalent. -
2. If f is a Katětov function from
 $(\omega ,\mathcal {B})$
to
$(\omega ,\mathcal {B})$
to
 $(\omega ,\mathcal {A}),$
then the set
$(\omega ,\mathcal {A}),$
then the set
 $\{B\in \mathcal {B}\mid f\left [ B\right ] \in \left [ \omega \right ] ^{<\omega }\}$
is finite.
$\{B\in \mathcal {B}\mid f\left [ B\right ] \in \left [ \omega \right ] ^{<\omega }\}$
is finite. -
3. If
 $\mathcal {A}\leq _{\textsf {K}}\mathcal {B},$
then there is
$\mathcal {A}\leq _{\textsf {K}}\mathcal {B},$
then there is
 $X\in \mathcal {I(B)}^{\ast }$
and a Katětov function f from
$X\in \mathcal {I(B)}^{\ast }$
and a Katětov function f from
 $(X,\mathcal {B}\upharpoonright X)$
to
$(X,\mathcal {B}\upharpoonright X)$
to
 $(\omega ,\mathcal {A})$
such that if
$(\omega ,\mathcal {A})$
such that if
 $B\in \mathcal {B}\upharpoonright X,$
then
$B\in \mathcal {B}\upharpoonright X,$
then
 $f\left [ B\right ] $
is infinite (recall that
$f\left [ B\right ] $
is infinite (recall that
 $\mathcal {B}\upharpoonright X=_{\textsf {K}}\mathcal {B}$
by the first point).
$\mathcal {B}\upharpoonright X=_{\textsf {K}}\mathcal {B}$
by the first point). -
4. If g is a Katětov function from
 $(\omega ,\mathcal {B})$
to
$(\omega ,\mathcal {B})$
to
 $(\omega ,\mathcal {A})$
and
$(\omega ,\mathcal {A})$
and
 $\mathcal {A}$
is weakly tight, then the set
$\mathcal {A}$
is weakly tight, then the set
 $\{B\in \mathcal {B}\mid f[B]\in \mathcal {I(A)}^{+}\}$
is finite.
$\{B\in \mathcal {B}\mid f[B]\in \mathcal {I(A)}^{+}\}$
is finite. -
5. If
 $\mathcal {A}\leq _{\textsf {K}}\mathcal {B}$
and
$\mathcal {A}\leq _{\textsf {K}}\mathcal {B}$
and
 $\mathcal {A}$
is weakly tight, then there is a MAD family
$\mathcal {A}$
is weakly tight, then there is a MAD family
 $\mathcal {B}_{1}$
such that
$\mathcal {B}_{1}$
such that
 $\mathcal {B}=_{\textsf {K}}\mathcal {B}_{1}$
and
$\mathcal {B}=_{\textsf {K}}\mathcal {B}_{1}$
and
 $\mathcal {A} \leq _{\textsf {SK}}\mathcal {B}_{1}.$
$\mathcal {A} \leq _{\textsf {SK}}\mathcal {B}_{1}.$
Proof We start with the first point. Let
![]() $X\in \mathcal {I(A)}^{\ast },$
we only need to prove that
$X\in \mathcal {I(A)}^{\ast },$
we only need to prove that
![]() $\mathcal {A}\upharpoonright X \leq _{\textsf {K}} \mathcal {A}$
(see Lemma 10). Choose n any point in
$\mathcal {A}\upharpoonright X \leq _{\textsf {K}} \mathcal {A}$
(see Lemma 10). Choose n any point in
![]() $X.$
Define
$X.$
Define
![]() $f:\omega \longrightarrow X$
where
$f:\omega \longrightarrow X$
where
![]() $f\upharpoonright X$
is the identity and
$f\upharpoonright X$
is the identity and
![]() $f\upharpoonright (\omega \setminus X)$
is constant
$f\upharpoonright (\omega \setminus X)$
is constant
![]() $n.$
This is a Katětov function from
$n.$
This is a Katětov function from
![]() $(\omega ,\mathcal {A})$
to
$(\omega ,\mathcal {A})$
to
![]() $(X,\mathcal {A} \upharpoonright X).$
$(X,\mathcal {A} \upharpoonright X).$
For the second point, assume that there are distinct
![]() $B_{0},B_{1} ,\dots \in \mathcal {B}$
such that
$B_{0},B_{1} ,\dots \in \mathcal {B}$
such that
![]() $f\left [ B_{n}\right ] $
is finite for every
$f\left [ B_{n}\right ] $
is finite for every
![]() $n\in \omega .$
For each
$n\in \omega .$
For each
![]() $n\in \omega ,$
choose
$n\in \omega ,$
choose
![]() $b_{n}\in f\left [ B_{n}\right ] $
such that
$b_{n}\in f\left [ B_{n}\right ] $
such that
![]() $f^{-1}\left ( \left \{ b_{n}\right \} \right ) \cap B_{n}$
is infinite. Let
$f^{-1}\left ( \left \{ b_{n}\right \} \right ) \cap B_{n}$
is infinite. Let
![]() $S=\left \{ b_{n}\mid n\in \omega \right \} .$
If S is finite, then
$S=\left \{ b_{n}\mid n\in \omega \right \} .$
If S is finite, then
![]() $f^{-1}\left ( S\right ) \in \mathcal {I(B)}^{+},$
which is a contradiction. If S is infinite, find
$f^{-1}\left ( S\right ) \in \mathcal {I(B)}^{+},$
which is a contradiction. If S is infinite, find
![]() $A\in \mathcal {A}$
such that
$A\in \mathcal {A}$
such that
![]() $A\cap S$
is infinite. It follows that
$A\cap S$
is infinite. It follows that
![]() $f^{-1}\left ( A\right ) \in \mathcal {I(B)}^{+},$
which is also a contradiction.
$f^{-1}\left ( A\right ) \in \mathcal {I(B)}^{+},$
which is also a contradiction.
We now prove the third point. Let
![]() $\mathcal {A}\leq _ {\textsf {K}} \mathcal {B}$
and choose f a Katětov function from
$\mathcal {A}\leq _ {\textsf {K}} \mathcal {B}$
and choose f a Katětov function from
![]() $(\omega ,\mathcal {B})$
to
$(\omega ,\mathcal {B})$
to
![]() $(\omega ,\mathcal {A}).$
Let
$(\omega ,\mathcal {A}).$
Let
![]() $D=\bigcup \{B\in \mathcal {B}\mid f\left [ B\right ] \in \left [ \omega \right ] ^{<\omega }\}$
which we know is in
$D=\bigcup \{B\in \mathcal {B}\mid f\left [ B\right ] \in \left [ \omega \right ] ^{<\omega }\}$
which we know is in
![]() $\mathcal {I(B)}$
by the previous point. Define
$\mathcal {I(B)}$
by the previous point. Define
![]() $X=\omega \setminus D$
and consider the restriction of f to
$X=\omega \setminus D$
and consider the restriction of f to
![]() $X.$
$X.$
We now prove point 4. Assume that there are distinct
![]() $B_{0},B_{1} ,\dots \in \mathcal {B}$
such that
$B_{0},B_{1} ,\dots \in \mathcal {B}$
such that
![]() $f\left [ B_{n}\right ] \in \mathcal {I(A)}^{+}$
for every
$f\left [ B_{n}\right ] \in \mathcal {I(A)}^{+}$
for every
![]() $n\in \omega .$
Since
$n\in \omega .$
Since
![]() $\mathcal {A}$
is weakly tight, there is
$\mathcal {A}$
is weakly tight, there is
![]() $A\in \mathcal {I(A)}$
such that
$A\in \mathcal {I(A)}$
such that
![]() $A\cap f[B_{n}]$
is infinite for infinitely many
$A\cap f[B_{n}]$
is infinite for infinitely many
![]() $n\in \omega .$
It follows that
$n\in \omega .$
It follows that
![]() $f^{-1}\left ( A\right ) \in \mathcal {I(B)} ^{+},$
which is a contradiction.
$f^{-1}\left ( A\right ) \in \mathcal {I(B)} ^{+},$
which is a contradiction.
The last point follows with the same argument as the one of point 3, but using point 4 instead of point 2.
We now review the notion of trace ideal. Define the mapping
![]() $\pi :\mathcal {P}\left ( 2^{<\omega }\right ) \longrightarrow \mathcal {P}\left ( 2^{\omega }\right ) $
as
$\pi :\mathcal {P}\left ( 2^{<\omega }\right ) \longrightarrow \mathcal {P}\left ( 2^{\omega }\right ) $
as
![]() $\pi \left ( a\right ) =\{x\in 2^{\omega }\mid \exists ^{\infty }s\in a\left ( s\subseteq x\right ) \}.$
It is not hard to see that
$\pi \left ( a\right ) =\{x\in 2^{\omega }\mid \exists ^{\infty }s\in a\left ( s\subseteq x\right ) \}.$
It is not hard to see that
![]() $\pi \left ( a\right ) $
is always a
$\pi \left ( a\right ) $
is always a
![]() $G_{\delta }$
-set. If
$G_{\delta }$
-set. If
![]() $\mathcal {K}$
is a
$\mathcal {K}$
is a
![]() $\sigma $
-ideal on
$\sigma $
-ideal on
![]() $2^{\omega },$
its trace ideal is defined as tr(
$2^{\omega },$
its trace ideal is defined as tr(
![]() $\mathcal {K}$
)
$\mathcal {K}$
)
![]() $=\{a\subseteq 2^{\omega }\mid \pi \left ( a\right ) \in \mathcal {K}\}.$
Trace ideals are fundamental in the study of forcing indestructibility. It is interesting that the indestructibility of the most important forcing notions can be characterized using the Katětov order and trace ideals. The reader may consult [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44] to learn about this. The trace ideals will not be needed until Section 6 and in there we will review the results needed for this paper.
$=\{a\subseteq 2^{\omega }\mid \pi \left ( a\right ) \in \mathcal {K}\}.$
Trace ideals are fundamental in the study of forcing indestructibility. It is interesting that the indestructibility of the most important forcing notions can be characterized using the Katětov order and trace ideals. The reader may consult [Reference Brendle and Yatabe9, Reference Hrušák and Zapletal44] to learn about this. The trace ideals will not be needed until Section 6 and in there we will review the results needed for this paper.
4 Katětov-top MAD families vs.
 $\mathfrak {s\leq b}$
$\mathfrak {s\leq b}$
We say a MAD family
![]() $\mathcal {A}$
is Katětov-top if
$\mathcal {A}$
is Katětov-top if
![]() $\mathcal {A}$
is Katětov above every other MAD family. This notion was first consider by García-Ferreira and Hrušák in [Reference Hrušák and Ferreira40], where they proved that such families do not exist assuming
$\mathcal {A}$
is Katětov above every other MAD family. This notion was first consider by García-Ferreira and Hrušák in [Reference Hrušák and Ferreira40], where they proved that such families do not exist assuming
![]() $\mathfrak {b=c}.$
The purpose of this section is to improve this result.
$\mathfrak {b=c}.$
The purpose of this section is to improve this result.
A Katětov-top MAD family would have really strong combinatorial properties:
Lemma 22. Let
![]() $\mathcal {A}$
be a Katětov-top MAD family and
$\mathcal {A}$
be a Katětov-top MAD family and
![]() $\mathbb {P}$
a partial order.
$\mathbb {P}$
a partial order.
-
1. The size of
 $\mathcal {A}$
is
$\mathcal {A}$
is
 $\mathfrak {a}.$
$\mathfrak {a}.$
-
2. If there is a weakly tight MAD family, then
 $\mathcal {A}$
is weakly tight.
$\mathcal {A}$
is weakly tight. -
3. If there is a tight MAD family, then
 $\mathcal {A}$
is tight.
$\mathcal {A}$
is tight. -
4. If
 $\mathbb {P}$
destroys
$\mathbb {P}$
destroys
 $\mathcal {A},$
then
$\mathcal {A},$
then
 $\mathbb {P}$
destroys every other MAD family.
$\mathbb {P}$
destroys every other MAD family. -
5. If there is a
 $\mathbb {P}$
-indestructible MAD family, then
$\mathbb {P}$
-indestructible MAD family, then
 $\mathcal {A}$
is
$\mathcal {A}$
is
 $\mathbb {P}$
-indestructible.
$\mathbb {P}$
-indestructible.
It is the common belief that Katětov-top MAD families should not exist, yet we only have partial answers. In this section, we will prove that the cardinal invariant inequality
![]() $\mathfrak {s\leq b}$
implies that there are no Katětov-top MAD families. In fact, we will prove even more. Informally speaking, we will prove that if we “know how to construct a weakly tight completely separable MAD family,” then we can show that there are no Katětov-top MAD families. In order to formalize this statement, we need the following definition:
$\mathfrak {s\leq b}$
implies that there are no Katětov-top MAD families. In fact, we will prove even more. Informally speaking, we will prove that if we “know how to construct a weakly tight completely separable MAD family,” then we can show that there are no Katětov-top MAD families. In order to formalize this statement, we need the following definition:
Definition 23. Let
![]() $\mathbb {P}$
be a partial order. We say that
$\mathbb {P}$
be a partial order. We say that
![]() $\mathbb {P}$
is a forcing notion for a weakly tight family if the following conditions hold
$\mathbb {P}$
is a forcing notion for a weakly tight family if the following conditions hold
![]() $:$
$:$
-
1. If
 $p\in \mathbb {P},$
then p is of the form
$p\in \mathbb {P},$
then p is of the form
 $p=(\mathcal {A}_{p},R_{p})$
where
$p=(\mathcal {A}_{p},R_{p})$
where
 $\mathcal {A}_{p}$
is an AD family with
$\mathcal {A}_{p}$
is an AD family with
 $\left \vert \mathcal {A}_{p}\right \vert <\mathfrak {c}$
and
$\left \vert \mathcal {A}_{p}\right \vert <\mathfrak {c}$
and
 $R_{p}\in $
H
$R_{p}\in $
H
 $\left ( \mathfrak {c}^{+}\right ) .$
Footnote
3
$\left ( \mathfrak {c}^{+}\right ) .$
Footnote
3
-
2. If
 $p\leq q,$
then
$p\leq q,$
then
 $\mathcal {A}_{q}\subseteq \mathcal {A}_{p}.$
$\mathcal {A}_{q}\subseteq \mathcal {A}_{p}.$
-
3. (
 $\mathfrak {c}$
-closed) Let
$\mathfrak {c}$
-closed) Let
 $\kappa <\mathfrak {c}.$
If
$\kappa <\mathfrak {c}.$
If
 $\left \{ p_{\alpha }\mid \alpha <\kappa \right \} \subseteq \mathbb {P}$
is a decreasing sequence and
$\left \{ p_{\alpha }\mid \alpha <\kappa \right \} \subseteq \mathbb {P}$
is a decreasing sequence and
 $\mathcal {B}=\bigcup \limits _{\alpha <\kappa }\mathcal {A} _{p_{\alpha }}$
has size less than
$\mathcal {B}=\bigcup \limits _{\alpha <\kappa }\mathcal {A} _{p_{\alpha }}$
has size less than
 $\mathfrak {c},$
then there is a condition
$\mathfrak {c},$
then there is a condition
 $q=(\mathcal {B},R)\in \mathbb {P}$
such that
$q=(\mathcal {B},R)\in \mathbb {P}$
such that
 $q\leq p_{\alpha }$
for every
$q\leq p_{\alpha }$
for every
 $\alpha <\kappa .$
$\alpha <\kappa .$
-
4. For every
 $p\in \mathbb {P}$
and
$p\in \mathbb {P}$
and
 $X\in \mathcal {I(A}_{p}\mathcal {)}^{+},$
there is
$X\in \mathcal {I(A}_{p}\mathcal {)}^{+},$
there is
 $q\in \mathbb {P}$
with the following properties
$q\in \mathbb {P}$
with the following properties
 $:$
$:$
-
(a)
 $q\leq p.$
$q\leq p.$
-
(b)
 $\left \vert \mathcal {A}_{q}\right \vert \leq \left \vert \mathcal {A} _{p}\right \vert +\omega .$
$\left \vert \mathcal {A}_{q}\right \vert \leq \left \vert \mathcal {A} _{p}\right \vert +\omega .$
-
(c) There are
 $A_{0}, A_{1},\dots \in \mathcal {A}_{q}\setminus \mathcal {A}_{p}$
pairwise distinct such that
$A_{0}, A_{1},\dots \in \mathcal {A}_{q}\setminus \mathcal {A}_{p}$
pairwise distinct such that
 $A_{n}\subseteq X$
for every
$A_{n}\subseteq X$
for every
 $n\in \omega .$
$n\in \omega .$
-
-
5. For every
 $p\in \mathbb {P}$
and
$p\in \mathbb {P}$
and
 $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \mathcal {I(A}_{p}\mathcal {)}^{+},$
there is
$\left \{ X_{n}\mid n\in \omega \right \} \subseteq \mathcal {I(A}_{p}\mathcal {)}^{+},$
there is
 $q\in \mathbb {P}$
such that
$q\in \mathbb {P}$
such that
 $:$
$:$
-
(a)
 $q\leq p.$
$q\leq p.$
-
(b)
 $\left \vert \mathcal {A}_{q}\right \vert \leq \left \vert \mathcal {A} _{p}\right \vert +\omega .$
$\left \vert \mathcal {A}_{q}\right \vert \leq \left \vert \mathcal {A} _{p}\right \vert +\omega .$
-
(c) There is
 $A\in \mathcal {I(A}_{q}\mathcal {)}$
such that there are infinitely many
$A\in \mathcal {I(A}_{q}\mathcal {)}$
such that there are infinitely many
 $n\in \omega $
for which
$n\in \omega $
for which
 $\left \vert X_{n}\cap A\right \vert =\omega .$
$\left \vert X_{n}\cap A\right \vert =\omega .$
-
Let
![]() $p=(\mathcal {A}_{p},R_{p})$
be an element of
$p=(\mathcal {A}_{p},R_{p})$
be an element of
![]() $\mathbb {P}.$
The purpose of
$\mathbb {P}.$
The purpose of
![]() $R_{p}$
is simply to be a parameter, probably needed to define
$R_{p}$
is simply to be a parameter, probably needed to define
![]() $\leq $
(or to be used in a recursive construction). It is worth pointing out that while
$\leq $
(or to be used in a recursive construction). It is worth pointing out that while
![]() $p\leq q$
implies
$p\leq q$
implies
![]() $\mathcal {A}_{q}\subseteq \mathcal {A}_{p},$
in general the converse does not need to hold. Note that by Point 4 above,
$\mathcal {A}_{q}\subseteq \mathcal {A}_{p},$
in general the converse does not need to hold. Note that by Point 4 above,
![]() $\mathcal {A}_{p}$
is a nowhere MAD family.
$\mathcal {A}_{p}$
is a nowhere MAD family.
Intuitively, the definition tries to formalize the idea that we “know a method to recursively construct a completely separable weakly tight MAD family.” It is trivial to build a completely separable weakly tight MAD family assuming the existence of a forcing notion for a weakly tight family. It is easy to see that the proofs of Proposition 14 (see [Reference Hrušák36, Reference Kurilić51]) in fact show that
![]() $\mathfrak {b=c}$
imply that there is a forcing notion for a weakly tight family (in fact, in this case we can take
$\mathfrak {b=c}$
imply that there is a forcing notion for a weakly tight family (in fact, in this case we can take
![]() $\mathbb {P}$
to be the set of all AD families of size less than
$\mathbb {P}$
to be the set of all AD families of size less than
![]() $\mathfrak {c},$
ordered by reverse inclusion. There is no need of the parameters mentioned in the first point of Definition 23). The proof of Theorem 13 actually shows that
$\mathfrak {c},$
ordered by reverse inclusion. There is no need of the parameters mentioned in the first point of Definition 23). The proof of Theorem 13 actually shows that
![]() $\mathfrak {s\leq b}$
implies that there is a forcing notion for a weakly tight family (this time, the description of the forcing is more elaborated than in the case of
$\mathfrak {s\leq b}$
implies that there is a forcing notion for a weakly tight family (this time, the description of the forcing is more elaborated than in the case of
![]() $\mathfrak {b=c},$
but the reader familiar with [Reference Raghavan and Steprāns59] will have no problem extracting the forcing notion from the proof of the main theorem of the paper). It is currently unknown if ZFC proves that there is a forcing notion for a weakly tight family. The reader may consult [Reference Corral and Hrušák16] for another application of
$\mathfrak {b=c},$
but the reader familiar with [Reference Raghavan and Steprāns59] will have no problem extracting the forcing notion from the proof of the main theorem of the paper). It is currently unknown if ZFC proves that there is a forcing notion for a weakly tight family. The reader may consult [Reference Corral and Hrušák16] for another application of
![]() $\mathfrak {s\leq b}$
to MAD families.
$\mathfrak {s\leq b}$
to MAD families.
We will now prove that there is no Katětov-top MAD family if there is a forcing notion for a weakly tight family. We start with the following lemma:
Lemma 24. Let
![]() $\mathbb {P}$
be a forcing notion for a weakly tight family,
$\mathbb {P}$
be a forcing notion for a weakly tight family,
![]() $\mathcal {B}$
a MAD family,
$\mathcal {B}$
a MAD family,
![]() $p=(\mathcal {A}_{p},R_{p})\in \mathbb {P}$
and
$p=(\mathcal {A}_{p},R_{p})\in \mathbb {P}$
and
![]() $h\in \omega ^{\omega }$
an injective function. There is
$h\in \omega ^{\omega }$
an injective function. There is
![]() $q\in \mathbb {P}$
with the following properties
$q\in \mathbb {P}$
with the following properties
![]() $:$
$:$
-
1.
 $q\leq p.$
$q\leq p.$
-
2.
 $\left \vert \mathcal {A}_{q}\right \vert \leq \left \vert \mathcal {A} _{p}\right \vert +\omega .$
$\left \vert \mathcal {A}_{q}\right \vert \leq \left \vert \mathcal {A} _{p}\right \vert +\omega .$
-
3. If
 $\mathcal {D}$
is any MAD family with
$\mathcal {D}$
is any MAD family with
 $\mathcal {A} _{q}\subseteq \mathcal {D},$
then h is not a strong Katětov function from
$\mathcal {A} _{q}\subseteq \mathcal {D},$
then h is not a strong Katětov function from
 $(\omega ,\mathcal {B})$
to
$(\omega ,\mathcal {B})$
to
 $(\omega ,\mathcal {D}).$
$(\omega ,\mathcal {D}).$
Proof If h is not a Katětov function from
![]() $(\omega ,\mathcal {B})$
to
$(\omega ,\mathcal {B})$
to
![]() $(\omega ,\mathcal {A}_{p}),$
there is nothing to do, so we assume it is. We know that
$(\omega ,\mathcal {A}_{p}),$
there is nothing to do, so we assume it is. We know that
![]() $h\left [ \omega \right ] \in \mathcal {I(A}_{p}\mathcal {)}^{+}$
and since
$h\left [ \omega \right ] \in \mathcal {I(A}_{p}\mathcal {)}^{+}$
and since
![]() $\mathcal {A}_{p}$
is nowhere MAD, there is an infinite
$\mathcal {A}_{p}$
is nowhere MAD, there is an infinite
![]() $Y\subseteq h\left [ \omega \right ] $
with
$Y\subseteq h\left [ \omega \right ] $
with
![]() $Y\in \mathcal {A}_{p}^{\perp }.$
Since h is injective, it follows that
$Y\in \mathcal {A}_{p}^{\perp }.$
Since h is injective, it follows that
![]() $h^{-1}\left ( Y\right ) $
is infinite. Since
$h^{-1}\left ( Y\right ) $
is infinite. Since
![]() $\mathcal {B}$
is maximal, we can find and infinite
$\mathcal {B}$
is maximal, we can find and infinite
![]() $W\in \mathcal {I(B)}$
contained in
$W\in \mathcal {I(B)}$
contained in
![]() $h^{-1}\left ( Y\right ) .$
$h^{-1}\left ( Y\right ) .$
By Point 4 of Definition 23, we can find
![]() $q\leq p$
such that
$q\leq p$
such that
![]() $\left \vert \mathcal {A}_{q}\right \vert \leq \left \vert \mathcal {A}_{p}\right \vert +\omega $
and
$\left \vert \mathcal {A}_{q}\right \vert \leq \left \vert \mathcal {A}_{p}\right \vert +\omega $
and
![]() $h\left [ W\right ] $
contains infinitely many elements of
$h\left [ W\right ] $
contains infinitely many elements of
![]() $\mathcal {A} _{q}.$
In this way,
$\mathcal {A} _{q}.$
In this way,
![]() $h\left [ W\right ] \in \mathcal {I}\left ( \mathcal {A} _{q}\right ) ^{++}.$
It follows that if
$h\left [ W\right ] \in \mathcal {I}\left ( \mathcal {A} _{q}\right ) ^{++}.$
It follows that if
![]() $\mathcal {D}$
is any MAD family extending
$\mathcal {D}$
is any MAD family extending
![]() $\mathcal {A}_{q},$
then
$\mathcal {A}_{q},$
then
![]() $h\left [ W\right ] \in \mathcal {I}\left ( \mathcal {D}\right ) ^{+}$
, so h is not a strong Katětov function from
$h\left [ W\right ] \in \mathcal {I}\left ( \mathcal {D}\right ) ^{+}$
, so h is not a strong Katětov function from
![]() $(\omega ,\mathcal {B})$
to
$(\omega ,\mathcal {B})$
to
![]() $(\omega ,\mathcal {D}).$
$(\omega ,\mathcal {D}).$
The following is a well-known and very useful theorem of Mathias:
Theorem 25 (Mathias [Reference Mathias54]).
Let
![]() $\mathcal {A}$
be a MAD family and
$\mathcal {A}$
be a MAD family and
![]() $f\in \omega ^{\omega }.$
There is
$f\in \omega ^{\omega }.$
There is
![]() $X\in \mathcal {I}^{+}(\mathcal {A})$
such that either
$X\in \mathcal {I}^{+}(\mathcal {A})$
such that either
![]() $f\upharpoonright X$
is constant or
$f\upharpoonright X$
is constant or
![]() $f\upharpoonright X$
is injective.
$f\upharpoonright X$
is injective.
The proof of the following lemma is nearly identical to the one of Proposition 3.7 of [Reference Hrušák and Ferreira40]:
Lemma 26. Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be MAD families with
$\mathcal {B}$
be MAD families with
![]() $\mathcal {A}$
weakly tight. If
$\mathcal {A}$
weakly tight. If
![]() $\mathcal {A}\leq _{\textsf {K}} \mathcal {B},$
then there are X and h with the following properties
$\mathcal {A}\leq _{\textsf {K}} \mathcal {B},$
then there are X and h with the following properties
![]() $:$
$:$
-
1.
 $X\in \mathcal {I(B)}^{+}.$
$X\in \mathcal {I(B)}^{+}.$
-
2.
 $h:X\longrightarrow \omega $
is injective and a strong Katětov function from
$h:X\longrightarrow \omega $
is injective and a strong Katětov function from
 $(X,\mathcal {B}\upharpoonright X)$
to
$(X,\mathcal {B}\upharpoonright X)$
to
 $(\omega ,\mathcal {A} ).$
$(\omega ,\mathcal {A} ).$
Proof Let
![]() $f\in \omega ^{\omega }$
be a Katětov function from
$f\in \omega ^{\omega }$
be a Katětov function from
![]() $(\omega ,\mathcal {B})$
to
$(\omega ,\mathcal {B})$
to
![]() $(\omega ,\mathcal {A}).$
By the theorem of Mathias above, we can find
$(\omega ,\mathcal {A}).$
By the theorem of Mathias above, we can find
![]() $X_{0}\in \mathcal {I(B)}^{+}$
such that either
$X_{0}\in \mathcal {I(B)}^{+}$
such that either
![]() $f\upharpoonright X_{0}$
is constant or
$f\upharpoonright X_{0}$
is constant or
![]() $f\upharpoonright X_{0}$
is injective. However, the former case can not occur, since
$f\upharpoonright X_{0}$
is injective. However, the former case can not occur, since
![]() $X_{0}\in \mathcal {I(B)}^{+}$
and f is a Katětov function. Note that
$X_{0}\in \mathcal {I(B)}^{+}$
and f is a Katětov function. Note that
![]() $f\upharpoonright X_{0}$
is an injective Katětov function form
$f\upharpoonright X_{0}$
is an injective Katětov function form
![]() $(X_{0},X_{0}\upharpoonright \mathcal {B})$
to
$(X_{0},X_{0}\upharpoonright \mathcal {B})$
to
![]() $(\omega ,\mathcal {A}).$
$(\omega ,\mathcal {A}).$
Let
![]() $L=\{B\in \mathcal {B}\mid f\left [ B\right ] \in \mathcal {I(A)}^{+}\}.$
Since
$L=\{B\in \mathcal {B}\mid f\left [ B\right ] \in \mathcal {I(A)}^{+}\}.$
Since
![]() $\mathcal {A}$
is weakly tight, by Point 4 of Lemma 21, we know that L is a finite set. Let
$\mathcal {A}$
is weakly tight, by Point 4 of Lemma 21, we know that L is a finite set. Let
![]() $X=X_{0} \setminus \bigcup L$
and
$X=X_{0} \setminus \bigcup L$
and
![]() $h=f\upharpoonright X.$
It is clear that X and h have the desired properties.
$h=f\upharpoonright X.$
It is clear that X and h have the desired properties.
We can now prove the main theorem of the section:
Theorem 27. If there is a forcing notion for a weakly tight family, then there are no Katětov-top MAD families.
Proof Fix
![]() $\mathbb {P}$
a forcing notion for a weakly tight family and
$\mathbb {P}$
a forcing notion for a weakly tight family and
![]() $\mathcal {B}$
a MAD family. Using
$\mathcal {B}$
a MAD family. Using
![]() $\mathbb {P},$
we will find a MAD family that is not Katětov below
$\mathbb {P},$
we will find a MAD family that is not Katětov below
![]() $\mathcal {B}.$
With the aid of Lemma 24 and a careful bookkeeping device, we can build a MAD family
$\mathcal {B}.$
With the aid of Lemma 24 and a careful bookkeeping device, we can build a MAD family
![]() $\mathcal {A}$
with the following properties:
$\mathcal {A}$
with the following properties:
-
1.
 $\mathcal {A}$
is completely separable and weakly tight.
$\mathcal {A}$
is completely separable and weakly tight. -
2. For every
 $X\in \mathcal {I(B)}^{+}$
and an injective
$X\in \mathcal {I(B)}^{+}$
and an injective
 $h:X\longrightarrow \omega ,$
we have that h is not a strong Katětov function from
$h:X\longrightarrow \omega ,$
we have that h is not a strong Katětov function from
 $(X,\mathcal {B}\upharpoonright X)$
to
$(X,\mathcal {B}\upharpoonright X)$
to
 $(\omega ,\mathcal {A}).$
$(\omega ,\mathcal {A}).$
In this way,
![]() $\mathcal {A}$
is a weakly tight MAD family such that for every
$\mathcal {A}$
is a weakly tight MAD family such that for every
![]() $X\in \mathcal {I(B)}^{+},$
there is no injective strong Katětov function from
$X\in \mathcal {I(B)}^{+},$
there is no injective strong Katětov function from
![]() $(X,\mathcal {B}\upharpoonright X)$
to
$(X,\mathcal {B}\upharpoonright X)$
to
![]() $(\omega ,\mathcal {A}).$
By Lemma 26, it follows
$(\omega ,\mathcal {A}).$
By Lemma 26, it follows
![]() $\mathcal {A}$
is not Katětov below
$\mathcal {A}$
is not Katětov below
![]() $\mathcal {B}.$
$\mathcal {B}.$
As mentioned before, by Theorem 13 and a comment above, we get the following:
Corollary 28. If
![]() $\mathfrak {s\leq b},$
then there are no Katětov-top MAD families.
$\mathfrak {s\leq b},$
then there are no Katětov-top MAD families.
Recall from the introduction that García-Ferreira and Hrušák proved a similar theorem assuming
![]() $\mathfrak {b=c}$
(see [Reference Hrušák and Ferreira40]), so our result generalizes theirs. It is worth mentioning that Raghavan has extended the work in [Reference Raghavan and Steprāns59] and obtain weakly tight MAD families in models of
$\mathfrak {b=c}$
(see [Reference Hrušák and Ferreira40]), so our result generalizes theirs. It is worth mentioning that Raghavan has extended the work in [Reference Raghavan and Steprāns59] and obtain weakly tight MAD families in models of
![]() $\mathfrak {b<s}.$
In fact, he proved under
$\mathfrak {b<s}.$
In fact, he proved under
![]() $\mathfrak {b<s,}$
that if certain “PCF hypothesis” are true, then weakly tight MAD families exist. It is very likely that his arguments actually show that there is a forcing notion for a weakly tight family under those assumptions. Unfortunately, the theorems of Raghavan remain unpublished. It is our hope that someday, the need for the extra hypothesis in the case
$\mathfrak {b<s,}$
that if certain “PCF hypothesis” are true, then weakly tight MAD families exist. It is very likely that his arguments actually show that there is a forcing notion for a weakly tight family under those assumptions. Unfortunately, the theorems of Raghavan remain unpublished. It is our hope that someday, the need for the extra hypothesis in the case
![]() $\mathfrak {b<s}$
will be eliminated, providing both a ZFCconstruction of a weakly tight completely separable MAD family and a proof that there are no Katětov-top MAD families.
$\mathfrak {b<s}$
will be eliminated, providing both a ZFCconstruction of a weakly tight completely separable MAD family and a proof that there are no Katětov-top MAD families.
5 A Katětov maximal MAD family from
 $\mathfrak {b=c}$
$\mathfrak {b=c}$
A MAD family
![]() $\mathcal {A}$
is Katětov maximal if there is no MAD family that is strictly above
$\mathcal {A}$
is Katětov maximal if there is no MAD family that is strictly above
![]() $\mathcal {A}$
in the Katětov order. Obviously, a Katětov-top MAD family would be Katětov maximal. However, unlike the case of Katětov-top MAD families, we know that Katětov maximal MAD families may consistently exist. This was first proved by Arciga, Hrušák, and Martínez in [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1]. In fact, they proved that
$\mathcal {A}$
in the Katětov order. Obviously, a Katětov-top MAD family would be Katětov maximal. However, unlike the case of Katětov-top MAD families, we know that Katětov maximal MAD families may consistently exist. This was first proved by Arciga, Hrušák, and Martínez in [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1]. In fact, they proved that
![]() $\mathfrak {t=c}$
implies that there is a Katětov maximal MAD family. We will now improve this result. Our method is a refinement of theirs. Although in the paper they assumed
$\mathfrak {t=c}$
implies that there is a Katětov maximal MAD family. We will now improve this result. Our method is a refinement of theirs. Although in the paper they assumed
![]() $\mathfrak {t=c},$
it is not hard to see that their arguments can be carried out under
$\mathfrak {t=c},$
it is not hard to see that their arguments can be carried out under
![]() $\mathfrak {h=c}$
. The Katětov maximal MAD family is constructed recursively. At any given step of the recursion, there are less than
$\mathfrak {h=c}$
. The Katětov maximal MAD family is constructed recursively. At any given step of the recursion, there are less than
![]() $\mathfrak {c}$
many open dense subsets of
$\mathfrak {c}$
many open dense subsets of
![]() $\left [ \omega \right ] ^{\omega }$
that need to be intersected in order to proceed. This is the reason that
$\left [ \omega \right ] ^{\omega }$
that need to be intersected in order to proceed. This is the reason that
![]() $\mathfrak {h=c}$
is enough to carry out the construction. It turns out that by being even more careful, it is possible to prove that
$\mathfrak {h=c}$
is enough to carry out the construction. It turns out that by being even more careful, it is possible to prove that
![]() $\mathfrak {b=c}$
is enough to intersect all the open dense sets that are needed in the recursion.
$\mathfrak {b=c}$
is enough to intersect all the open dense sets that are needed in the recursion.
If we want to recursively construct a Katětov maximal MAD family, we immediately run into a conceptual problem. A MAD family needs to be constructed in (at most)
![]() $\mathfrak {c}$
steps, while there are
$\mathfrak {c}$
steps, while there are
![]() $2^{\mathfrak {c}}$
MAD families to take care of. There are much more requirements than steps of the recursion. García-Ferreira and Hrušák found a very clever to way to circumvent the problem. First we need the following notion:
$2^{\mathfrak {c}}$
MAD families to take care of. There are much more requirements than steps of the recursion. García-Ferreira and Hrušák found a very clever to way to circumvent the problem. First we need the following notion:
Definition 29. Let
![]() $\mathcal {A}$
be a MAD family. We say that
$\mathcal {A}$
be a MAD family. We say that
![]() $\mathcal {A}$
is Katětov uniform if
$\mathcal {A}$
is Katětov uniform if
![]() $\mathcal {A}$
is Katětov equivalent to all of its restrictions.
$\mathcal {A}$
is Katětov equivalent to all of its restrictions.
Equivalently,
![]() $\mathcal {A}$
is Katětov uniform if and only if
$\mathcal {A}$
is Katětov uniform if and only if
![]() $\mathcal {A}\upharpoonright X\leq _{\textsf {K}}\mathcal {A}$
for every
$\mathcal {A}\upharpoonright X\leq _{\textsf {K}}\mathcal {A}$
for every
![]() ${X\in \mathcal {I(A)}^{+}.}$
Every Katětov maximal MAD family is Katětov uniform. In [Reference Hrušák and Ferreira40] it was proved the following:
${X\in \mathcal {I(A)}^{+}.}$
Every Katětov maximal MAD family is Katětov uniform. In [Reference Hrušák and Ferreira40] it was proved the following:
Proposition 30 [Reference Hrušák and Ferreira40].
Let
![]() $\mathcal {A}$
be a MAD family. If
$\mathcal {A}$
be a MAD family. If
![]() $\mathcal {A}$
is Katětov uniform and weakly tight, then
$\mathcal {A}$
is Katětov uniform and weakly tight, then
![]() $\mathcal {A}$
is Katětov maximal.
$\mathcal {A}$
is Katětov maximal.
The great advantage of the Proposition is that in principle, constructing a weakly tight, Katětov uniform MAD family requires only
![]() $\mathfrak {c}$
many steps. In this way, if we want to build a Katětov maximal MAD family, it is enough to build a weakly tight, Katětov uniform MAD family. Thus we reduce the number of tasks needed from
$\mathfrak {c}$
many steps. In this way, if we want to build a Katětov maximal MAD family, it is enough to build a weakly tight, Katětov uniform MAD family. Thus we reduce the number of tasks needed from
![]() $2^{\mathfrak {c}}$
to
$2^{\mathfrak {c}}$
to
![]() $\mathfrak {c}.$
The drawback is that the MAD families constructed in this way are necessarily also weakly tight. It is currently unknown if Katětov maximality implies weak tightness (however, in the next section we show that it does not imply tightness).
$\mathfrak {c}.$
The drawback is that the MAD families constructed in this way are necessarily also weakly tight. It is currently unknown if Katětov maximality implies weak tightness (however, in the next section we show that it does not imply tightness).
In [Reference Hrušák and Ferreira40] a Katětov uniform MAD family was constructed assuming
![]() $\mathfrak {t=c}$
. The method used in there was not sufficient to build a maximal one. This was achieved until [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1] where a novel idea was employed: along the construction of the Katětov maximal MAD family, a partial cofinitary semigroup was also constructed. Partial cofinitary semigroups are related to the more well studied cofinitary groups. Maximal cofinitary groups have been deeply studied in Set Theory. The reader wishing to know more about this topic, may consult [Reference Brendle, Spinas and Zhang10, Reference Fischer, Schrittesser and Törnquist23, Reference Fischer and Törnquist22, Reference Gao and Zhang26, Reference Hrušák, Steprans and Zhang45, Reference Kastermans47, Reference Kastermans48].
$\mathfrak {t=c}$
. The method used in there was not sufficient to build a maximal one. This was achieved until [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1] where a novel idea was employed: along the construction of the Katětov maximal MAD family, a partial cofinitary semigroup was also constructed. Partial cofinitary semigroups are related to the more well studied cofinitary groups. Maximal cofinitary groups have been deeply studied in Set Theory. The reader wishing to know more about this topic, may consult [Reference Brendle, Spinas and Zhang10, Reference Fischer, Schrittesser and Törnquist23, Reference Fischer and Törnquist22, Reference Gao and Zhang26, Reference Hrušák, Steprans and Zhang45, Reference Kastermans47, Reference Kastermans48].
We will denote by
![]() $Id$
the identity function on
$Id$
the identity function on
![]() $\omega .$
We will now clarify what we mean by the composition of two partial functions from
$\omega .$
We will now clarify what we mean by the composition of two partial functions from
![]() $\omega $
to
$\omega $
to
![]() $\omega .$
$\omega .$
Definition 31. Let
![]() $f:A\longrightarrow \omega $
and
$f:A\longrightarrow \omega $
and
![]() $g:B\longrightarrow \omega $
where
$g:B\longrightarrow \omega $
where
![]() $A,B\subseteq \omega .$
The composition
$A,B\subseteq \omega .$
The composition
![]() $gf:C\longrightarrow \omega $
is defined as follows
$gf:C\longrightarrow \omega $
is defined as follows
![]() $:$
$:$
-
1.
 $C=\left \{ a\in A\mid f\left ( a\right ) \in B\right \} .$
$C=\left \{ a\in A\mid f\left ( a\right ) \in B\right \} .$
-
2. Let
 $a\in C.$
Define
$a\in C.$
Define
 $gf\left ( a\right ) =x$
if
$gf\left ( a\right ) =x$
if
 $g\left ( f\left ( a\right ) \right ) =x.$
$g\left ( f\left ( a\right ) \right ) =x.$
In other words,
![]() $gf=\left \{ \left ( a,x\right ) \mid a\in A\wedge \exists b\in B\left ( \left ( a,b\right ) \in f\wedge \left ( b,x\right ) \in g\right ) \right \} $
(see [Reference Enderton19]). If
$gf=\left \{ \left ( a,x\right ) \mid a\in A\wedge \exists b\in B\left ( \left ( a,b\right ) \in f\wedge \left ( b,x\right ) \in g\right ) \right \} $
(see [Reference Enderton19]). If
![]() $f\in \omega ^{\omega }$
is an injective function, by
$f\in \omega ^{\omega }$
is an injective function, by
![]() $f^{-1}$
we denote the function with domain img
$f^{-1}$
we denote the function with domain img
![]() $\left ( f\right ) $
and such that
$\left ( f\right ) $
and such that
![]() $f^{-1}f\left ( n\right ) =n$
for every
$f^{-1}f\left ( n\right ) =n$
for every
![]() $n\in \omega .$
The following lemma is a particular case of Theorem 3G of [Reference Enderton19].
$n\in \omega .$
The following lemma is a particular case of Theorem 3G of [Reference Enderton19].
Lemma 32. Let
![]() $f:\omega \longrightarrow \omega $
be an injective function and
$f:\omega \longrightarrow \omega $
be an injective function and
![]() $A\subseteq \omega .$
$A\subseteq \omega .$
-
1.
 $f^{-1}f$
is the identity function on
$f^{-1}f$
is the identity function on
 $\omega .$
$\omega .$
-
2.
 $\,ff^{-1}$
is the identity function on img
$\,ff^{-1}$
is the identity function on img
 $\left ( f\right ) .$
$\left ( f\right ) .$
-
3.
 $f^{-1}f\left [ A\right ] =A$
and
$f^{-1}f\left [ A\right ] =A$
and
 $ff^{-1}\left [ A\right ] \subseteq A$
(but might be smaller).
$ff^{-1}\left [ A\right ] \subseteq A$
(but might be smaller).
It is worth emphasizing that in general, the functions we will be using will be injections but not surjections on
![]() $\omega .$
We need to be very careful when canceling. The reason we explicitly wrote the previous lemma is to remind the reader which cancellations are valid and which ones are not.
$\omega .$
We need to be very careful when canceling. The reason we explicitly wrote the previous lemma is to remind the reader which cancellations are valid and which ones are not.
Definition 33. Let
![]() $S\subseteq \omega ^{\omega }$
be a family of injective functions. We say that a partial function
$S\subseteq \omega ^{\omega }$
be a family of injective functions. We say that a partial function
![]() $w;\omega \longrightarrow \omega $
is a (reduced) word on S if there are
$w;\omega \longrightarrow \omega $
is a (reduced) word on S if there are
![]() $f_{1},\dots ,f_{n}\in S$
and
$f_{1},\dots ,f_{n}\in S$
and
![]() $r_{1},\dots ,r_{n} \in \mathbb {Z}$
such that
$r_{1},\dots ,r_{n} \in \mathbb {Z}$
such that
![]() $:$
$:$
-
1.
 $r_{i}\neq 0$
for all
$r_{i}\neq 0$
for all
 $i\leq n.$
$i\leq n.$
-
2.
 $w=f_{1}^{r_{1}}f_{2}^{r_{2}}\dots f_{n}^{r_{n}}.$
$w=f_{1}^{r_{1}}f_{2}^{r_{2}}\dots f_{n}^{r_{n}}.$
-
3.
 $f_{i+1}\notin \left \{ f_{i},f_{i}^{-1}\right \} $
and
$f_{i+1}\notin \left \{ f_{i},f_{i}^{-1}\right \} $
and
 $f_{i} \notin \left \{ f_{i+1},f_{i+1}^{-1}\right \} $
for all
$f_{i} \notin \left \{ f_{i+1},f_{i+1}^{-1}\right \} $
for all
 $i<n.$
$i<n.$
We would like to point out that for us, a word is an actual partial function. Not a symbolic representation of it. It is easy to see that if w is a word, then
![]() $w^{-1}$
is also a word. Note that if
$w^{-1}$
is also a word. Note that if
![]() $f\in S,$
then dom
$f\in S,$
then dom
![]() $\left ( f\right ) =\omega ,$
but the domain of
$\left ( f\right ) =\omega ,$
but the domain of
![]() $f^{-1}$
might be a proper subset of
$f^{-1}$
might be a proper subset of
![]() $\omega .$
$\omega .$
By
![]() $\mathbb {W}\left ( S\right ) $
we denote the set of all reduced words on
$\mathbb {W}\left ( S\right ) $
we denote the set of all reduced words on
![]() $S.$
It is clear that if
$S.$
It is clear that if
![]() $w\in \mathbb {W}\left ( S\right ) ,$
then w is an injective partial function and
$w\in \mathbb {W}\left ( S\right ) ,$
then w is an injective partial function and
![]() $w^{-1}$
is also in
$w^{-1}$
is also in
![]() $\mathbb {W}\left ( S\right ) .$
It is easy to see that
$\mathbb {W}\left ( S\right ) .$
It is easy to see that
![]() $\left \vert \mathbb {W}\left ( S\right ) \right \vert \leq \left \vert S\right \vert +\omega .$
Given
$\left \vert \mathbb {W}\left ( S\right ) \right \vert \leq \left \vert S\right \vert +\omega .$
Given
![]() $w\in \mathbb {W}\left ( S\right ) $
,
$w\in \mathbb {W}\left ( S\right ) $
,
![]() $f_{1},\dots ,f_{n}\in S$
and
$f_{1},\dots ,f_{n}\in S$
and
![]() $r_{1},\dots ,r_{n}\in \mathbb {Z}$
as above, we will implicitly assume that if
$r_{1},\dots ,r_{n}\in \mathbb {Z}$
as above, we will implicitly assume that if
![]() $n\neq 1,$
then each
$n\neq 1,$
then each
![]() $f_{i}\neq Id,$
and ff
$f_{i}\neq Id,$
and ff
![]() $n=1$
and
$n=1$
and
![]() $f_{1}=Id,$
then
$f_{1}=Id,$
then
![]() $r_{1}=1.$
Every word has a length, which is computed in the following way: let
$r_{1}=1.$
Every word has a length, which is computed in the following way: let
![]() $w\in \mathbb {W}\left ( S\right ) ,$
the length of w is smallest number of the form
$w\in \mathbb {W}\left ( S\right ) ,$
the length of w is smallest number of the form
![]() $\underset {i\leq n}{\sum }|r_{i}|$
where
$\underset {i\leq n}{\sum }|r_{i}|$
where
![]() $w=f_{1}^{r_{1}}f_{2}^{r_{2}}\dots f_{n}^{r_{n}}$
are as above.
$w=f_{1}^{r_{1}}f_{2}^{r_{2}}\dots f_{n}^{r_{n}}$
are as above.
Lemma 34. Let
![]() $S\subseteq \omega ^{\omega }$
be a family of injective functions and
$S\subseteq \omega ^{\omega }$
be a family of injective functions and
![]() $p,q,w\in \mathbb {W}\left ( S\right ) .$
If
$p,q,w\in \mathbb {W}\left ( S\right ) .$
If
![]() $A\subseteq \omega ,$
then
$A\subseteq \omega ,$
then
![]() $pww^{-1}q\left [ A\right ] \subseteq pq\left [ A\right ] .$
$pww^{-1}q\left [ A\right ] \subseteq pq\left [ A\right ] .$
We now introduce the following notion, which will play a key role in the rest of the paper:
Definition 35. Let
![]() $S\subseteq \omega ^{\omega }.$
We say that S is a partial cofinitary semigroup base if the following conditions hold
$S\subseteq \omega ^{\omega }.$
We say that S is a partial cofinitary semigroup base if the following conditions hold
![]() $:$
$:$
-
1. S is a family of injective functions.
-
2.
 $Id\in S.$
$Id\in S.$
-
3.
 $\mathbb {W}\left ( S\right ) $
is an AD family (we view every partial function as a subset of
$\mathbb {W}\left ( S\right ) $
is an AD family (we view every partial function as a subset of
 $\omega \times \omega $
).
$\omega \times \omega $
).
We would like to point out that
![]() $\mathbb {W}\left ( S\right ) $
may not be a semigroup. This is because while
$\mathbb {W}\left ( S\right ) $
may not be a semigroup. This is because while
![]() $\mathbb {W}\left ( S\right ) $
is closed under many compositions, it may not closed under all of them (for example, if
$\mathbb {W}\left ( S\right ) $
is closed under many compositions, it may not closed under all of them (for example, if
![]() $f\in S,$
then
$f\in S,$
then
![]() $ff^{-1}$
may not be in
$ff^{-1}$
may not be in
![]() $\mathbb {W}\left ( S\right ) $
).
$\mathbb {W}\left ( S\right ) $
).
Given a partial function
![]() $f,$
define Fix
$f,$
define Fix
![]() $\left ( f\right ) =\{n\in $
dom
$\left ( f\right ) =\{n\in $
dom
![]() $\left ( f\right ) \mid f\left ( n\right ) =n\}.$
We now have the following:
$\left ( f\right ) \mid f\left ( n\right ) =n\}.$
We now have the following:
Lemma 36. Let S be a partial cofinitary semigroup base and
![]() $w\in \mathbb {W}\left ( S\right ) .$
If
$w\in \mathbb {W}\left ( S\right ) .$
If
![]() $w\neq Id,$
then Fix
$w\neq Id,$
then Fix
![]() $\left ( w\right ) $
is finite.
$\left ( w\right ) $
is finite.
Proof The lemma follows because
![]() $Id\in S,$
so w and
$Id\in S,$
so w and
![]() $Id$
are almost disjoint.
$Id$
are almost disjoint.
An important feature of partial cofinitary semigroup bases is the following:
Lemma 37. Let S be a partial cofinitary semigroup base,
![]() $w,z\in \mathbb {W}\left ( S\right ) $
with
$w,z\in \mathbb {W}\left ( S\right ) $
with
![]() $w\neq z$
and
$w\neq z$
and
![]() $X\in \left [ \omega \right ] ^{\omega }.$
There is
$X\in \left [ \omega \right ] ^{\omega }.$
There is
![]() $Y\in \left [ X\right ] ^{\omega }$
such that
$Y\in \left [ X\right ] ^{\omega }$
such that
![]() $w\left [ Y\right ] \cap z\left [ Y\right ] =\emptyset .$
$w\left [ Y\right ] \cap z\left [ Y\right ] =\emptyset .$
Proof We will recursively define
![]() $Y=\left \{ y_{n}\mid n\in \omega \right \} \subseteq X$
as follows: First, we choose
$Y=\left \{ y_{n}\mid n\in \omega \right \} \subseteq X$
as follows: First, we choose
![]() $y_{0}\in X$
such that either
$y_{0}\in X$
such that either
![]() $y_{0}\notin $
dom
$y_{0}\notin $
dom
![]() $\left ( w\right ) \cap $
dom
$\left ( w\right ) \cap $
dom
![]() $\left ( z\right ) $
or
$\left ( z\right ) $
or
![]() $w\left ( y_{0}\right ) \neq z\left ( y_{0}\right ) $
(recall that w and z are almost disjoint). Assume we have defined
$w\left ( y_{0}\right ) \neq z\left ( y_{0}\right ) $
(recall that w and z are almost disjoint). Assume we have defined
![]() $y_{0},\dots ,y_{n},$
we will now define
$y_{0},\dots ,y_{n},$
we will now define
![]() $y_{n+1}.$
Let
$y_{n+1}.$
Let
![]() $t_{n+1}=\left \{ y_{0},\dots ,y_{n}\right \} .$
We now choose
$t_{n+1}=\left \{ y_{0},\dots ,y_{n}\right \} .$
We now choose
![]() $y_{n+1}\in X$
with the following properties:
$y_{n+1}\in X$
with the following properties:
-
1.
 $y_{n+1}\notin t_{n+1}\cup z^{-1}\left ( w\left [ t_{n+1}\right ] \right ) \cup w^{-1}\left ( z\left [ t_{n+1}\right ] \right ) .$
$y_{n+1}\notin t_{n+1}\cup z^{-1}\left ( w\left [ t_{n+1}\right ] \right ) \cup w^{-1}\left ( z\left [ t_{n+1}\right ] \right ) .$
-
2. Either
 $y_{n+1}\notin $
dom
$y_{n+1}\notin $
dom
 $\left ( w\right ) \cap $
dom
$\left ( w\right ) \cap $
dom
 $\left ( z\right ) $
or
$\left ( z\right ) $
or
 $\ w\left ( y_{n+1}\right ) \neq z\left ( y_{n+1}\right ) .$
$\ w\left ( y_{n+1}\right ) \neq z\left ( y_{n+1}\right ) .$
This is easy to do since both w and z are injective and they are almost disjoint. We claim that
![]() $Y=\left \{ y_{n}\mid n\in \omega \right \} $
is as desired. Assume this is not the case, so there are
$Y=\left \{ y_{n}\mid n\in \omega \right \} $
is as desired. Assume this is not the case, so there are
![]() $i,j\in \omega $
such that
$i,j\in \omega $
such that
![]() $w\left ( y_{i}\right ) =z\left ( y_{j}\right ) .$
By construction, it is impossible that
$w\left ( y_{i}\right ) =z\left ( y_{j}\right ) .$
By construction, it is impossible that
![]() $i=j.$
Assume that
$i=j.$
Assume that
![]() $i<j$
(the other case is symmetrical). We get that
$i<j$
(the other case is symmetrical). We get that
![]() $y_{j}\in z^{-1}\left ( w\left [ t_{j}\right ] \right ) ,$
but this is impossible.
$y_{j}\in z^{-1}\left ( w\left [ t_{j}\right ] \right ) ,$
but this is impossible.
We will now recall the following definitions:
Definition 38.
-
1. Let
 $h:\omega ^{<\omega \nearrow }\longrightarrow \omega .$
A function
$h:\omega ^{<\omega \nearrow }\longrightarrow \omega .$
A function
 $\pi :\omega ^{<\omega \nearrow }\longrightarrow \left [ \omega \right ] ^{<\omega }$
is an h-slalom predictor if
$\pi :\omega ^{<\omega \nearrow }\longrightarrow \left [ \omega \right ] ^{<\omega }$
is an h-slalom predictor if
 $\left \vert \pi \left ( s\right ) \right \vert \leq h\left ( s\right ) $
for every
$\left \vert \pi \left ( s\right ) \right \vert \leq h\left ( s\right ) $
for every
 $s\in \omega ^{<\omega \nearrow }.$
$s\in \omega ^{<\omega \nearrow }.$
-
2. Let
 $\pi :\omega ^{<\omega \nearrow }\longrightarrow \left [ \omega \right ] ^{<\omega }$
and
$\pi :\omega ^{<\omega \nearrow }\longrightarrow \left [ \omega \right ] ^{<\omega }$
and
 $g\in \omega ^{\omega }$
an increasing function. We say that g escapes from
$g\in \omega ^{\omega }$
an increasing function. We say that g escapes from
 $\pi $
if there are only finitely many
$\pi $
if there are only finitely many
 $n\in \omega $
for which
$n\in \omega $
for which
 $g\left ( n\right ) \in \pi (g\upharpoonright n)$
.
$g\left ( n\right ) \in \pi (g\upharpoonright n)$
.
In [Reference Brendle and Yatabe10], Brendle, Spinas, and Zhang proved the following very useful theorem:
Theorem 39 [Reference Brendle and Yatabe10].
Let
![]() $\kappa $
be an infinite cardinal. The following are equivalent
$\kappa $
be an infinite cardinal. The following are equivalent
![]() $:$
$:$
-
1.
 $\kappa <$
non
$\kappa <$
non
 $\left ( \mathcal {M}\right ) .$
$\left ( \mathcal {M}\right ) .$
-
2. For every
 $h:\omega ^{<\omega \nearrow }\longrightarrow \omega $
and
$h:\omega ^{<\omega \nearrow }\longrightarrow \omega $
and
 $\left \{ \pi _{\alpha }\mid \alpha <\kappa \right \} $
a set of h-slalom predictors, there is
$\left \{ \pi _{\alpha }\mid \alpha <\kappa \right \} $
a set of h-slalom predictors, there is
 $g\in \omega ^{\omega }$
an increasing function that escapes from each of the
$g\in \omega ^{\omega }$
an increasing function that escapes from each of the
 $\pi _{\alpha }.$
$\pi _{\alpha }.$
With this theorem, we can prove the following:
Proposition 40. Let S be a partial cofinitary semigroup base with
![]() $\left \vert S\right \vert <$
non
$\left \vert S\right \vert <$
non
![]() $\left ( \mathcal {M}\right ) $
and
$\left ( \mathcal {M}\right ) $
and
![]() $X\in \left [ \omega \right ] ^{\omega }.$
There is
$X\in \left [ \omega \right ] ^{\omega }.$
There is
![]() $Y\in \left [ X\right ] ^{\omega }$
such that for all
$Y\in \left [ X\right ] ^{\omega }$
such that for all
![]() $w,z\in \mathbb {W}\left ( S\right ) ,$
if
$w,z\in \mathbb {W}\left ( S\right ) ,$
if
![]() $w\neq z,$
then
$w\neq z,$
then
![]() $w\left [ Y\right ] \cap z\left [ Y\right ] $
is finite.Footnote
4
$w\left [ Y\right ] \cap z\left [ Y\right ] $
is finite.Footnote
4
Proof Let
![]() $l:\omega \longrightarrow X$
be its enumerating function and
$l:\omega \longrightarrow X$
be its enumerating function and
![]() $\mathbb {W} \left ( S\right ) =\left \{ w_{\alpha }\mid \alpha <\kappa \right \} $
(for some cardinal
$\mathbb {W} \left ( S\right ) =\left \{ w_{\alpha }\mid \alpha <\kappa \right \} $
(for some cardinal
![]() $\kappa $
that is smaller than non
$\kappa $
that is smaller than non
![]() $\left ( \mathcal {M} \right ) $
). Given
$\left ( \mathcal {M} \right ) $
). Given
![]() $\alpha ,\beta <\kappa $
with
$\alpha ,\beta <\kappa $
with
![]() $\alpha \neq \beta ,$
we define the slalom predictor:
$\alpha \neq \beta ,$
we define the slalom predictor:
![]() $\begin {array} [c]{c} \pi _{\alpha \beta }:\omega ^{<\omega \nearrow }\longrightarrow \left [ \omega \right ] ^{<\omega }. \end {array} $
$\begin {array} [c]{c} \pi _{\alpha \beta }:\omega ^{<\omega \nearrow }\longrightarrow \left [ \omega \right ] ^{<\omega }. \end {array} $
Given as follows:
-
1.
 $\pi _{\alpha \beta }\left ( \emptyset \right ) =\emptyset .$
$\pi _{\alpha \beta }\left ( \emptyset \right ) =\emptyset .$
-
2. Let
 $t\in \omega ^{<\omega \nearrow }$
with
$t\in \omega ^{<\omega \nearrow }$
with
 $t\neq \emptyset .$
Define:
$t\neq \emptyset .$
Define:
 $\begin {array} [c]{cccc} \pi _{\alpha \beta }\left ( t\right ) & = & \textsf {img}\left ( t\right ) & \cup \\ & & l^{-1}(w_{\alpha }^{-1}(w_{\beta }[l[{\textsf {img}}\left ( t\right ) ]])) & \cup \\ & & l^{-1}(w_{\beta }^{-1}(w_{\alpha }[l[{\textsf {img}}\left ( t\right ) ]])). & \end {array} $
$\begin {array} [c]{cccc} \pi _{\alpha \beta }\left ( t\right ) & = & \textsf {img}\left ( t\right ) & \cup \\ & & l^{-1}(w_{\alpha }^{-1}(w_{\beta }[l[{\textsf {img}}\left ( t\right ) ]])) & \cup \\ & & l^{-1}(w_{\beta }^{-1}(w_{\alpha }[l[{\textsf {img}}\left ( t\right ) ]])). & \end {array} $
It is easy to see that there is a function
![]() $h:\omega ^{<\omega \nearrow }\longrightarrow \omega $
such that each
$h:\omega ^{<\omega \nearrow }\longrightarrow \omega $
such that each
![]() $\pi _{\alpha \beta }$
is an h-slalom predictor. Since
$\pi _{\alpha \beta }$
is an h-slalom predictor. Since
![]() $\kappa $
is smaller than non
$\kappa $
is smaller than non
![]() $\left ( \mathcal {M} \right ) ,$
by Theorem 39, we know there is an increasing function
$\left ( \mathcal {M} \right ) ,$
by Theorem 39, we know there is an increasing function
![]() $g\in \omega ^{\omega }$
that escapes from each
$g\in \omega ^{\omega }$
that escapes from each
![]() $\pi _{\alpha \beta }.$
Define
$\pi _{\alpha \beta }.$
Define
![]() $Y=\left \{ l\left ( g\left ( n\right ) \right ) \mid n\in \omega \right \} .$
Since g is injective, it follows that Y is an infinite subset of
$Y=\left \{ l\left ( g\left ( n\right ) \right ) \mid n\in \omega \right \} .$
Since g is injective, it follows that Y is an infinite subset of
![]() $X.$
We will show that Y has the desired property. Let
$X.$
We will show that Y has the desired property. Let
![]() $\alpha ,\beta <\kappa $
with
$\alpha ,\beta <\kappa $
with
![]() $\alpha \neq \beta ,$
we need to prove that
$\alpha \neq \beta ,$
we need to prove that
![]() $w_{\alpha }\left [ Y\right ] \cap w_{\beta }\left [ Y\right ] $
is finite. In order to achieve this, it is enough to prove that the set
$w_{\alpha }\left [ Y\right ] \cap w_{\beta }\left [ Y\right ] $
is finite. In order to achieve this, it is enough to prove that the set
![]() $P=\left \{ \left ( i,j\right ) \mid w_{\alpha }\left ( lg\left ( i\right ) \right ) =w_{\beta }\left ( lg\left ( j\right ) \right ) \right \} $
is finite. Let
$P=\left \{ \left ( i,j\right ) \mid w_{\alpha }\left ( lg\left ( i\right ) \right ) =w_{\beta }\left ( lg\left ( j\right ) \right ) \right \} $
is finite. Let
![]() $\left ( i,j\right ) \in P.$
$\left ( i,j\right ) \in P.$
First, consider the case where
![]() $i\neq j.$
Without lost of generality, we may assume that
$i\neq j.$
Without lost of generality, we may assume that
![]() $i<j.$
Let
$i<j.$
Let
![]() $t=g\upharpoonright j$
(so img
$t=g\upharpoonright j$
(so img
![]() $\left ( t\right ) =g\left [ j\right ] $
). Clearly
$\left ( t\right ) =g\left [ j\right ] $
). Clearly
![]() $w_{\alpha }\left ( lg\left ( i\right ) \right ) \in w_{\alpha }\left [ lg\left [ j\right ] \right ] ,$
so
$w_{\alpha }\left ( lg\left ( i\right ) \right ) \in w_{\alpha }\left [ lg\left [ j\right ] \right ] ,$
so
![]() $w_{\beta }\left ( lg\left ( j\right ) \right ) \in w_{\alpha }\left [ lg\left [ j\right ] \right ] .$
In this way,
$w_{\beta }\left ( lg\left ( j\right ) \right ) \in w_{\alpha }\left [ lg\left [ j\right ] \right ] .$
In this way,
![]() $lg\left ( j\right ) \in w_{\beta } ^{-1}\left ( w_{\alpha }\left [ lg\left [ j\right ] \right ] \right ) $
and then,
$lg\left ( j\right ) \in w_{\beta } ^{-1}\left ( w_{\alpha }\left [ lg\left [ j\right ] \right ] \right ) $
and then,
![]() $g\left ( j\right ) \in l^{-1}\left ( w_{\beta }^{-1}\left ( w_{\alpha }\left [ lg\left [ j\right ] \right ] \right ) \right ) \subseteq \pi _{\alpha \beta }\left ( g\upharpoonright j\right ) .$
Since g escapes from
$g\left ( j\right ) \in l^{-1}\left ( w_{\beta }^{-1}\left ( w_{\alpha }\left [ lg\left [ j\right ] \right ] \right ) \right ) \subseteq \pi _{\alpha \beta }\left ( g\upharpoonright j\right ) .$
Since g escapes from
![]() $\pi _{\alpha \beta },$
there can only be finitely many
$\pi _{\alpha \beta },$
there can only be finitely many
![]() $\left ( i,j\right ) $
in which this case holds.
$\left ( i,j\right ) $
in which this case holds.
In case
![]() $i=j,$
we would have that
$i=j,$
we would have that
![]() $w_{\alpha }\left ( lg\left ( i\right ) \right ) =w_{\beta }\left ( lg\left ( i\right ) \right ) .$
Since
$w_{\alpha }\left ( lg\left ( i\right ) \right ) =w_{\beta }\left ( lg\left ( i\right ) \right ) .$
Since
![]() $w_{\alpha }$
and
$w_{\alpha }$
and
![]() $w_{\beta }$
are almost disjoint, there are only finitely many pairs
$w_{\beta }$
are almost disjoint, there are only finitely many pairs
![]() $\left ( i,j\right ) $
that fall in this case. This finishes the proof.
$\left ( i,j\right ) $
that fall in this case. This finishes the proof.
Recall that if S is a partial cofinitary semigroup base, then the identity mapping is in
![]() $S.$
In this way, under the hypothesis of the proposition above, if
$S.$
In this way, under the hypothesis of the proposition above, if
![]() $w\in \mathbb {W}\left ( S\right ) $
and is not the identity, then
$w\in \mathbb {W}\left ( S\right ) $
and is not the identity, then
![]() $w\left [ Y\right ] \cap Y$
is finite. This fact will be used several times implicitly.
$w\left [ Y\right ] \cap Y$
is finite. This fact will be used several times implicitly.
Definition 41. Let
![]() $S\subseteq \omega ^{\omega }$
be a partial cofinitary semigroup base and
$S\subseteq \omega ^{\omega }$
be a partial cofinitary semigroup base and
![]() $\mathcal {A}$
an AD family. We say that S respects
$\mathcal {A}$
an AD family. We say that S respects
![]() $\mathcal {A}$
if for every
$\mathcal {A}$
if for every
![]() $w\in \mathbb {W}\left ( S\right ) $
and
$w\in \mathbb {W}\left ( S\right ) $
and
![]() $A\in \mathcal {A},$
we have that
$A\in \mathcal {A},$
we have that
![]() $w\left [ A\right ] \in \mathcal {A}\cup \left [ \omega \right ] ^{<\omega }.$
$w\left [ A\right ] \in \mathcal {A}\cup \left [ \omega \right ] ^{<\omega }.$
We get the following:
Lemma 42. Let
![]() $S\subseteq \omega ^{\omega }$
be a partial cofinitary semigroup base and
$S\subseteq \omega ^{\omega }$
be a partial cofinitary semigroup base and
![]() $\mathcal {A}$
an AD family such that S respects
$\mathcal {A}$
an AD family such that S respects
![]() $\mathcal {A}.$
If
$\mathcal {A}.$
If
![]() $X\in \mathcal {A}^{\perp }$
and
$X\in \mathcal {A}^{\perp }$
and
![]() $w\in \mathbb {W}\left ( S\right ) ,$
then
$w\in \mathbb {W}\left ( S\right ) ,$
then
![]() $w\left [ X\right ] \in \mathcal {A}^{\perp }.$
$w\left [ X\right ] \in \mathcal {A}^{\perp }.$
Proof We argue by contradiction. Assume that there is
![]() $A\in \mathcal {A}$
such that
$A\in \mathcal {A}$
such that
![]() ${A\cap w\left [ X\right ] }$
is infinite. This implies that
${A\cap w\left [ X\right ] }$
is infinite. This implies that
![]() $w^{-1}\left ( A\right ) \cap X$
is infinite, but this is a contradiction since
$w^{-1}\left ( A\right ) \cap X$
is infinite, but this is a contradiction since
![]() $w^{-1}\left ( A\right ) \in \mathcal {A}\cup \left [ \omega \right ] ^{<\omega }.$
$w^{-1}\left ( A\right ) \in \mathcal {A}\cup \left [ \omega \right ] ^{<\omega }.$
We will use the following theorem of [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1], which is a generalization of a theorem in [Reference Brendle and Yatabe10]:
Proposition 43 [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1].
Let S be a partial cofinitary semigroup base with
![]() $\left \vert S\right \vert <$
non
$\left \vert S\right \vert <$
non
![]() $\left ( \mathcal {M}\right ) .$
For every
$\left ( \mathcal {M}\right ) .$
For every
![]() $Y\in \left [ \omega \right ] ^{\omega },$
there is an injective function
$Y\in \left [ \omega \right ] ^{\omega },$
there is an injective function
![]() $f:\omega \longrightarrow Y$
such that
$f:\omega \longrightarrow Y$
such that
![]() $S\cup \left \{ f\right \} $
is a partial cofinitary semigroup base.
$S\cup \left \{ f\right \} $
is a partial cofinitary semigroup base.
We now introduce the following notion:
Definition 44. We say that
![]() $(S,\mathcal {A})$
is a nice pair if the following conditions hold
$(S,\mathcal {A})$
is a nice pair if the following conditions hold
![]() $:$
$:$
-
1. S is a partial cofinitary semigroup base.
-
2.
 $\mathcal {A}\neq \emptyset $
is an AD family.
$\mathcal {A}\neq \emptyset $
is an AD family. -
3.
 $\mathcal {L(}S,\mathcal {A)}=\{w\left [ A\right ] \mid w\in \mathbb {W}\left ( S\right ) \wedge A\in \mathcal {A}\}\setminus \lbrack \omega ]^{<\omega }$
is an AD family.
$\mathcal {L(}S,\mathcal {A)}=\{w\left [ A\right ] \mid w\in \mathbb {W}\left ( S\right ) \wedge A\in \mathcal {A}\}\setminus \lbrack \omega ]^{<\omega }$
is an AD family.
Note that if
![]() $(S,\mathcal {A})$
is a nice pair, it might not be the case that S respects
$(S,\mathcal {A})$
is a nice pair, it might not be the case that S respects
![]() $\mathcal {L(}S,\mathcal {A)}.$
For example, take
$\mathcal {L(}S,\mathcal {A)}.$
For example, take
![]() $A\in \mathcal {A}$
and
$A\in \mathcal {A}$
and
![]() $f\in S.$
Clearly
$f\in S.$
Clearly
![]() $f^{-1}\left [ A\right ] \in \mathcal {L(}S,\mathcal {A)},$
but
$f^{-1}\left [ A\right ] \in \mathcal {L(}S,\mathcal {A)},$
but
![]() $ff^{-1}\left [ A\right ] $
might be a proper subset of
$ff^{-1}\left [ A\right ] $
might be a proper subset of
![]() $A.$
Nevertheless, we can get a similar conclusion to the one of Lemma 42:
$A.$
Nevertheless, we can get a similar conclusion to the one of Lemma 42:
Lemma 45. Let
![]() $(S,\mathcal {A})$
be a nice pair and
$(S,\mathcal {A})$
be a nice pair and
![]() $Y\in \mathcal {L(}S,\mathcal {A)} ^{\perp }.$
If
$Y\in \mathcal {L(}S,\mathcal {A)} ^{\perp }.$
If
![]() $w\in \mathbb {W}\left ( S\right ) ,$
then
$w\in \mathbb {W}\left ( S\right ) ,$
then
![]() $w\left [ Y\right ] \in \mathcal {L(}S,\mathcal {A)}^{\perp }.$
$w\left [ Y\right ] \in \mathcal {L(}S,\mathcal {A)}^{\perp }.$
Proof We will first prove that
![]() $w\left [ Y\right ] \in \mathcal {A}^{\perp }.$
If this was not the case, then there is
$w\left [ Y\right ] \in \mathcal {A}^{\perp }.$
If this was not the case, then there is
![]() $A\in \mathcal {A}$
such that
$A\in \mathcal {A}$
such that
![]() $A\cap w\left [ Y\right ] $
is infinite. But this implies that
$A\cap w\left [ Y\right ] $
is infinite. But this implies that
![]() $w^{-1}\left [ A\right ] \cap Y$
is infinite, which is a contradiction.
$w^{-1}\left [ A\right ] \cap Y$
is infinite, which is a contradiction.
We now prove the general case. Once again, we proceed by contradiction. Assume this is not the case, so there is
![]() $z\in \mathbb {W}\left ( S\right ) $
and
$z\in \mathbb {W}\left ( S\right ) $
and
![]() $A\in \mathcal {A}$
such that
$A\in \mathcal {A}$
such that
![]() $z\left [ A\right ] \cap w\left [ Y\right ] $
is infinite. Note that it must be the case that
$z\left [ A\right ] \cap w\left [ Y\right ] $
is infinite. Note that it must be the case that
![]() $z\neq w,$
since
$z\neq w,$
since
![]() $A\cap Y$
is finite and w is injective. Let
$A\cap Y$
is finite and w is injective. Let
![]() $p,z_{1},w_{1}\in \mathbb {W}\left ( S\right ) $
such that:
$p,z_{1},w_{1}\in \mathbb {W}\left ( S\right ) $
such that:
-
1.
 $z=pz_{1}.$
$z=pz_{1}.$
-
2.
 $w=pw_{1}.$
$w=pw_{1}.$
-
3.
 $w_{1}^{-1}z_{1}$
is a reduced word.
$w_{1}^{-1}z_{1}$
is a reduced word.
By Lemma 34 we know that
![]() $w^{-1}z\left [ A\right ] \subseteq w_{1}^{-1}z_{1}\left [ A\right ] .$
Since
$w^{-1}z\left [ A\right ] \subseteq w_{1}^{-1}z_{1}\left [ A\right ] .$
Since
![]() $Y\in \mathcal {L(} S,\mathcal {A)}^{\perp },$
we know that
$Y\in \mathcal {L(} S,\mathcal {A)}^{\perp },$
we know that
![]() $w_{1}^{-1}z_{1}\left [ A\right ] \cap Y$
is finite. But since
$w_{1}^{-1}z_{1}\left [ A\right ] \cap Y$
is finite. But since
![]() $z\left [ A\right ] \cap w\left [ Y\right ] $
is infinite, this implies that
$z\left [ A\right ] \cap w\left [ Y\right ] $
is infinite, this implies that
![]() $w^{-1}z\left [ A\right ] \cap Y$
is infinite, which is a contradiction.
$w^{-1}z\left [ A\right ] \cap Y$
is infinite, which is a contradiction.
We now prove the following:
Proposition 46. Let
![]() $(S,\mathcal {A})$
be a nice pair,
$(S,\mathcal {A})$
be a nice pair,
![]() $\left \vert S\right \vert <$
non
$\left \vert S\right \vert <$
non
![]() $\left ( \mathcal {M}\right ) $
and
$\left ( \mathcal {M}\right ) $
and
![]() $X\in \mathcal {L(} S,\mathcal {A)}^{\perp }.$
There is an injective function
$X\in \mathcal {L(} S,\mathcal {A)}^{\perp }.$
There is an injective function
![]() $h:\omega \longrightarrow X$
such that
$h:\omega \longrightarrow X$
such that
![]() $(S\cup \left \{ h\right \} ,\mathcal {A})$
is a nice pair.
$(S\cup \left \{ h\right \} ,\mathcal {A})$
is a nice pair.
Proof Since the size of S is less than non
![]() $\left ( \mathcal {M}\right ) ,$
we can use Proposition 40 and find
$\left ( \mathcal {M}\right ) ,$
we can use Proposition 40 and find
![]() $Y\in \left [ X\right ] ^{\omega }$
such that for every
$Y\in \left [ X\right ] ^{\omega }$
such that for every
![]() $w,z\in \mathbb {W}(S)$
distinct, we have that
$w,z\in \mathbb {W}(S)$
distinct, we have that
![]() $w\left [ Y\right ] \cap z\left [ Y\right ] $
is finite (recall that, in particular, if
$w\left [ Y\right ] \cap z\left [ Y\right ] $
is finite (recall that, in particular, if
![]() $z\neq Id,$
then
$z\neq Id,$
then
![]() $z\left [ Y\right ] \cap Y$
is finite). We now apply Proposition 43 and get an injective function
$z\left [ Y\right ] \cap Y$
is finite). We now apply Proposition 43 and get an injective function
![]() $h:\omega \longrightarrow Y$
such that
$h:\omega \longrightarrow Y$
such that
![]() $S\cup \left \{ h\right \} $
is a partial cofinitary semigroup base. We will show that
$S\cup \left \{ h\right \} $
is a partial cofinitary semigroup base. We will show that
![]() $(S\cup \left \{ h\right \} ,\mathcal {A})$
is a nice pair. We need some preliminary claims that will help us in order to achieve this.
$(S\cup \left \{ h\right \} ,\mathcal {A})$
is a nice pair. We need some preliminary claims that will help us in order to achieve this.
Claim 47. Let
![]() $w\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) .$
If w contains a subword of the form
$w\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) .$
If w contains a subword of the form
![]() $h^{-1}zh$
with
$h^{-1}zh$
with
![]() $z\in \mathbb {W}\left ( S\right ) $
(and
$z\in \mathbb {W}\left ( S\right ) $
(and
![]() $z\neq Id$
), then img
$z\neq Id$
), then img
![]() $\left ( w\right ) $
is finite.
$\left ( w\right ) $
is finite.
It is enough to prove that the domain of
![]() $h^{-1}zh$
is finite. Recall that img
$h^{-1}zh$
is finite. Recall that img
![]() $\left ( h\right ) \subseteq Y$
and
$\left ( h\right ) \subseteq Y$
and
![]() $z\left [ Y\right ] \cap Y$
is finite. Since dom
$z\left [ Y\right ] \cap Y$
is finite. Since dom
![]() $\left ( h^{-1}\right ) =Y,$
it follows that the domain of
$\left ( h^{-1}\right ) =Y,$
it follows that the domain of
![]() $h^{-1}zh$
is finite.
$h^{-1}zh$
is finite.
Claim 48. If
![]() $w\in \mathbb {W}\left ( S\right ) $
and
$w\in \mathbb {W}\left ( S\right ) $
and
![]() $A\in \mathcal {A},$
then
$A\in \mathcal {A},$
then
![]() $h^{-1}w\left [ A\right ] $
is finite.
$h^{-1}w\left [ A\right ] $
is finite.
Since
![]() $Y\in \mathcal {L(}S,\mathcal {A)}^{\perp },$
it follows that
$Y\in \mathcal {L(}S,\mathcal {A)}^{\perp },$
it follows that
![]() $Y\cap w\left [ A\right ] $
is finite. The domain of
$Y\cap w\left [ A\right ] $
is finite. The domain of
![]() $h^{-1}$
is
$h^{-1}$
is
![]() $Y,$
so the claim follows.
$Y,$
so the claim follows.
Note that the elements of
![]() $\mathbb {W}\left ( S\cup \left \{ h\right \} \right ) \setminus \mathbb {W}\left ( S\right ) $
are exactly the words in which h or
$\mathbb {W}\left ( S\cup \left \{ h\right \} \right ) \setminus \mathbb {W}\left ( S\right ) $
are exactly the words in which h or
![]() $h^{-1}$
appear. We now prove the following:
$h^{-1}$
appear. We now prove the following:
Claim 49. If
![]() $w\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) \setminus \mathbb {W}\left ( S\right ) $
and
$w\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) \setminus \mathbb {W}\left ( S\right ) $
and
![]() $A\in \mathcal {A},$
then
$A\in \mathcal {A},$
then
![]() $w\left [ A\right ] \in \mathcal {L(}S,\mathcal {A)}^{\perp }.$
$w\left [ A\right ] \in \mathcal {L(}S,\mathcal {A)}^{\perp }.$
We need to divide the proof by cases:
Case 50.
w contains an
![]() $h.$
$h.$
This case is further divided into subcases.
In case w is of the form
![]() $zh^{-1}phq$
where
$zh^{-1}phq$
where
![]() $z,p,q\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) ,$
then w will contain a subword of the form
$z,p,q\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) ,$
then w will contain a subword of the form
![]() $h^{-1}lh$
with
$h^{-1}lh$
with
![]() $l\in \mathbb {W}\left ( S\right ) .$
By the Claim 47, we get that the image of w is finite.
$l\in \mathbb {W}\left ( S\right ) .$
By the Claim 47, we get that the image of w is finite.
Now, if this was not the case, we can find
![]() $z\in \mathbb {W}\left ( S\right ) $
and
$z\in \mathbb {W}\left ( S\right ) $
and
![]() $p\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) $
such that
$p\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) $
such that
![]() $w=zhp.$
In this case, the image of w is contained in
$w=zhp.$
In this case, the image of w is contained in
![]() $z\left [ Y\right ] .$
By Lemma 45, we know
$z\left [ Y\right ] .$
By Lemma 45, we know
![]() $z\left [ Y\right ] \in \mathcal {L(}S,\mathcal {A)}^{\perp },$
so the result follows.
$z\left [ Y\right ] \in \mathcal {L(}S,\mathcal {A)}^{\perp },$
so the result follows.
Case 51.
w does not contain an
![]() $h.$
$h.$
Follows by Claim 48 since w most contain an
![]() $h^{-1}.$
$h^{-1}.$
We are now in position to prove that
![]() $\mathcal {L(}S\cup \left \{ h\right \} ,\mathcal {A)}$
is an AD family. Let
$\mathcal {L(}S\cup \left \{ h\right \} ,\mathcal {A)}$
is an AD family. Let
![]() $w,z\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) $
and
$w,z\in \mathbb {W}\left ( S\cup \left \{ h\right \} \right ) $
and
![]() $A,B\in \mathcal {A}$
such that
$A,B\in \mathcal {A}$
such that
![]() $w\left [ A\right ] \cap z\left [ B\right ] $
is infinite. Since words are injective, we may assume that w and z does not start in the same way, so
$w\left [ A\right ] \cap z\left [ B\right ] $
is infinite. Since words are injective, we may assume that w and z does not start in the same way, so
![]() $z^{-1}w$
is a reduced word. Since
$z^{-1}w$
is a reduced word. Since
![]() $w\left [ A\right ] \cap z\left [ B\right ] $
is infinite, we get that
$w\left [ A\right ] \cap z\left [ B\right ] $
is infinite, we get that
![]() $z^{-1}w\left [ A\right ] \cap B$
is infinite. By Claim 49, we conclude that
$z^{-1}w\left [ A\right ] \cap B$
is infinite. By Claim 49, we conclude that
![]() $z^{-1} w\in \mathbb {W}\left ( S\right ) .$
Finally, since
$z^{-1} w\in \mathbb {W}\left ( S\right ) .$
Finally, since
![]() $(S,\mathcal {A})$
is a nice pair, it follows that
$(S,\mathcal {A})$
is a nice pair, it follows that
![]() $w=z$
and
$w=z$
and
![]() $A=B.$
$A=B.$
The following is well-known, we include the proof for completeness.
Lemma 52. Let
![]() $\mathcal {A}$
be an AD family of size less than
$\mathcal {A}$
be an AD family of size less than
![]() $\mathfrak {b}$
and
$\mathfrak {b}$
and
![]() $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega }$
pairwise disjoint such that
$\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega }$
pairwise disjoint such that
![]() $X_{n}\in \mathcal {A}^{\perp }$
for every
$X_{n}\in \mathcal {A}^{\perp }$
for every
![]() $n\in \omega .$
There is an increasing function
$n\in \omega .$
There is an increasing function
![]() $g\in \omega ^{\omega }$
such that
$g\in \omega ^{\omega }$
such that
![]() $\bigcup \limits _{n\in \omega }\left ( X_{n}\setminus g\left ( n\right ) \right ) \in \mathcal {A}^{\perp }.$
$\bigcup \limits _{n\in \omega }\left ( X_{n}\setminus g\left ( n\right ) \right ) \in \mathcal {A}^{\perp }.$
Proof Let
![]() $\mathcal {A}=\left \{ A_{\alpha }\mid \alpha <\kappa \right \} $
for some cardinal
$\mathcal {A}=\left \{ A_{\alpha }\mid \alpha <\kappa \right \} $
for some cardinal
![]() $\kappa $
smaller than
$\kappa $
smaller than
![]() $\mathfrak {b}.$
For every
$\mathfrak {b}.$
For every
![]() $\alpha <\mathfrak {b},$
define the function
$\alpha <\mathfrak {b},$
define the function
![]() $f_{\alpha }:\omega \longrightarrow \omega $
such that
$f_{\alpha }:\omega \longrightarrow \omega $
such that
![]() $f_{\alpha }\left ( n\right ) =max\left ( A_{\alpha }\cap X_{n}\right ) +1.$
Since
$f_{\alpha }\left ( n\right ) =max\left ( A_{\alpha }\cap X_{n}\right ) +1.$
Since
![]() $\kappa <\mathfrak {b},$
we know that the family
$\kappa <\mathfrak {b},$
we know that the family
![]() $\mathcal {B}=\left \{ f_{\alpha }\mid \alpha <\kappa \right \} $
is bounded. Any increasing function bounding
$\mathcal {B}=\left \{ f_{\alpha }\mid \alpha <\kappa \right \} $
is bounded. Any increasing function bounding
![]() $\mathcal {B}$
has the desired property.
$\mathcal {B}$
has the desired property.
The following will be useful for getting tight MAD families:
Proposition 53. Let
![]() $(S,\mathcal {A})$
be a good pair such that
$(S,\mathcal {A})$
be a good pair such that
![]() $\left \vert S\right \vert +\left \vert \mathcal {A}\right \vert <\mathfrak {b}.$
Let
$\left \vert S\right \vert +\left \vert \mathcal {A}\right \vert <\mathfrak {b}.$
Let
![]() $\left \{ X_{n}\mid n\in \omega \right \} $
be a family pairwise disjoint infinite sets such that
$\left \{ X_{n}\mid n\in \omega \right \} $
be a family pairwise disjoint infinite sets such that
![]() $X_{n}\in \mathcal {L(}S,\mathcal {A)}^{\perp }$
for every
$X_{n}\in \mathcal {L(}S,\mathcal {A)}^{\perp }$
for every
![]() $n\in \omega .$
There are
$n\in \omega .$
There are
![]() $D_{n}\in \left [ X_{n}\right ] ^{\omega }$
such that if
$D_{n}\in \left [ X_{n}\right ] ^{\omega }$
such that if
![]() $D=\bigcup \limits _{n\in \omega }D_{n},$
then
$D=\bigcup \limits _{n\in \omega }D_{n},$
then
![]() $(S,\mathcal {A}\cup \left \{ D\right \} )$
is a nice pair.
$(S,\mathcal {A}\cup \left \{ D\right \} )$
is a nice pair.
Proof For convenience, let
![]() $\mathcal {B=L(}S,\mathcal {A)}^{\perp }.$
Since
$\mathcal {B=L(}S,\mathcal {A)}^{\perp }.$
Since
![]() $\left \vert \mathcal {B}\right \vert <\mathfrak {b},$
by Lemma 52, we can find an increasing
$\left \vert \mathcal {B}\right \vert <\mathfrak {b},$
by Lemma 52, we can find an increasing
![]() $g\in \omega ^{\omega }$
such that if we let
$g\in \omega ^{\omega }$
such that if we let
![]() $Y_{n} =X_{n}\setminus g\left ( n\right ) $
for every
$Y_{n} =X_{n}\setminus g\left ( n\right ) $
for every
![]() $n\in \omega ,$
then
$n\in \omega ,$
then
![]() $Y=\bigcup \limits _{n\in \omega }Y_{n}$
is in
$Y=\bigcup \limits _{n\in \omega }Y_{n}$
is in
![]() $\mathcal {B}^{\perp }.$
Now, choose
$\mathcal {B}^{\perp }.$
Now, choose
![]() $\mathcal {P}=\left \{ P_{n}\mid n\in \omega \right \} \subseteq \left [ Y\right ] ^{\omega }$
with the following properties:
$\mathcal {P}=\left \{ P_{n}\mid n\in \omega \right \} \subseteq \left [ Y\right ] ^{\omega }$
with the following properties:
-
1.
 $\mathcal {P}$
is a partition of
$\mathcal {P}$
is a partition of
 $Y.$
$Y.$
-
2. Each
 $Y_{n}$
contains infinitely many elements of
$Y_{n}$
contains infinitely many elements of
 $\mathcal {P}.$
$\mathcal {P}.$
-
3. Every element of
 $\mathcal {P}$
is contained in some
$\mathcal {P}$
is contained in some
 $Y_{n}.$
$Y_{n}.$
In other words,
![]() $\mathcal {P}$
is obtained by dividing each
$\mathcal {P}$
is obtained by dividing each
![]() $Y_{n}$
in infinitely many infinite pieces. For each
$Y_{n}$
in infinitely many infinite pieces. For each
![]() $n\in \omega ,$
let
$n\in \omega ,$
let
![]() $l_{n} :\omega \longrightarrow P_{n}$
be its enumerative function.
$l_{n} :\omega \longrightarrow P_{n}$
be its enumerative function.
Let
![]() $w,z\in \mathbb {W}\left [ S\right ] $
be two different words. We define an associated slalom-predictor as follows:
$w,z\in \mathbb {W}\left [ S\right ] $
be two different words. We define an associated slalom-predictor as follows:
![]() $ \begin {array} [c]{c} \pi _{wz}:\omega ^{<\omega }\longrightarrow \left [ \omega \right ] ^{<\omega }. \end {array} $
$ \begin {array} [c]{c} \pi _{wz}:\omega ^{<\omega }\longrightarrow \left [ \omega \right ] ^{<\omega }. \end {array} $
-
1.
 $\pi _{wz}\left ( \emptyset \right ) =0.$
$\pi _{wz}\left ( \emptyset \right ) =0.$
-
2. Let
 $t=\left \langle n_{0},\dots ,n_{m}\right \rangle .$
Define:
$t=\left \langle n_{0},\dots ,n_{m}\right \rangle .$
Define:
 $ \begin {array} [c]{cccc} \pi _{wz}\left ( t\right ) & = & \left \{ n_{0},\dots ,n_{m}\right \} & \cup \\ & & l_{m}^{-1}(z^{-1}w[\left \{ l_{0}\left ( n_{0}\right ) ,\dots ,l_{m}\left ( n_{m}\right ) \right \} ]) & \cup \\ & & l_{m}^{-1}(w^{-1}z[\left \{ l_{0}\left ( n_{0}\right ) ,\dots ,l_{m}\left ( n_{m}\right ) \right \} ]). & \end {array} $
$ \begin {array} [c]{cccc} \pi _{wz}\left ( t\right ) & = & \left \{ n_{0},\dots ,n_{m}\right \} & \cup \\ & & l_{m}^{-1}(z^{-1}w[\left \{ l_{0}\left ( n_{0}\right ) ,\dots ,l_{m}\left ( n_{m}\right ) \right \} ]) & \cup \\ & & l_{m}^{-1}(w^{-1}z[\left \{ l_{0}\left ( n_{0}\right ) ,\dots ,l_{m}\left ( n_{m}\right ) \right \} ]). & \end {array} $
It is easy to see that there is a function
![]() $k:\omega \longrightarrow \omega $
such that each
$k:\omega \longrightarrow \omega $
such that each
![]() $\pi _{wz}$
is a k-slalom predictor. Since
$\pi _{wz}$
is a k-slalom predictor. Since
![]() $\left \vert S\right \vert <\mathfrak {b\leq }$
non
$\left \vert S\right \vert <\mathfrak {b\leq }$
non
![]() $\left ( \mathcal {M}\right ) $
by Theorem 39, we can find an injective
$\left ( \mathcal {M}\right ) $
by Theorem 39, we can find an injective
![]() $h:\omega \longrightarrow \omega $
that escapes from each
$h:\omega \longrightarrow \omega $
that escapes from each
![]() $\pi _{wz}.$
Define
$\pi _{wz}.$
Define
![]() $D=\left \{ l_{n}\left ( h\left ( n\right ) \right ) \mid n\in \omega \right \} $
and
$D=\left \{ l_{n}\left ( h\left ( n\right ) \right ) \mid n\in \omega \right \} $
and
![]() $D_{n}=D\cap Y_{n}$
for every
$D_{n}=D\cap Y_{n}$
for every
![]() $n\in \omega .$
It follows that each
$n\in \omega .$
It follows that each
![]() $D_{n}$
is infinite. Since
$D_{n}$
is infinite. Since
![]() $D\subseteq Y,$
it follows that
$D\subseteq Y,$
it follows that
![]() $D\in \mathcal {B}^{\perp }.$
$D\in \mathcal {B}^{\perp }.$
We now want to prove that
![]() $(S,\mathcal {A}\cup \left \{ D\right \} )$
is a nice pair. We only need to prove that
$(S,\mathcal {A}\cup \left \{ D\right \} )$
is a nice pair. We only need to prove that
![]() $\mathcal {L(}S,\mathcal {A\cup }\left \{ D\right \} \mathcal {)}$
is an AD family. By Lemma 45, we only need to prove that if
$\mathcal {L(}S,\mathcal {A\cup }\left \{ D\right \} \mathcal {)}$
is an AD family. By Lemma 45, we only need to prove that if
![]() $w,z\in \mathbb {W}\left ( S\right ) $
and
$w,z\in \mathbb {W}\left ( S\right ) $
and
![]() $w\neq z,$
then
$w\neq z,$
then
![]() $w\left [ D\right ] \cap z\left [ D\right ] $
is finite. It is enough to prove that the set
$w\left [ D\right ] \cap z\left [ D\right ] $
is finite. It is enough to prove that the set
![]() $L=\left \{ \left ( i,j\right ) \mid wl_{i}h\left ( i\right ) =zl_{j}h\left ( j\right ) \right \} $
is finite. Let
$L=\left \{ \left ( i,j\right ) \mid wl_{i}h\left ( i\right ) =zl_{j}h\left ( j\right ) \right \} $
is finite. Let
![]() $\left ( i,j\right ) \in L.$
$\left ( i,j\right ) \in L.$
We first consider the case in which
![]() $i\neq j.$
Without lost of generality, we may assume that
$i\neq j.$
Without lost of generality, we may assume that
![]() $i<j.$
We get the following:
$i<j.$
We get the following:
 $ \begin {array} [c]{ccc} wl_{i}h\left ( i\right ) =zl_{j}h\left ( j\right ) & \implies & l_{j}h\left ( j\right ) =z^{-1}wl_{i}h\left ( i\right ) \\ & \implies & h\left ( j\right ) =l_{j}^{-1}z^{-1}wl_{i}h\left ( i\right ) \\ & \implies & h\left ( j\right ) \in l_{j}^{-1}\left ( z^{-1}w[\left \{ l_{0}h\left ( 0\right ) ,\dots ,l_{j-1}h\left ( j-1\right ) \right \} ]\right ) \\ & \implies & h\left ( j\right ) \in \pi _{zw}\left ( h\upharpoonright j\right ). \end {array} $
$ \begin {array} [c]{ccc} wl_{i}h\left ( i\right ) =zl_{j}h\left ( j\right ) & \implies & l_{j}h\left ( j\right ) =z^{-1}wl_{i}h\left ( i\right ) \\ & \implies & h\left ( j\right ) =l_{j}^{-1}z^{-1}wl_{i}h\left ( i\right ) \\ & \implies & h\left ( j\right ) \in l_{j}^{-1}\left ( z^{-1}w[\left \{ l_{0}h\left ( 0\right ) ,\dots ,l_{j-1}h\left ( j-1\right ) \right \} ]\right ) \\ & \implies & h\left ( j\right ) \in \pi _{zw}\left ( h\upharpoonright j\right ). \end {array} $
Since h escapes from
![]() $\pi _{zw},$
we conclude that there are only finitely many pairs
$\pi _{zw},$
we conclude that there are only finitely many pairs
![]() $\left ( i,j\right ) $
that fall in this case.
$\left ( i,j\right ) $
that fall in this case.
Finally, if
![]() $i=j,$
then
$i=j,$
then
![]() $w\left ( l_{i}h\left ( i\right ) \right ) =z\left ( l_{i}h\left ( i\right ) \right ) .$
Since w and z are almost disjoint, only finitely many pairs
$w\left ( l_{i}h\left ( i\right ) \right ) =z\left ( l_{i}h\left ( i\right ) \right ) .$
Since w and z are almost disjoint, only finitely many pairs
![]() $\left ( i,j\right ) $
fall in this case. This finishes the proof.
$\left ( i,j\right ) $
fall in this case. This finishes the proof.
We will use the following lemma several times:
Lemma 54. Let
![]() $(S,\mathcal {A})$
be a nice pair such that for every
$(S,\mathcal {A})$
be a nice pair such that for every
![]() $X\in \mathcal {L} (S,\mathcal {A})^{+},$
there is
$X\in \mathcal {L} (S,\mathcal {A})^{+},$
there is
![]() $f:\omega \longrightarrow X$
such that
$f:\omega \longrightarrow X$
such that
![]() $f\in S.$
The family
$f\in S.$
The family
![]() $\mathcal {L}(S,\mathcal {A})$
is a Katětov uniform MAD family.
$\mathcal {L}(S,\mathcal {A})$
is a Katětov uniform MAD family.
Proof Let
![]() $\mathcal {B}=\mathcal {L}(S,\mathcal {A}).$
Since
$\mathcal {B}=\mathcal {L}(S,\mathcal {A}).$
Since
![]() $\mathcal {A}\neq \emptyset ,$
the hypothesis implies that every set in
$\mathcal {A}\neq \emptyset ,$
the hypothesis implies that every set in
![]() $\mathcal {I(B)}^{+}$
contains an element of
$\mathcal {I(B)}^{+}$
contains an element of
![]() $\mathcal {B}.$
This implies that
$\mathcal {B}.$
This implies that
![]() $\mathcal {B}$
is maximal (in this way,
$\mathcal {B}$
is maximal (in this way,
![]() $\mathcal {B}$
is a completely separable MAD family). We now prove that
$\mathcal {B}$
is a completely separable MAD family). We now prove that
![]() $\mathcal {B}$
is Katětov uniform.
$\mathcal {B}$
is Katětov uniform.
Let
![]() $X\in \mathcal {B}^{+},$
we need to prove that
$X\in \mathcal {B}^{+},$
we need to prove that
![]() $\mathcal {B}\upharpoonright X \leq _{\textsf {K}}\mathcal {B}.$
By the hypothesis, we know there is
$\mathcal {B}\upharpoonright X \leq _{\textsf {K}}\mathcal {B}.$
By the hypothesis, we know there is
![]() $f:\omega \longrightarrow X$
such that
$f:\omega \longrightarrow X$
such that
![]() $f\in S.$
We will show that f is a Katětov function from
$f\in S.$
We will show that f is a Katětov function from
![]() $(\omega ,\mathcal {B})$
to
$(\omega ,\mathcal {B})$
to
![]() $(X,\mathcal {B} \upharpoonright X).$
We will use Lemma 11. Let
$(X,\mathcal {B} \upharpoonright X).$
We will use Lemma 11. Let
![]() $D\in \mathcal {B}^{+},$
we need to prove that
$D\in \mathcal {B}^{+},$
we need to prove that
![]() $f\left [ D\right ] \in \mathcal {B}^{+}.$
Since
$f\left [ D\right ] \in \mathcal {B}^{+}.$
Since
![]() $\mathcal {B}$
is completely separable, there are
$\mathcal {B}$
is completely separable, there are
![]() $\left \{ A_{n}\mid n\in \omega \right \} \subseteq \mathcal {A}$
and
$\left \{ A_{n}\mid n\in \omega \right \} \subseteq \mathcal {A}$
and
![]() $\left \{ w_{n}\mid n\in \omega \right \} \subseteq \mathbb {W}\left ( S\right ) $
such that
$\left \{ w_{n}\mid n\in \omega \right \} \subseteq \mathbb {W}\left ( S\right ) $
such that
![]() $w_{n}\left [ A_{n}\right ] \subseteq D$
and each
$w_{n}\left [ A_{n}\right ] \subseteq D$
and each
![]() $w_{n}\left [ A_{n}\right ] $
is infinite. Without lost of generality, we may assume that either all
$w_{n}\left [ A_{n}\right ] $
is infinite. Without lost of generality, we may assume that either all
![]() $w_{n}$
start with
$w_{n}$
start with
![]() $f^{-1}$
or none of them do.
$f^{-1}$
or none of them do.
In case that none of them start with
![]() $f^{-1},$
we get that
$f^{-1},$
we get that
![]() $fw_{n}$
is a reduced word, so
$fw_{n}$
is a reduced word, so
![]() $fw_{n}\left [ A_{n}\right ] \in \mathcal {B}$
and clearly
$fw_{n}\left [ A_{n}\right ] \in \mathcal {B}$
and clearly
![]() $fw_{n}\left [ A_{n}\right ] \subseteq f\left [ D\right ] $
for every
$fw_{n}\left [ A_{n}\right ] \subseteq f\left [ D\right ] $
for every
![]() $n\in \omega .$
Now assume that
$n\in \omega .$
Now assume that
![]() $w_{n}=f^{-1}z_{n}$
for some
$w_{n}=f^{-1}z_{n}$
for some
![]() $z_{n}\in \mathbb {W}(S).$
It follows that each
$z_{n}\in \mathbb {W}(S).$
It follows that each
![]() $z_{n}\left [ A_{n}\right ] $
has infinite intersection with
$z_{n}\left [ A_{n}\right ] $
has infinite intersection with
![]() $f\left [ D\right ] .$
This finishes the proof.
$f\left [ D\right ] .$
This finishes the proof.
Let
![]() $\mathcal {P}$
be a property that MAD families may or not may have. We say that MAD families with property
$\mathcal {P}$
be a property that MAD families may or not may have. We say that MAD families with property
![]() $\mathcal {P}$
exist generically, if every AD family of size less than
$\mathcal {P}$
exist generically, if every AD family of size less than
![]() $\mathfrak {c}$
can be extended to a MAD family with property
$\mathfrak {c}$
can be extended to a MAD family with property
![]() $\mathcal {P}.$
In [Reference Guzmán and Hrušák32] the generic existence of several types of MAD families was studied. The generic existence of ultrafilters has been extensively studied (see, for example, [Reference Brendle and Flašková6, Reference Cancino-Manríquez11, Reference Canjar13, Reference Guzmán and Hrušák29], among others).
$\mathcal {P}.$
In [Reference Guzmán and Hrušák32] the generic existence of several types of MAD families was studied. The generic existence of ultrafilters has been extensively studied (see, for example, [Reference Brendle and Flašková6, Reference Cancino-Manríquez11, Reference Canjar13, Reference Guzmán and Hrušák29], among others).
We can now prove the main result of the section:
Theorem 55.
![]() $\mathfrak {b=c}$
implies that tight Katětov maximal MAD families exist generically.
$\mathfrak {b=c}$
implies that tight Katětov maximal MAD families exist generically.
Proof Let
![]() $\mathcal {A}_{0}$
be an AD of size less than
$\mathcal {A}_{0}$
be an AD of size less than
![]() $\mathfrak {c}.$
Fix U and T subsets of
$\mathfrak {c}.$
Fix U and T subsets of
![]() $\mathfrak {c}$
with the following properties:
$\mathfrak {c}$
with the following properties:
-
1.
 $\mathfrak {c}=U\cup T.$
$\mathfrak {c}=U\cup T.$
-
2.
 $U\cap T=\emptyset .$
$U\cap T=\emptyset .$
-
3.
 $\left \vert U\right \vert =\left \vert T\right \vert =\mathfrak {c}.$
$\left \vert U\right \vert =\left \vert T\right \vert =\mathfrak {c}.$
Fix an enumeration
![]() $\left [ \omega \right ] ^{\omega }=\left \{ X_{\alpha } \mid \alpha \in U\right \} $
and
$\left [ \omega \right ] ^{\omega }=\left \{ X_{\alpha } \mid \alpha \in U\right \} $
and
![]() $\left ( \left [ \omega \right ] ^{\omega }\right ) ^{\omega }=\{\overline {Y_{\alpha }}\mid \alpha \in T\}$
where
$\left ( \left [ \omega \right ] ^{\omega }\right ) ^{\omega }=\{\overline {Y_{\alpha }}\mid \alpha \in T\}$
where
![]() $\overline {Y_{\alpha }}=\left \{ Y_{\alpha }\left ( n\right ) \mid n\in \omega \right \} .$
We will now recursively define
$\overline {Y_{\alpha }}=\left \{ Y_{\alpha }\left ( n\right ) \mid n\in \omega \right \} .$
We will now recursively define
![]() $\{\mathcal {A}_{\alpha } \mid \alpha <\mathfrak {c}\}$
and
$\{\mathcal {A}_{\alpha } \mid \alpha <\mathfrak {c}\}$
and
![]() $\{S_{\alpha }\mid \alpha <\mathfrak {c}\}$
such that for every
$\{S_{\alpha }\mid \alpha <\mathfrak {c}\}$
such that for every
![]() $\alpha <\mathfrak {c},$
the following holds:
$\alpha <\mathfrak {c},$
the following holds:
-
1.
 $\mathcal {A}_{0}=\mathcal {A}$
and
$\mathcal {A}_{0}=\mathcal {A}$
and
 $S_{0}=\left \{ Id\right \} .$
$S_{0}=\left \{ Id\right \} .$
-
2.
 $\mathcal {A}_{\alpha }$
is an AD family and
$\mathcal {A}_{\alpha }$
is an AD family and
 $S_{\alpha }$
is a partial cofinitary semigroup base.
$S_{\alpha }$
is a partial cofinitary semigroup base. -
3.
 $(\mathcal {A}_{\alpha },S_{\alpha })$
is a nice pair.
$(\mathcal {A}_{\alpha },S_{\alpha })$
is a nice pair. -
4. If
 $\beta <\alpha ,$
then
$\beta <\alpha ,$
then
 $\mathcal {A}_{\beta }\subseteq \mathcal {A} _{\alpha }$
and
$\mathcal {A}_{\beta }\subseteq \mathcal {A} _{\alpha }$
and
 $S_{\beta }\subseteq S_{\alpha }.$
$S_{\beta }\subseteq S_{\alpha }.$
-
5.
 $\left \vert \mathcal {A}_{\alpha }\right \vert +\left \vert S_{\alpha }\right \vert \leq \left \vert \mathcal {A}_{0}\right \vert +\left \vert \alpha \right \vert +\omega .$
$\left \vert \mathcal {A}_{\alpha }\right \vert +\left \vert S_{\alpha }\right \vert \leq \left \vert \mathcal {A}_{0}\right \vert +\left \vert \alpha \right \vert +\omega .$
-
6. If
 $\alpha $
is a limit ordinal, then
$\alpha $
is a limit ordinal, then
 $\mathcal {A}_{\alpha } =\bigcup \limits _{\beta <\alpha }\mathcal {A}_{\beta }$
and
$\mathcal {A}_{\alpha } =\bigcup \limits _{\beta <\alpha }\mathcal {A}_{\beta }$
and
 $S_{\alpha } =\bigcup \limits _{\beta <\alpha }S_{\beta }.$
$S_{\alpha } =\bigcup \limits _{\beta <\alpha }S_{\beta }.$
-
7. If
 $\alpha \in T$
and each
$\alpha \in T$
and each
 $Y_{\alpha }\left ( n\right ) \in \mathcal {I(L}\left ( S_{\alpha },\mathcal {A}_{\alpha }\right ) \mathcal {)}^{+},$
then there is
$Y_{\alpha }\left ( n\right ) \in \mathcal {I(L}\left ( S_{\alpha },\mathcal {A}_{\alpha }\right ) \mathcal {)}^{+},$
then there is
 $A\in \mathcal {A}_{\alpha +1}$
such that
$A\in \mathcal {A}_{\alpha +1}$
such that
 $A\cap Y_{\alpha }\left ( n\right ) $
is infinite for every
$A\cap Y_{\alpha }\left ( n\right ) $
is infinite for every
 $n\in \omega .$
$n\in \omega .$
-
8. If
 $\alpha \in U$
and
$\alpha \in U$
and
 $X_{\alpha }\in \mathcal {I(L(}S_{\alpha } ,\mathcal {A}_{\alpha }\mathcal {))}^{+},$
then there is
$X_{\alpha }\in \mathcal {I(L(}S_{\alpha } ,\mathcal {A}_{\alpha }\mathcal {))}^{+},$
then there is
 $f\in S_{\alpha +1}$
such that
$f\in S_{\alpha +1}$
such that
 $f:\omega \longrightarrow X_{\alpha }.$
$f:\omega \longrightarrow X_{\alpha }.$
Let
![]() $\alpha <\mathfrak {c}$
and assume we have already defined
$\alpha <\mathfrak {c}$
and assume we have already defined
![]() $\{(\mathcal {A} _{\xi },S_{\xi })\mid \xi \leq \alpha \}.$
We will now define
$\{(\mathcal {A} _{\xi },S_{\xi })\mid \xi \leq \alpha \}.$
We will now define
![]() $\mathcal {A} _{\alpha +1}$
and
$\mathcal {A} _{\alpha +1}$
and
![]() $S_{\alpha +1}$
(recall that at limit steps we just need to take unions). There are two cases to consider.
$S_{\alpha +1}$
(recall that at limit steps we just need to take unions). There are two cases to consider.
Case 56.
![]() $\alpha \in T.$
$\alpha \in T.$
If there is
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $Y_{\alpha }\left ( n\right ) \notin \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+},$
we just define
$Y_{\alpha }\left ( n\right ) \notin \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+},$
we just define
![]() $\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }$
and
$\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }$
and
![]() $S_{\alpha +1}=S_{\alpha }.$
Now, assume that
$S_{\alpha +1}=S_{\alpha }.$
Now, assume that
![]() $Y_{\alpha }\left ( n\right ) \in \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+}$
for every
$Y_{\alpha }\left ( n\right ) \in \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+}$
for every
![]() $n\in \omega .$
Since the size of
$n\in \omega .$
Since the size of
![]() $\mathcal {L}\left ( \mathcal {A} _{\alpha },S_{\alpha }\right ) $
is less than
$\mathcal {L}\left ( \mathcal {A} _{\alpha },S_{\alpha }\right ) $
is less than
![]() $\mathfrak {a=c},$
we can find
$\mathfrak {a=c},$
we can find
![]() $\left \{ Z_{n}\mid n\in \omega \right \} $
such that for every
$\left \{ Z_{n}\mid n\in \omega \right \} $
such that for every
![]() $n\in \omega ,$
the following holds:
$n\in \omega ,$
the following holds:
-
1.
 $Z_{n}\subseteq Y_{\alpha }\left ( n\right ) $
is infinite.
$Z_{n}\subseteq Y_{\alpha }\left ( n\right ) $
is infinite. -
2.
 $Z_{n}\in \mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) ^{\perp }.$
$Z_{n}\in \mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) ^{\perp }.$
-
3.
 $Z_{n}\cap Z_{m}=\emptyset $
whenever
$Z_{n}\cap Z_{m}=\emptyset $
whenever
 $n\neq m.$
$n\neq m.$
Since both
![]() $\mathcal {A}_{\alpha }$
and
$\mathcal {A}_{\alpha }$
and
![]() $S_{\alpha }$
have size less than
$S_{\alpha }$
have size less than
![]() $\mathfrak {b=c},$
we can apply Proposition 53 and find
$\mathfrak {b=c},$
we can apply Proposition 53 and find
![]() $D\in \left [ \omega \right ] ^{\omega }$
such that D has infinite intersection with all the
$D\in \left [ \omega \right ] ^{\omega }$
such that D has infinite intersection with all the
![]() $Z_{n}$
and
$Z_{n}$
and
![]() $(S_{\alpha },\mathcal {A}_{\alpha }\cup \left \{ D\right \} )$
is a nice pair. We now define
$(S_{\alpha },\mathcal {A}_{\alpha }\cup \left \{ D\right \} )$
is a nice pair. We now define
![]() $\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }\cup \left \{ D\right \} $
and
$\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }\cup \left \{ D\right \} $
and
![]() $S_{\alpha +1}=S_{\alpha }.$
$S_{\alpha +1}=S_{\alpha }.$
Case 57.
![]() $\alpha \in U.$
$\alpha \in U.$
If
![]() $X_{\alpha }\notin \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+},$
we just define
$X_{\alpha }\notin \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+},$
we just define
![]() $\mathcal {A}_{\alpha +1} =\mathcal {A}_{\alpha }$
and
$\mathcal {A}_{\alpha +1} =\mathcal {A}_{\alpha }$
and
![]() $S_{\alpha +1}=S_{\alpha }.$
Assume that
$S_{\alpha +1}=S_{\alpha }.$
Assume that
![]() $X_{\alpha }\in \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+}.$
Since the size of
$X_{\alpha }\in \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+}.$
Since the size of
![]() $\mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) $
is less than
$\mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) $
is less than
![]() $\mathfrak {a=c},$
we can find
$\mathfrak {a=c},$
we can find
![]() $Z\in \left [ X\right ] ^{\omega }$
such that
$Z\in \left [ X\right ] ^{\omega }$
such that
![]() $Z\in \mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) ^{\perp }.$
Moreover, we know that the size of
$Z\in \mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) ^{\perp }.$
Moreover, we know that the size of
![]() $S_{\alpha }$
is less than non
$S_{\alpha }$
is less than non
![]() $\left ( \mathcal {M}\right ) =\mathfrak {c},$
so by Proposition 46, we know there is an injective function
$\left ( \mathcal {M}\right ) =\mathfrak {c},$
so by Proposition 46, we know there is an injective function
![]() $f:\omega \longrightarrow Z$
such that
$f:\omega \longrightarrow Z$
such that
![]() $(S_{\alpha }\cup \left \{ f\right \} ,\mathcal {A}_{\alpha })$
is a nice pair. Define
$(S_{\alpha }\cup \left \{ f\right \} ,\mathcal {A}_{\alpha })$
is a nice pair. Define
![]() $\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }$
and
$\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }$
and
![]() $S_{\alpha +1}=S_{\alpha }\cup \left \{ f\right \} .$
$S_{\alpha +1}=S_{\alpha }\cup \left \{ f\right \} .$
This finishes the construction. Define
![]() $S_{\mathfrak {c}}=\bigcup \limits _{\alpha <\mathfrak {c}}S_{\alpha }$
and
$S_{\mathfrak {c}}=\bigcup \limits _{\alpha <\mathfrak {c}}S_{\alpha }$
and
![]() $\mathcal {A}_{\mathfrak {c} }=\bigcup \limits _{\alpha <\mathfrak {c}}\mathcal {A}_{\alpha }.$
It is clear that
$\mathcal {A}_{\mathfrak {c} }=\bigcup \limits _{\alpha <\mathfrak {c}}\mathcal {A}_{\alpha }.$
It is clear that
![]() $(S_{\mathfrak {c}},\mathcal {A}_{c})$
is a nice pair. Let
$(S_{\mathfrak {c}},\mathcal {A}_{c})$
is a nice pair. Let
![]() $\mathcal {B=L} (S_{\mathfrak {c}},\mathcal {A}_{c}).$
By Lemma 54, it follows that
$\mathcal {B=L} (S_{\mathfrak {c}},\mathcal {A}_{c}).$
By Lemma 54, it follows that
![]() $\mathcal {B}$
is a Katětov uniform MAD family. It is also clear that
$\mathcal {B}$
is a Katětov uniform MAD family. It is also clear that
![]() $\mathcal {B}$
is tight. By Proposition 30,
$\mathcal {B}$
is tight. By Proposition 30,
![]() $\mathcal {B}$
is a Katětov maximal MAD family.
$\mathcal {B}$
is a Katětov maximal MAD family.
In [Reference Guzmán and Hrušák32], it was proved that
![]() $\mathfrak {b=c}$
is equivalent to the generic existence of tight MAD families. We conclude the following:
$\mathfrak {b=c}$
is equivalent to the generic existence of tight MAD families. We conclude the following:
Corollary 58. Tight, Katětov maximal MAD families exist generically if and only if
![]() $\mathfrak {b=c}.$
$\mathfrak {b=c}.$
If we are only interested in Katětov uniform MAD families, we can use a weaker hypothesis than the one in Theorem 55:
Theorem 59.
non
![]() $\left ( \mathcal {M}\right ) =\mathfrak {a=c}$
implies that Katětov uniform MAD families exist generically.
$\left ( \mathcal {M}\right ) =\mathfrak {a=c}$
implies that Katětov uniform MAD families exist generically.
Proof Let
![]() $\mathcal {A}$
be an AD of size less than
$\mathcal {A}$
be an AD of size less than
![]() $\mathfrak {c}.$
We can assume that
$\mathfrak {c}.$
We can assume that
![]() $\mathcal {A}$
is at least countable. Fix an enumeration
$\mathcal {A}$
is at least countable. Fix an enumeration
![]() $\left [ \omega \right ] ^{\omega }=\left \{ X_{\alpha }\mid \alpha \in \mathfrak {c}\right \} .$
We will now recursively define
$\left [ \omega \right ] ^{\omega }=\left \{ X_{\alpha }\mid \alpha \in \mathfrak {c}\right \} .$
We will now recursively define
![]() $\{S_{\alpha }\mid \alpha <\mathfrak {c}\}$
such that for every
$\{S_{\alpha }\mid \alpha <\mathfrak {c}\}$
such that for every
![]() $\alpha <\mathfrak {c},$
the following holds:
$\alpha <\mathfrak {c},$
the following holds:
-
1.
 $S_{0}=\left \{ Id\right \} .$
$S_{0}=\left \{ Id\right \} .$
-
2.
 $S_{\alpha }$
is a partial cofinitary semigroup base.
$S_{\alpha }$
is a partial cofinitary semigroup base. -
3.
 $(\mathcal {A},S_{\alpha })$
is a nice pair.
$(\mathcal {A},S_{\alpha })$
is a nice pair. -
4. If
 $\beta <\alpha ,$
then
$\beta <\alpha ,$
then
 $S_{\beta }\subseteq S_{\alpha }.$
$S_{\beta }\subseteq S_{\alpha }.$
-
5.
 $\left \vert \mathcal {A}\right \vert +\left \vert S_{\alpha }\right \vert \leq \left \vert \mathcal {A}\right \vert +\left \vert \alpha \right \vert +\omega .$
$\left \vert \mathcal {A}\right \vert +\left \vert S_{\alpha }\right \vert \leq \left \vert \mathcal {A}\right \vert +\left \vert \alpha \right \vert +\omega .$
-
6. If
 $\alpha $
is a limit ordinal, then
$\alpha $
is a limit ordinal, then
 $S_{\alpha }=\bigcup \limits _{\beta <\alpha }S_{\beta }.$
$S_{\alpha }=\bigcup \limits _{\beta <\alpha }S_{\beta }.$
-
7. If
 $X_{\alpha }\in \mathcal {I(L}\left ( S_{\alpha },\mathcal {A}\right ) \mathcal {)}^{+},$
then there is
$X_{\alpha }\in \mathcal {I(L}\left ( S_{\alpha },\mathcal {A}\right ) \mathcal {)}^{+},$
then there is
 $f\in S_{\alpha +1}$
such that
$f\in S_{\alpha +1}$
such that
 $f:\omega \longrightarrow X_{\alpha }.$
$f:\omega \longrightarrow X_{\alpha }.$
Let
![]() $\alpha <\mathfrak {c}$
and assume we have already defined
$\alpha <\mathfrak {c}$
and assume we have already defined
![]() $S_{\xi }$
for
$S_{\xi }$
for
![]() $\xi \leq \alpha ,$
we will now define
$\xi \leq \alpha ,$
we will now define
![]() $S_{\alpha +1}$
. We simply use the same construction as in the case that
$S_{\alpha +1}$
. We simply use the same construction as in the case that
![]() $\alpha \in U$
of Theorem 55.
$\alpha \in U$
of Theorem 55.
Define
![]() $S=\bigcup \limits _{\alpha <\mathfrak {c}}S_{\alpha }$
. It is clear that
$S=\bigcup \limits _{\alpha <\mathfrak {c}}S_{\alpha }$
. It is clear that
![]() $(S,\mathcal {A})$
is a nice pair. Let
$(S,\mathcal {A})$
is a nice pair. Let
![]() $\mathcal {B=L}(S,\mathcal {A}).$
By Lemma 54, it follows that
$\mathcal {B=L}(S,\mathcal {A}).$
By Lemma 54, it follows that
![]() $\mathcal {B}$
is a Katětov uniform MAD family.
$\mathcal {B}$
is a Katětov uniform MAD family.
The previous result was proved by García-Ferreira and Hrušák assuming
![]() $\mathfrak {t=c}$
(see [Reference Hrušák and Ferreira40]). It is worth noting that it is consistent that
$\mathfrak {t=c}$
(see [Reference Hrušák and Ferreira40]). It is worth noting that it is consistent that
![]() $\mathfrak {b<a=}$
non
$\mathfrak {b<a=}$
non
![]() $\left ( \mathcal {M}\right ) =\mathfrak {c}.$
This is the case in the following models:
$\left ( \mathcal {M}\right ) =\mathfrak {c}.$
This is the case in the following models:
-
1. Shelah’s first model of
 $\mathfrak {b<a}$
(see the book [Reference Shelah60]; see also [Reference Brendle and Raghavan8, Reference Guzmán, Hrušák and Martínez-Celis31, Reference Guzmán and Kalajdzievski30]).
$\mathfrak {b<a}$
(see the book [Reference Shelah60]; see also [Reference Brendle and Raghavan8, Reference Guzmán, Hrušák and Martínez-Celis31, Reference Guzmán and Kalajdzievski30]). -
2. Brendle’s finite support model of
 $\mathfrak {b<a}$
(see [Reference Brendle5]).
$\mathfrak {b<a}$
(see [Reference Brendle5]). -
3. Dow’s model in which
 $\mathfrak {b<s=a}$
and every compact space of countable tightness and weight
$\mathfrak {b<s=a}$
and every compact space of countable tightness and weight
 $\omega _{1}$
is Fréchet (see [Reference Dow18]).
$\omega _{1}$
is Fréchet (see [Reference Dow18]). -
4. The model of
 $\mathfrak {u<a}$
in [Reference Guzmán, Hrušák, Martínez and Ramos30].
$\mathfrak {u<a}$
in [Reference Guzmán, Hrušák, Martínez and Ramos30].
It is not clear if there are Katětov maximal MAD families in the models above. We also do not know if the generic existence of Katětov uniform MAD families is equivalent to non
![]() $\left ( \mathcal {M}\right ) =\mathfrak {a=c}.$
$\left ( \mathcal {M}\right ) =\mathfrak {a=c}.$
6 Two more constructions
One would expect that Katětov maximal MAD families are relatively high in the Katětov order. The purpose of this section is to show that, perhaps paradoxically, this might not be the case. We will look at two properties: Sacks indestructibility and Laflammeness. Both of this properties serve as measures of how high a MAD family is positioned in the Katětov order. We will show that (consistently) Katětov maximal MAD families may fail both. We will first explain why we are interesting in this two properties.
For a MAD family, being high in the Katětov order is necessary to have some sort of forcing indestructibility. For this reason, we may wonder if Katětov maximal MAD families have some indestructibility properties. We will show that (consistently) this is not the case. We will prove that it is consistent that there is a weakly tight, Katětov maximal MAD family that is destructible by Sacks forcing.
Recall from the preliminaries section, the mapping
![]() $\pi :\mathcal {P}\left ( 2^{<\omega }\right ) \longrightarrow \mathcal {P}\left ( 2^{\omega }\right ) $
is define as
$\pi :\mathcal {P}\left ( 2^{<\omega }\right ) \longrightarrow \mathcal {P}\left ( 2^{\omega }\right ) $
is define as
![]() $\pi \left ( a\right ) =\{x\in 2^{\omega }\mid \exists ^{\infty }s\in a\left ( s\subseteq x\right ) \}.$
The ideal ctble is the ideal of all finite or countable subsets of
$\pi \left ( a\right ) =\{x\in 2^{\omega }\mid \exists ^{\infty }s\in a\left ( s\subseteq x\right ) \}.$
The ideal ctble is the ideal of all finite or countable subsets of
![]() $2^{\omega }$
and its trace ideal is defined as tr(ctble)
$2^{\omega }$
and its trace ideal is defined as tr(ctble)
![]() $=\{a\subseteq 2^{\omega }\mid \pi \left ( a\right ) \in $
ctble
$=\{a\subseteq 2^{\omega }\mid \pi \left ( a\right ) \in $
ctble
![]() $\}.$
Trace ideals were first introduced by Brendle. The reason we were interested in finding Katětov maximal MAD families that are destructible by Sacks forcing is because of the following (particular case of a) theorem of Brendle and Yatabe:Footnote
5
$\}.$
Trace ideals were first introduced by Brendle. The reason we were interested in finding Katětov maximal MAD families that are destructible by Sacks forcing is because of the following (particular case of a) theorem of Brendle and Yatabe:Footnote
5
Theorem 60 [Reference Brendle, Spinas and Zhang9].
Let
![]() $\mathcal {A}$
be a MAD family. The following statements are equivalent
$\mathcal {A}$
be a MAD family. The following statements are equivalent
![]() $:$
$:$
-
1. Sacks forcing destroys
 $\mathcal {A}.$
$\mathcal {A}.$
-
2. Every forcing that adds a new real destroys
 $\mathcal {A}.$
$\mathcal {A}.$
-
3.
 $\mathcal {A}\leq _{\textsf {K}}$
tr(ctble).
$\mathcal {A}\leq _{\textsf {K}}$
tr(ctble).
The following property was first consider in [Reference Laflamme52] by Laflamme:
Definition 61. Let
![]() $\mathcal {A}$
be a MAD family. We say
$\mathcal {A}$
be a MAD family. We say
![]() $\mathcal {A}$
is a Laflamme family if there is no
$\mathcal {A}$
is a Laflamme family if there is no
![]() $F_{\sigma }$
-ideal
$F_{\sigma }$
-ideal
![]() $\mathcal {I}$
such that
$\mathcal {I}$
such that
![]() $\mathcal {I}(\mathcal {A})\subseteq \mathcal {I}.$
$\mathcal {I}(\mathcal {A})\subseteq \mathcal {I}.$
An interesting features of non-Laflamme families is that they can be destroyed by a forcing that does not add unbounded reals (see [Reference Hernández-Hernández and Hrušák35, Reference Laflamme52, Reference Zapletal62]). Laflamme MAD families play a fundamental role in some of the proofs of the consistency of the inequality
![]() $\mathfrak {b<a}$
(see [Reference Brendle5, Reference Brendle and Raghavan8, Reference Guzmán, Hrušák and Martínez-Celis31, Reference Guzmán and Kalajdzievski30, Reference Shelah60]). In [Reference Laflamme52] Laflamme proved that CH implied that there is a Laflamme MAD family. This was later improved by Minami and Sakai in [Reference Minami and Sakai57] where they showed that
$\mathfrak {b<a}$
(see [Reference Brendle5, Reference Brendle and Raghavan8, Reference Guzmán, Hrušák and Martínez-Celis31, Reference Guzmán and Kalajdzievski30, Reference Shelah60]). In [Reference Laflamme52] Laflamme proved that CH implied that there is a Laflamme MAD family. This was later improved by Minami and Sakai in [Reference Minami and Sakai57] where they showed that
![]() $\mathfrak {p=c}$
is enough. The following result may be consider folklore:
$\mathfrak {p=c}$
is enough. The following result may be consider folklore:
Lemma 62. Let
![]() $\mathcal {A}$
be a MAD family. The following are equivalent
$\mathcal {A}$
be a MAD family. The following are equivalent
![]() $:$
$:$
-
1.
 $\mathcal {A}$
is a Laflamme MAD family.
$\mathcal {A}$
is a Laflamme MAD family. -
2. There is no
 $F_{\sigma }$
-ideal
$F_{\sigma }$
-ideal
 $\mathcal {I}$
such that
$\mathcal {I}$
such that
 $\mathcal {A}$
$\mathcal {A}$
 $\leq _{\textsf {K}}\mathcal {I}.$
$\leq _{\textsf {K}}\mathcal {I}.$
For this reason, Laflamme MAD families most be high in the Katětov order. Once again, we might be tempted to think that Katětov maximal MAD families must be Laflamme. We will show that this is not the case.
We will now develop some general results for constructing Katětov maximal AD families contained in a given ideal. We give two applications, but we hope there will be more applications in the future.
Lemma 63. Let
![]() $\mathcal {I}$
be a tall ideal,
$\mathcal {I}$
be a tall ideal,
![]() $(S,\mathcal {A})$
a nice pair such that
$(S,\mathcal {A})$
a nice pair such that
![]() $\left \vert S\right \vert <\mathfrak {h}$
and
$\left \vert S\right \vert <\mathfrak {h}$
and
![]() $\mathcal {L(} S,\mathcal {A)\subseteq I}.$
Let
$\mathcal {L(} S,\mathcal {A)\subseteq I}.$
Let
![]() $X\in \mathcal {L(}S,\mathcal {A)}^{\perp }.$
There is an injective function
$X\in \mathcal {L(}S,\mathcal {A)}^{\perp }.$
There is an injective function
![]() $f:\omega \longrightarrow X$
such that
$f:\omega \longrightarrow X$
such that
![]() $(S\cup \left \{ f\right \} ,\mathcal {A})$
is a nice pair and
$(S\cup \left \{ f\right \} ,\mathcal {A})$
is a nice pair and
![]() $\mathcal {L(} S\cup \left \{ f\right \} ,\mathcal {A)\subseteq I}.$
$\mathcal {L(} S\cup \left \{ f\right \} ,\mathcal {A)\subseteq I}.$
Proof For every word
![]() $w\in \mathbb {W}\left ( S\right ) ,$
define
$w\in \mathbb {W}\left ( S\right ) ,$
define
![]() $D_{w}=\{Y\in \left [ X\right ] ^{\omega }\mid w\left [ Y\right ] \in \mathcal {I}\}.$
Since
$D_{w}=\{Y\in \left [ X\right ] ^{\omega }\mid w\left [ Y\right ] \in \mathcal {I}\}.$
Since
![]() $\mathcal {I}$
is a tall ideal, it follows that each
$\mathcal {I}$
is a tall ideal, it follows that each
![]() $D_{w}$
is an open dense subset of
$D_{w}$
is an open dense subset of
![]() $\left [ \omega \right ] ^{\omega }.$
We know that
$\left [ \omega \right ] ^{\omega }.$
We know that
![]() $\left \vert S\right \vert <\mathfrak {h},$
so we can find
$\left \vert S\right \vert <\mathfrak {h},$
so we can find
![]() $X_{0}\in \left [ X\right ] ^{\omega }$
such that
$X_{0}\in \left [ X\right ] ^{\omega }$
such that
![]() $w\left [ X_{0}\right ] \in \mathcal {I}$
for every
$w\left [ X_{0}\right ] \in \mathcal {I}$
for every
![]() $w\in \mathbb {W}\left ( S\right ) .$
Now, since the size of S is less than non
$w\in \mathbb {W}\left ( S\right ) .$
Now, since the size of S is less than non
![]() $\left ( \mathcal {M}\right ) ,$
we can use Proposition 40 and find
$\left ( \mathcal {M}\right ) ,$
we can use Proposition 40 and find
![]() $Y\in \left [ X_{0}\right ] ^{\omega }$
such that for every
$Y\in \left [ X_{0}\right ] ^{\omega }$
such that for every
![]() $w,z\in \mathbb {W}(S)$
distinct, it is the case that
$w,z\in \mathbb {W}(S)$
distinct, it is the case that
![]() $w\left [ Y\right ] \cap z\left [ Y\right ] $
is finite. We now apply Proposition 43 and get an injective function
$w\left [ Y\right ] \cap z\left [ Y\right ] $
is finite. We now apply Proposition 43 and get an injective function
![]() $h:\omega \longrightarrow Y$
such that
$h:\omega \longrightarrow Y$
such that
![]() $S_{1}=S\cup \left \{ h\right \} $
is a partial cofinitary semigroup base. By the proof of Proposition 46, we know that
$S_{1}=S\cup \left \{ h\right \} $
is a partial cofinitary semigroup base. By the proof of Proposition 46, we know that
![]() $(S_{1},\mathcal {A})$
is a nice pair. It remains to prove that
$(S_{1},\mathcal {A})$
is a nice pair. It remains to prove that
![]() $\mathcal {L(}S_{1},\mathcal {A)\subseteq I}.$
The following claims were proven in Proposition 46:
$\mathcal {L(}S_{1},\mathcal {A)\subseteq I}.$
The following claims were proven in Proposition 46:
Claim 64. Let
![]() $w\in \mathbb {W}\left ( S_{1}\right ) .$
If w contains a subword of the form
$w\in \mathbb {W}\left ( S_{1}\right ) .$
If w contains a subword of the form
![]() $h^{-1}zh$
with
$h^{-1}zh$
with
![]() $z\in \mathbb {W}\left ( S\right ) $
(
$z\in \mathbb {W}\left ( S\right ) $
(
![]() $z\neq Id$
), then img
$z\neq Id$
), then img
![]() $\left ( w\right ) $
is finite.
$\left ( w\right ) $
is finite.
Claim 65. If
![]() $w\in \mathbb {W}\left ( S\right ) $
and
$w\in \mathbb {W}\left ( S\right ) $
and
![]() $A\in \mathcal {A},$
then
$A\in \mathcal {A},$
then
![]() $h^{-1}w\left [ A\right ] $
is finite.
$h^{-1}w\left [ A\right ] $
is finite.
We will now prove that if
![]() $w\in \mathbb {W}\left ( S_{1}\right ) $
and
$w\in \mathbb {W}\left ( S_{1}\right ) $
and
![]() $A\in \mathcal {A},$
then
$A\in \mathcal {A},$
then
![]() $w\left [ A\right ] \in \mathcal {I}.$
We can assume that either h or
$w\left [ A\right ] \in \mathcal {I}.$
We can assume that either h or
![]() $h^{-1}$
appears in
$h^{-1}$
appears in
![]() $w.$
If w does not contain
$w.$
If w does not contain
![]() $h,$
then it most contain some
$h,$
then it most contain some
![]() $h^{-1}.$
In this way, it contains a subword of the form
$h^{-1}.$
In this way, it contains a subword of the form
![]() $h^{-1}z\left [ A\right ] $
(with
$h^{-1}z\left [ A\right ] $
(with
![]() $z\in \mathbb {W}\left ( S\right ) )$
. It follows that
$z\in \mathbb {W}\left ( S\right ) )$
. It follows that
![]() $w\left [ A\right ] $
is finite and we are done. Now, assume that h appears in
$w\left [ A\right ] $
is finite and we are done. Now, assume that h appears in
![]() $w$
. If w contains a word of the form
$w$
. If w contains a word of the form
![]() $h^{-1}zh$
with
$h^{-1}zh$
with
![]() $z\in \mathbb {W}\left ( S\right ) ,$
then img
$z\in \mathbb {W}\left ( S\right ) ,$
then img
![]() $\left ( w\right ) $
is finite and we are done. If this is not the case, we can find
$\left ( w\right ) $
is finite and we are done. If this is not the case, we can find
![]() $z\in \mathbb {W}\left ( S\right ) $
and
$z\in \mathbb {W}\left ( S\right ) $
and
![]() $p\in \mathbb {W}\left ( S_{1}\right ) $
such that
$p\in \mathbb {W}\left ( S_{1}\right ) $
such that
![]() $w=zhp.$
In this case, we have that img
$w=zhp.$
In this case, we have that img
![]() $\left ( w\right ) \subseteq z\left [ Y\right ] $
and we already know that the latter is in
$\left ( w\right ) \subseteq z\left [ Y\right ] $
and we already know that the latter is in
![]() $\mathcal {I}.$
This finishes the proof.
$\mathcal {I}.$
This finishes the proof.
In order to obtain an analogue of Proposition 53, we need to introduce the following notion:
Definition 66. Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\omega .$
We say that
$\omega .$
We say that
![]() $\mathcal {I}$
is cofinitary nice if for every S partial cofinitary semigroup base with
$\mathcal {I}$
is cofinitary nice if for every S partial cofinitary semigroup base with
![]() $\left \vert S\right \vert <\mathfrak {c}$
and
$\left \vert S\right \vert <\mathfrak {c}$
and
![]() $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega },$
there are
$\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega },$
there are
![]() $L\in \left [ \omega \right ] ^{\omega }$
and
$L\in \left [ \omega \right ] ^{\omega }$
and
![]() $\left \{ Y_{n}\mid n\in L\right \} $
with the following properties
$\left \{ Y_{n}\mid n\in L\right \} $
with the following properties
![]() $:$
$:$
-
1.
 $Y_{n}\in \left [ X_{n}\right ] ^{\omega }$
for every
$Y_{n}\in \left [ X_{n}\right ] ^{\omega }$
for every
 $n\in L.$
$n\in L.$
-
2. If
 $w\in \mathbb {W}\left ( S\right ) $
, then
$w\in \mathbb {W}\left ( S\right ) $
, then
 $w[\bigcup \limits _{n\in L}Y_{n}]\in \mathcal {I}.$
$w[\bigcup \limits _{n\in L}Y_{n}]\in \mathcal {I}.$
Note that if
![]() $\mathcal {I}$
is cofinitary nice, then
$\mathcal {I}$
is cofinitary nice, then
![]() $\mathcal {I}$
must be a tall ideal (recall that the identity function belongs to every partial cofinitary semigroup base).
$\mathcal {I}$
must be a tall ideal (recall that the identity function belongs to every partial cofinitary semigroup base).
Proposition 67 (
 $\mathfrak {h=c}$
).
$\mathfrak {h=c}$
).
Let
![]() $\mathcal {I}$
be a cofinitary nice ideal. There is a weakly tight, Katětov maximal MAD family contained in
$\mathcal {I}$
be a cofinitary nice ideal. There is a weakly tight, Katětov maximal MAD family contained in
![]() $\mathcal {I}.$
$\mathcal {I}.$
Proof Fix U and W subsets of
![]() $\mathfrak {c}$
with the following properties:
$\mathfrak {c}$
with the following properties:
-
1.
 $\mathfrak {c}=U\cup W.$
$\mathfrak {c}=U\cup W.$
-
2.
 $U\cap W=\emptyset .$
$U\cap W=\emptyset .$
-
3.
 $\left \vert U\right \vert =\left \vert W\right \vert =\mathfrak {c}.$
$\left \vert U\right \vert =\left \vert W\right \vert =\mathfrak {c}.$
Fix an enumeration
![]() $\left [ \omega \right ] ^{\omega }=\left \{ K_{\alpha } \mid \alpha \in U\right \} $
and
$\left [ \omega \right ] ^{\omega }=\left \{ K_{\alpha } \mid \alpha \in U\right \} $
and
![]() $\left ( \left [ \omega \right ] ^{\omega }\right ) ^{\omega }=\{\overline {U_{\alpha }}\mid \alpha \in W\}$
where
$\left ( \left [ \omega \right ] ^{\omega }\right ) ^{\omega }=\{\overline {U_{\alpha }}\mid \alpha \in W\}$
where
![]() $\overline {U_{\alpha }}=\left \{ U_{\alpha }\left ( n\right ) \mid n\in \omega \right \} .$
We will now recursively define
$\overline {U_{\alpha }}=\left \{ U_{\alpha }\left ( n\right ) \mid n\in \omega \right \} .$
We will now recursively define
![]() $\{\mathcal {A}_{\alpha } \mid \alpha <\mathfrak {c}\}$
and
$\{\mathcal {A}_{\alpha } \mid \alpha <\mathfrak {c}\}$
and
![]() $\{S_{\alpha }\mid \alpha <\mathfrak {c}\}$
such that for every
$\{S_{\alpha }\mid \alpha <\mathfrak {c}\}$
such that for every
![]() $\alpha <\mathfrak {c},$
the following holds:
$\alpha <\mathfrak {c},$
the following holds:
-
1.
 $\mathcal {A}_{0}$
is a partition of
$\mathcal {A}_{0}$
is a partition of
 $\omega $
in countably many pieces and
$\omega $
in countably many pieces and
 $S_{0}=\left \{ Id\right \} .$
$S_{0}=\left \{ Id\right \} .$
-
2.
 $\mathcal {A}_{\alpha }$
is an AD family and
$\mathcal {A}_{\alpha }$
is an AD family and
 $S_{\alpha }$
is a partial cofinitary semigroup base.
$S_{\alpha }$
is a partial cofinitary semigroup base. -
3.
 $(\mathcal {A}_{\alpha },S_{\alpha })$
is a nice pair.
$(\mathcal {A}_{\alpha },S_{\alpha })$
is a nice pair. -
4.
 $\mathcal {L}(\mathcal {A}_{\alpha },S_{\alpha })\subseteq \mathcal {I}.$
$\mathcal {L}(\mathcal {A}_{\alpha },S_{\alpha })\subseteq \mathcal {I}.$
-
5. If
 $\beta <\alpha ,$
then
$\beta <\alpha ,$
then
 $\mathcal {A}_{\beta }\subseteq \mathcal {A} _{\alpha }$
and
$\mathcal {A}_{\beta }\subseteq \mathcal {A} _{\alpha }$
and
 $S_{\beta }\subseteq S_{\alpha }.$
$S_{\beta }\subseteq S_{\alpha }.$
-
6.
 $\left \vert \mathcal {A}_{\alpha }\right \vert +\left \vert S_{\alpha }\right \vert \leq \left \vert \alpha \right \vert +\omega .$
$\left \vert \mathcal {A}_{\alpha }\right \vert +\left \vert S_{\alpha }\right \vert \leq \left \vert \alpha \right \vert +\omega .$
-
7. If
 $\alpha $
is a limit ordinal, then
$\alpha $
is a limit ordinal, then
 $\mathcal {A}_{\alpha } =\bigcup \limits _{\beta <\alpha }\mathcal {A}_{\beta }$
and
$\mathcal {A}_{\alpha } =\bigcup \limits _{\beta <\alpha }\mathcal {A}_{\beta }$
and
 $S_{\alpha } =\bigcup \limits _{\beta <\alpha }S_{\beta }.$
$S_{\alpha } =\bigcup \limits _{\beta <\alpha }S_{\beta }.$
-
8. If
 $\alpha \in W$
and each
$\alpha \in W$
and each
 $U_{\alpha }\left ( n\right ) \in \mathcal {I(L}\left ( S_{\alpha },\mathcal {A}_{\alpha }\right ) \mathcal {)}^{+},$
then there is
$U_{\alpha }\left ( n\right ) \in \mathcal {I(L}\left ( S_{\alpha },\mathcal {A}_{\alpha }\right ) \mathcal {)}^{+},$
then there is
 $A\in \mathcal {A}_{\alpha +1}$
such that
$A\in \mathcal {A}_{\alpha +1}$
such that
 $A\cap U_{\alpha }\left ( n\right ) $
is infinite for infinitely many
$A\cap U_{\alpha }\left ( n\right ) $
is infinite for infinitely many
 $n\in \omega .$
$n\in \omega .$
-
9. If
 $\alpha \in U$
and
$\alpha \in U$
and
 $K_{\alpha }\in \mathcal {I(L(}S_{\alpha } ,\mathcal {A}_{\alpha }\mathcal {))}^{+},$
then there is
$K_{\alpha }\in \mathcal {I(L(}S_{\alpha } ,\mathcal {A}_{\alpha }\mathcal {))}^{+},$
then there is
 $f\in S_{\alpha +1}$
such that
$f\in S_{\alpha +1}$
such that
 $f:\omega \longrightarrow K_{\alpha }.$
$f:\omega \longrightarrow K_{\alpha }.$
Let
![]() $\alpha <\mathfrak {c}$
and assume we have already defined
$\alpha <\mathfrak {c}$
and assume we have already defined
![]() $\{(\mathcal {A} _{\xi },S_{\xi })\mid \xi \leq \alpha \},$
we will now define
$\{(\mathcal {A} _{\xi },S_{\xi })\mid \xi \leq \alpha \},$
we will now define
![]() $\mathcal {A} _{\alpha +1}$
and
$\mathcal {A} _{\alpha +1}$
and
![]() $S_{\alpha +1}$
. There are two cases to consider.
$S_{\alpha +1}$
. There are two cases to consider.
Case 68.
![]() $\alpha \in W.$
$\alpha \in W.$
If there is
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $U_{\alpha }\left ( n\right ) \notin \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+},$
we just define
$U_{\alpha }\left ( n\right ) \notin \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+},$
we just define
![]() $\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }$
and
$\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }$
and
![]() $S_{\alpha +1}=S_{\alpha }.$
Now, assume that
$S_{\alpha +1}=S_{\alpha }.$
Now, assume that
![]() $U_{\alpha }\left ( n\right ) \in \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+}$
for every
$U_{\alpha }\left ( n\right ) \in \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+}$
for every
![]() $n\in \omega .$
Since the size of
$n\in \omega .$
Since the size of
![]() $\mathcal {L}\left ( \mathcal {A} _{\alpha },S_{\alpha }\right ) $
is less than
$\mathcal {L}\left ( \mathcal {A} _{\alpha },S_{\alpha }\right ) $
is less than
![]() $\mathfrak {a=c},$
we can find
$\mathfrak {a=c},$
we can find
![]() $\left \{ X_{n}\mid n\in \omega \right \} $
such that for every
$\left \{ X_{n}\mid n\in \omega \right \} $
such that for every
![]() $n\in \omega ,$
the following holds:
$n\in \omega ,$
the following holds:
-
1.
 $X_{n}\subseteq U_{\alpha }\left ( n\right ) .$
$X_{n}\subseteq U_{\alpha }\left ( n\right ) .$
-
2.
 $X_{n}\in \mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) ^{\perp }.$
$X_{n}\in \mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) ^{\perp }.$
-
3.
 $X_{n}\cap X_{m}=\emptyset $
whenever
$X_{n}\cap X_{m}=\emptyset $
whenever
 $n\neq m.$
$n\neq m.$
Since
![]() $\mathcal {I}$
is cofinitary nice
$\mathcal {I}$
is cofinitary nice
![]() $,$
we can find
$,$
we can find
![]() $L\in \left [ \omega \right ] ^{\omega }$
and
$L\in \left [ \omega \right ] ^{\omega }$
and
![]() $\left \{ Y_{n}\mid n\in L\right \} $
with the following properties:
$\left \{ Y_{n}\mid n\in L\right \} $
with the following properties:
-
1.
 $Y_{n}\in \left [ X_{n}\right ] ^{\omega }$
for each
$Y_{n}\in \left [ X_{n}\right ] ^{\omega }$
for each
 $n\in L.$
$n\in L.$
-
2. If
 $w\in \mathbb {W}\left ( S_{\alpha }\right ) ,$
then
$w\in \mathbb {W}\left ( S_{\alpha }\right ) ,$
then
 $w[\bigcup \limits _{n\in L}Y_{n}]\in \mathcal {I}.$
$w[\bigcup \limits _{n\in L}Y_{n}]\in \mathcal {I}.$
Since both
![]() $\mathcal {A}_{\alpha }$
and
$\mathcal {A}_{\alpha }$
and
![]() $S_{\alpha }$
have size less than
$S_{\alpha }$
have size less than
![]() $\mathfrak {b=c},$
we can apply Proposition 53 and find
$\mathfrak {b=c},$
we can apply Proposition 53 and find
![]() $D\subseteq \bigcup \limits _{n\in L}Y_{n}$
such that D has infinite intersection with all the
$D\subseteq \bigcup \limits _{n\in L}Y_{n}$
such that D has infinite intersection with all the
![]() $Y_{n}$
(
$Y_{n}$
(
![]() $n\in L$
) and
$n\in L$
) and
![]() $(S_{\alpha },\mathcal {A} _{\alpha }\cup \left \{ D\right \} )$
is a nice pair. We now define
$(S_{\alpha },\mathcal {A} _{\alpha }\cup \left \{ D\right \} )$
is a nice pair. We now define
![]() $\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }\cup \left \{ D\right \} $
and
$\mathcal {A}_{\alpha +1}=\mathcal {A}_{\alpha }\cup \left \{ D\right \} $
and
![]() $S_{\alpha +1}=S_{\alpha }.$
$S_{\alpha +1}=S_{\alpha }.$
Case 69.
![]() $\alpha \in U.$
$\alpha \in U.$
If
![]() $K_{\alpha }\notin \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+},$
we just define
$K_{\alpha }\notin \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+},$
we just define
![]() $\mathcal {A}_{\alpha +1} =\mathcal {A}_{\alpha }$
and
$\mathcal {A}_{\alpha +1} =\mathcal {A}_{\alpha }$
and
![]() $S_{\alpha +1}=S_{\alpha }.$
Assume that
$S_{\alpha +1}=S_{\alpha }.$
Assume that
![]() $K_{\alpha }\in \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+}.$
Since the size of
$K_{\alpha }\in \mathcal {I(L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) \mathcal {)}^{+}.$
Since the size of
![]() $\mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) $
is less than
$\mathcal {L}\left ( \mathcal {A}_{\alpha },S_{\alpha }\right ) $
is less than
![]() $\mathfrak {a=c},$
we can find
$\mathfrak {a=c},$
we can find
![]() $X\in \left [ K_{\alpha }\right ] ^{\omega }$
such that
$X\in \left [ K_{\alpha }\right ] ^{\omega }$
such that
![]() $X\in \mathcal {L}\left ( \mathcal {A} _{\alpha },S_{\alpha }\right ) ^{\perp }.$
Moreover, we know that the size of
$X\in \mathcal {L}\left ( \mathcal {A} _{\alpha },S_{\alpha }\right ) ^{\perp }.$
Moreover, we know that the size of
![]() $S_{\alpha }$
is less than
$S_{\alpha }$
is less than
![]() $\mathfrak {h}=\mathfrak {c},$
so by Lemma 63, there is an injective function
$\mathfrak {h}=\mathfrak {c},$
so by Lemma 63, there is an injective function
![]() $f:\omega \longrightarrow X$
such that
$f:\omega \longrightarrow X$
such that
![]() $(S_{\alpha }\cup \left \{ f\right \} ,\mathcal {A}_{\alpha })$
is a nice pair and
$(S_{\alpha }\cup \left \{ f\right \} ,\mathcal {A}_{\alpha })$
is a nice pair and
![]() $\mathcal {L(}S_{\alpha }\cup \left \{ f\right \} ,\mathcal {A}_{\alpha })\subseteq \mathcal {I}$
. Define
$\mathcal {L(}S_{\alpha }\cup \left \{ f\right \} ,\mathcal {A}_{\alpha })\subseteq \mathcal {I}$
. Define
![]() $\mathcal {A} _{\alpha +1}=\mathcal {A}_{\alpha }$
and
$\mathcal {A} _{\alpha +1}=\mathcal {A}_{\alpha }$
and
![]() $S_{\alpha +1}=S_{\alpha }\cup \left \{ f\right \} .$
$S_{\alpha +1}=S_{\alpha }\cup \left \{ f\right \} .$
This finishes the construction. Define
![]() $S_{\mathfrak {c}}=\bigcup \limits _{\alpha <\mathfrak {c}}S_{\alpha }$
and
$S_{\mathfrak {c}}=\bigcup \limits _{\alpha <\mathfrak {c}}S_{\alpha }$
and
![]() $\mathcal {A}_{\mathfrak {c} }=\bigcup \limits _{\alpha <\mathfrak {c}}\mathcal {A}_{\alpha }.$
It is clear that
$\mathcal {A}_{\mathfrak {c} }=\bigcup \limits _{\alpha <\mathfrak {c}}\mathcal {A}_{\alpha }.$
It is clear that
![]() $(S_{\mathfrak {c}},\mathcal {A}_{c})$
is a nice pair. Let
$(S_{\mathfrak {c}},\mathcal {A}_{c})$
is a nice pair. Let
![]() $\mathcal {D=L} (S_{\mathfrak {c}},\mathcal {A}_{c}).$
By Lemma 54, it follows that
$\mathcal {D=L} (S_{\mathfrak {c}},\mathcal {A}_{c}).$
By Lemma 54, it follows that
![]() $\mathcal {D}$
is a Katětov uniform MAD family. It is also clear that
$\mathcal {D}$
is a Katětov uniform MAD family. It is also clear that
![]() $\mathcal {D}$
is weakly tight. By Proposition 30,
$\mathcal {D}$
is weakly tight. By Proposition 30,
![]() $\mathcal {D}$
is a Katětov maximal MAD family contained in
$\mathcal {D}$
is a Katětov maximal MAD family contained in
![]() $\mathcal {I}.$
$\mathcal {I}.$
The Definition 66 is exactly what is needed in order to obtain Proposition 67. In practice, it is common to find an stronger property:
Definition 70. Let W be a countable set and
![]() $\mathcal {I}$
a tall ideal on
$\mathcal {I}$
a tall ideal on
![]() $W.$
$W.$
-
1. Define Inj
 $\left ( W\right ) $
as the set of all injective
$\left ( W\right ) $
as the set of all injective
 $g:A\longrightarrow W$
with
$g:A\longrightarrow W$
with
 $A\subseteq W.$
$A\subseteq W.$
-
2. We say that
 $\mathcal {I}$
is injectively nice if for every
$\mathcal {I}$
is injectively nice if for every
 $S\subseteq $
Inj
$S\subseteq $
Inj
 $\left ( W\right ) $
with
$\left ( W\right ) $
with
 $\left \vert S\right \vert <\mathfrak {c}$
and
$\left \vert S\right \vert <\mathfrak {c}$
and
 $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ W\right ] ^{\omega },$
there are
$\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ W\right ] ^{\omega },$
there are
 $L\in \left [ \omega \right ] ^{\omega }$
and
$L\in \left [ \omega \right ] ^{\omega }$
and
 $\left \{ Y_{n}\mid n\in L\right \} $
such that
$\left \{ Y_{n}\mid n\in L\right \} $
such that
 $:$
$:$
-
(a)
 $Y_{n}\in \left [ X_{n}\right ] ^{\omega }$
for every
$Y_{n}\in \left [ X_{n}\right ] ^{\omega }$
for every
 $n\in L.$
$n\in L.$
-
(b) If
 $f\in S,$
then
$f\in S,$
then
 $f[\bigcup \limits _{n\in L}Y_{n}]\in \mathcal {I}.$
$f[\bigcup \limits _{n\in L}Y_{n}]\in \mathcal {I}.$
-
This definition and Definition 66 are almost exactly the same, except that now we do not require a partial cofinitary semigroup base, only a set of injective partial functions.
We will now start proving that (consistently) there may be a Katětov maximal MAD family that is destructible by Sacks forcing. In order to do so, we will prove that it is consistent that tr(ctble) is injectively nice. We start with some definitions:
Definition 71. Let
![]() $A\subseteq 2^{<\omega }.$
$A\subseteq 2^{<\omega }.$
-
1. Let
 $f\in 2^{\omega }.$
Define
$f\in 2^{\omega }.$
Define
 $\widehat {f}=\left \{ f\upharpoonright n\mid n\in \omega \right \} .$
$\widehat {f}=\left \{ f\upharpoonright n\mid n\in \omega \right \} .$
-
2. Let
 $f,g\in 2^{\leq \omega }.$
Define
$f,g\in 2^{\leq \omega }.$
Define
 $\triangle \left ( f,g\right ) = \mathrm{min} \left \{ n\mid f\left ( n\right ) \neq g\left ( n\right ) \right \} .$
$\triangle \left ( f,g\right ) = \mathrm{min} \left \{ n\mid f\left ( n\right ) \neq g\left ( n\right ) \right \} .$
-
3. A is a branch-set if there is
 $r\in 2^{\omega }$
such that
$r\in 2^{\omega }$
such that
 $A\subseteq \widehat {r}.$
$A\subseteq \widehat {r}.$
-
4. A is an almost branch-set if there is
 $F\in \left [ A\right ] ^{<\omega }$
such that
$F\in \left [ A\right ] ^{<\omega }$
such that
 $A\setminus F$
is a branch set.
$A\setminus F$
is a branch set. -
5. We say that A is a comb if A is an infinite antichain and there is
 $r\in 2^{\omega }$
such that for every
$r\in 2^{\omega }$
such that for every
 $s,t\in A,$
if
$s,t\in A,$
if
 $s\neq t,$
then
$s\neq t,$
then
 $\triangle \left ( s,r\right ) \neq \triangle \left ( t,r\right ) .$
In this situation, we say that A is a comb with base
$\triangle \left ( s,r\right ) \neq \triangle \left ( t,r\right ) .$
In this situation, we say that A is a comb with base
 $r.$
$r.$
-
6. A is almost a comb if there is
 $F\in \left [ A\right ] ^{<\omega }$
such that
$F\in \left [ A\right ] ^{<\omega }$
such that
 $A\setminus F$
is a comb. In the same way, A is almost a comb with base r if there is
$A\setminus F$
is a comb. In the same way, A is almost a comb with base r if there is
 $F\in \left [ A\right ] ^{<\omega }$
such that
$F\in \left [ A\right ] ^{<\omega }$
such that
 $A\setminus F$
is a comb with base
$A\setminus F$
is a comb with base
 $r.$
$r.$
It is easy to see that a (almost) comb has a unique base. Note that every almost branch-set and every almost comb is in tr(ctble).
Lemma 72. Every infinite subset of
![]() $2^{<\omega }$
contains an infinite branch-set or a comb.
$2^{<\omega }$
contains an infinite branch-set or a comb.
Proof By Ramsey’s Theorem, every infinite subset of
![]() $2^{<\omega }$
contains an infinite branch-set or an infinite antichain. In this way, it is enough to prove that if
$2^{<\omega }$
contains an infinite branch-set or an infinite antichain. In this way, it is enough to prove that if
![]() $B\subseteq 2^{<\omega }$
is an infinite antichain, then B contains a comb. For every
$B\subseteq 2^{<\omega }$
is an infinite antichain, then B contains a comb. For every
![]() $s\in B,$
define
$s\in B,$
define
![]() $f_{s}\in 2^{\omega }$
given by
$f_{s}\in 2^{\omega }$
given by
![]() $f_{s}=s^{\frown }\overline {0}$
(where
$f_{s}=s^{\frown }\overline {0}$
(where
![]() $\overline {0}$
is the constant
$\overline {0}$
is the constant
![]() $0$
sequence and
$0$
sequence and
![]() $^{\frown }$
denotes concatenation). Since
$^{\frown }$
denotes concatenation). Since
![]() $2^{\omega }$
is compact, we can find
$2^{\omega }$
is compact, we can find
![]() $C\in \left [ B\right ] ^{\omega }$
and
$C\in \left [ B\right ] ^{\omega }$
and
![]() $r\in 2^{\omega }$
such that C converges to
$r\in 2^{\omega }$
such that C converges to
![]() $r.$
It is easy to see that C contains a comb with base
$r.$
It is easy to see that C contains a comb with base
![]() $r.$
$r.$
Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\omega .$
Recall that an ideal
$\omega .$
Recall that an ideal
![]() $\mathcal {I}$
is
$\mathcal {I}$
is
![]() $\omega $
-hitting if for every
$\omega $
-hitting if for every
![]() $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega },$
there is
$\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega },$
there is
![]() $A\in \mathcal {I}$
such that
$A\in \mathcal {I}$
such that
![]() $A\cap X_{n}$
is infinite for all
$A\cap X_{n}$
is infinite for all
![]() $n\in \omega .$
The class of
$n\in \omega .$
The class of
![]() $\omega \,$
-hitting ideals has been extensively studied in the past and has many applications (see [Reference Brendle and Hrušák7, Reference Chodounský, González and Hrušák15, Reference Dow17, Reference Hrušák39, Reference Hrušák and Minami41, Reference Hrušák and Ramos-García42, Reference Michael, Meza-Alcántara, Thümmel and Uzcátegui55]). It is easy to see that tr(ctble) is not
$\omega \,$
-hitting ideals has been extensively studied in the past and has many applications (see [Reference Brendle and Hrušák7, Reference Chodounský, González and Hrušák15, Reference Dow17, Reference Hrušák39, Reference Hrušák and Minami41, Reference Hrušák and Ramos-García42, Reference Michael, Meza-Alcántara, Thümmel and Uzcátegui55]). It is easy to see that tr(ctble) is not
![]() $\omega $
-hitting: If
$\omega $
-hitting: If
![]() $D\subseteq 2^{\omega }$
is any countable dense set, then the family
$D\subseteq 2^{\omega }$
is any countable dense set, then the family
![]() $\{\widehat {d}\mid d\in D\}$
witnesses that tr(ctble) is not
$\{\widehat {d}\mid d\in D\}$
witnesses that tr(ctble) is not
![]() $\omega $
-hitting. However, we will see that it satisfies a weaker property.
$\omega $
-hitting. However, we will see that it satisfies a weaker property.
Definition 73. Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\omega .$
We say that
$\omega .$
We say that
![]() $\mathcal {I}$
is weakly
$\mathcal {I}$
is weakly
![]() $\omega $
-hitting, if for every
$\omega $
-hitting, if for every
![]() $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega },$
there is
$\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega },$
there is
![]() $A\in \mathcal {I}$
such that
$A\in \mathcal {I}$
such that
![]() $A\cap X_{n}$
is infinite for infinitely many
$A\cap X_{n}$
is infinite for infinitely many
![]() $n\in \omega .$
$n\in \omega .$
The following lemma will be helpful:
Lemma 74. Let
![]() $\left \{ A_{n}\mid n\in \omega \right \} $
be a family of antichains of
$\left \{ A_{n}\mid n\in \omega \right \} $
be a family of antichains of
![]() $2^{<\omega }, r\in 2^{\omega }$
and
$2^{<\omega }, r\in 2^{\omega }$
and
![]() $\left \{ r_{n}\mid n\in \omega \right \} \subseteq 2^{\omega }$
such that for every
$\left \{ r_{n}\mid n\in \omega \right \} \subseteq 2^{\omega }$
such that for every
![]() $n\in \omega ,$
the following holds
$n\in \omega ,$
the following holds
![]() $:$
$:$
-
1.
 $A_{n}$
is a comb with base
$A_{n}$
is a comb with base
 $r_{n}.$
$r_{n}.$
-
2. The sequence
 $\left \langle r_{n}\right \rangle _{n\in \omega }$
converges to
$\left \langle r_{n}\right \rangle _{n\in \omega }$
converges to
 $r.$
$r.$
-
3.
 $r\neq r_{n}.$
$r\neq r_{n}.$
-
4. If
 $s\in A_{n},$
then
$s\in A_{n},$
then
 $\triangle \left ( s,r_{n}\right )>\triangle \left ( s,r\right ) .$
$\triangle \left ( s,r_{n}\right )>\triangle \left ( s,r\right ) .$
Then
![]() $\pi (\bigcup \limits _{n\in \omega }A_{n})=\emptyset .$
In particular,
$\pi (\bigcup \limits _{n\in \omega }A_{n})=\emptyset .$
In particular,
![]() $\bigcup \limits _{n\in \omega }A_{n}\in $
tr(ctble).
$\bigcup \limits _{n\in \omega }A_{n}\in $
tr(ctble).
Proof Let
![]() $B=\bigcup \limits _{n\in \omega }A_{n}$
and note that
$B=\bigcup \limits _{n\in \omega }A_{n}$
and note that
![]() $\widehat {r}\cap B=\emptyset ,$
so
$\widehat {r}\cap B=\emptyset ,$
so
![]() $r\notin \pi (B).$
Pick
$r\notin \pi (B).$
Pick
![]() $x\in 2^{\omega },$
we need to prove that
$x\in 2^{\omega },$
we need to prove that
![]() $x\notin \pi \left ( B\right ) .$
We can already assume that
$x\notin \pi \left ( B\right ) .$
We can already assume that
![]() $x\neq r.$
Since each
$x\neq r.$
Since each
![]() $A_{i}$
is an antichain, it follows that
$A_{i}$
is an antichain, it follows that
![]() $\widehat {x}\cap A_{i}$
is finite. In order to prove that
$\widehat {x}\cap A_{i}$
is finite. In order to prove that
![]() $x\notin \pi \left ( B\right ) ,$
it is enough to prove that there are only finitely many
$x\notin \pi \left ( B\right ) ,$
it is enough to prove that there are only finitely many
![]() $n\in \omega $
for which
$n\in \omega $
for which
![]() $\widehat {x}\cap A_{n}\neq \emptyset .$
$\widehat {x}\cap A_{n}\neq \emptyset .$
Let
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $\widehat {x}\cap A_{n}\neq \emptyset $
and define
$\widehat {x}\cap A_{n}\neq \emptyset $
and define
![]() $k=\triangle \left ( x,r\right ) .$
Choose any
$k=\triangle \left ( x,r\right ) .$
Choose any
![]() $s\in \widehat {x}\cap A_{n}.$
Since
$s\in \widehat {x}\cap A_{n}.$
Since
![]() $s\notin \widehat {r},$
it follows that
$s\notin \widehat {r},$
it follows that
 $ \begin {array} [c]{ccc} k & = & \triangle \left ( x,r\right ) \\ & = & \triangle \left ( s,r\right ) \\ & < & \triangle \left ( s,r_{n}\right ). \end {array} $
$ \begin {array} [c]{ccc} k & = & \triangle \left ( x,r\right ) \\ & = & \triangle \left ( s,r\right ) \\ & < & \triangle \left ( s,r_{n}\right ). \end {array} $
Hence
![]() $\triangle \left ( r,r_{n}\right ) =k.$
Since
$\triangle \left ( r,r_{n}\right ) =k.$
Since
![]() $\left \langle r_{i}\right \rangle _{i\in \omega }$
converges to
$\left \langle r_{i}\right \rangle _{i\in \omega }$
converges to
![]() $r,$
it follows that there are only finitely many possibilities for
$r,$
it follows that there are only finitely many possibilities for
![]() $n.$
$n.$
The following is a similar lemma:
Lemma 75. Let
![]() $\left \{ A_{n}\mid n\in \omega \right \} $
be a set of antichains of
$\left \{ A_{n}\mid n\in \omega \right \} $
be a set of antichains of
![]() $2^{<\omega }$
and
$2^{<\omega }$
and
![]() $r\in 2^{\omega }$
such that each
$r\in 2^{\omega }$
such that each
![]() $A_{n}$
is a comb with base
$A_{n}$
is a comb with base
![]() $r.$
If for every
$r.$
If for every
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $s\in A_{n}$
we have that
$s\in A_{n}$
we have that
![]() $\triangle \left ( s,r\right )>n,$
then
$\triangle \left ( s,r\right )>n,$
then
![]() $\pi (\bigcup \limits _{n\in \omega }A_{n})=\emptyset $
(so
$\pi (\bigcup \limits _{n\in \omega }A_{n})=\emptyset $
(so
![]() $\bigcup \limits _{n\in \omega }A_{n}\in $
tr(ctble)).
$\bigcup \limits _{n\in \omega }A_{n}\in $
tr(ctble)).
Proof Let
![]() $B=\bigcup \limits _{n\in \omega }A_{n}$
. As before,
$B=\bigcup \limits _{n\in \omega }A_{n}$
. As before,
![]() $\widehat {r}\cap B=\emptyset ,$
so
$\widehat {r}\cap B=\emptyset ,$
so
![]() $r\notin \pi (B).$
Let
$r\notin \pi (B).$
Let
![]() $x\in 2^{\omega },$
we need to prove that
$x\in 2^{\omega },$
we need to prove that
![]() $x\notin \pi \left ( B\right ) .$
As in the lemma before, we can already assume that
$x\notin \pi \left ( B\right ) .$
As in the lemma before, we can already assume that
![]() $x\neq r$
and it is enough to prove that there are only finitely many
$x\neq r$
and it is enough to prove that there are only finitely many
![]() $n\in \omega $
for which
$n\in \omega $
for which
![]() $\widehat {x}\cap A_{n}\neq \emptyset .$
$\widehat {x}\cap A_{n}\neq \emptyset .$
Let
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $\widehat {x}\cap A_{n}\neq \emptyset $
and define
$\widehat {x}\cap A_{n}\neq \emptyset $
and define
![]() $k=\triangle \left ( x,r\right ) .$
By our hypothesis, we conclude that
$k=\triangle \left ( x,r\right ) .$
By our hypothesis, we conclude that
![]() $n<k.$
Therefore, there are only finitely many possibilities for
$n<k.$
Therefore, there are only finitely many possibilities for
![]() $n.$
$n.$
With this results we can prove the following proposition. Strictly speaking, it will not be needed in the rest of the paper, but it is a good warm-up for the following arguments.
Proposition 76. The ideal tr(ctble) is weakly
![]() $\omega $
-hitting.
$\omega $
-hitting.
Proof Let
![]() $\mathcal {A}=\left \{ A_{n}\mid n\in \omega \right \} \subseteq \left [ 2^{<\omega }\right ] ^{\omega }.$
By shrinking each
$\mathcal {A}=\left \{ A_{n}\mid n\in \omega \right \} \subseteq \left [ 2^{<\omega }\right ] ^{\omega }.$
By shrinking each
![]() $A_{n}$
and passing to an infinite subset of
$A_{n}$
and passing to an infinite subset of
![]() $\mathcal {A}$
, we may assume that either every
$\mathcal {A}$
, we may assume that either every
![]() $A_{n}$
is a branch-set or every
$A_{n}$
is a branch-set or every
![]() $A_{n}$
is a comb (see Lemma 72). We divide the proof by cases:
$A_{n}$
is a comb (see Lemma 72). We divide the proof by cases:
Case 77. Each
![]() $A_{n}$
is a branch-set.
$A_{n}$
is a branch-set.
For every
![]() $n\in \omega ,$
let
$n\in \omega ,$
let
![]() $r_{n}\in 2^{\omega }$
such that
$r_{n}\in 2^{\omega }$
such that
![]() $A_{n}\subseteq \widehat {r}_{n}.$
If there is
$A_{n}\subseteq \widehat {r}_{n}.$
If there is
![]() $r\in 2^{\omega }$
such that there are infinitely many
$r\in 2^{\omega }$
such that there are infinitely many
![]() $n\in \omega $
for which
$n\in \omega $
for which
![]() $r=r_{n},$
then
$r=r_{n},$
then
![]() $\widehat {r}$
intersects infinitely many elements of
$\widehat {r}$
intersects infinitely many elements of
![]() $\mathcal {A}.$
Assume this is not the case. Since
$\mathcal {A}.$
Assume this is not the case. Since
![]() $2^{\omega }$
is compact, we can find
$2^{\omega }$
is compact, we can find
![]() $W\in \left [ \omega \right ] ^{\omega }$
such that
$W\in \left [ \omega \right ] ^{\omega }$
such that
![]() $\left \{ r_{n}\mid n\in W\right \} $
is a converging sequence. Let
$\left \{ r_{n}\mid n\in W\right \} $
is a converging sequence. Let
![]() $B=\bigcup \limits _{n\in W}\widehat {r}_{n}.$
It is clear that
$B=\bigcup \limits _{n\in W}\widehat {r}_{n}.$
It is clear that
![]() $\pi \left ( B\right ) $
is countable, so
$\pi \left ( B\right ) $
is countable, so
![]() $B\in $
tr(ctble) and B has infinite intersection with infinitely many elements of
$B\in $
tr(ctble) and B has infinite intersection with infinitely many elements of
![]() $\mathcal {A}.$
$\mathcal {A}.$
Case 78. Each
![]() $A_{n}$
is a comb.
$A_{n}$
is a comb.
For every
![]() $n\in \omega ,$
let
$n\in \omega ,$
let
![]() $r_{n}\in 2^{\omega }$
such that
$r_{n}\in 2^{\omega }$
such that
![]() $A_{n}$
is a comb with base
$A_{n}$
is a comb with base
![]() $r_{n}.$
First consider the case where there is
$r_{n}.$
First consider the case where there is
![]() $r\in 2^{\omega }$
such that there are infinitely many
$r\in 2^{\omega }$
such that there are infinitely many
![]() $n\in \omega $
for which
$n\in \omega $
for which
![]() $r=r_{n}.$
Let
$r=r_{n}.$
Let
![]() $W=\left \{ n\in \omega \mid r_{n}=r\right \} .$
For every
$W=\left \{ n\in \omega \mid r_{n}=r\right \} .$
For every
![]() $n\in \omega ,$
we can find
$n\in \omega ,$
we can find
![]() $B_{n}\in \left [ A_{n}\right ] ^{\omega }$
such that for every
$B_{n}\in \left [ A_{n}\right ] ^{\omega }$
such that for every
![]() $s\in B_{n},$
we have that
$s\in B_{n},$
we have that
![]() $\triangle \left ( s,r\right )>n.$
By Lemma 75, it follows that
$\triangle \left ( s,r\right )>n.$
By Lemma 75, it follows that
![]() $\bigcup \limits _{n\in W}B_{n}\in $
tr(ctble) and we are done.
$\bigcup \limits _{n\in W}B_{n}\in $
tr(ctble) and we are done.
Now assume there is no such
![]() $r.$
Since
$r.$
Since
![]() $2^{\omega }$
is compact, we can find
$2^{\omega }$
is compact, we can find
![]() $y\in 2^{\omega }$
and
$y\in 2^{\omega }$
and
![]() $Z\in \left [ \omega \right ] ^{\omega }$
such that
$Z\in \left [ \omega \right ] ^{\omega }$
such that
![]() $\left \{ r_{n}\mid n\in Z\right \} $
converges to y and
$\left \{ r_{n}\mid n\in Z\right \} $
converges to y and
![]() $y\neq r_{n}$
for every
$y\neq r_{n}$
for every
![]() $n\in Z.$
We can now find
$n\in Z.$
We can now find
![]() $B_{n}\in \left [ A_{n}\right ] ^{\omega }$
(for
$B_{n}\in \left [ A_{n}\right ] ^{\omega }$
(for
![]() $n\in Z$
) such that for every
$n\in Z$
) such that for every
![]() $s\in B,$
it is the case that
$s\in B,$
it is the case that
![]() $\triangle \left ( s,r_{n}\right )>\triangle \left ( s,r\right ) .$
By Lemma 74, we know that
$\triangle \left ( s,r_{n}\right )>\triangle \left ( s,r\right ) .$
By Lemma 74, we know that
![]() $\bigcup \limits _{n\in Z}B_{n}\in $
tr(ctble) and we are done.
$\bigcup \limits _{n\in Z}B_{n}\in $
tr(ctble) and we are done.
We will now prove that tr(ctble) may be injectively nice:
Proposition 79 (
 $\mathfrak {h=c}$
).
$\mathfrak {h=c}$
).
tr(ctble) is injectively nice.
Proof Let
![]() $S\subseteq $
Inj
$S\subseteq $
Inj
![]() $\left ( 2^{<\omega }\right ) $
of size less that
$\left ( 2^{<\omega }\right ) $
of size less that
![]() $\mathfrak {c}$
and
$\mathfrak {c}$
and
![]() $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ 2^{<\omega }\right ] ^{\omega }.$
Since
$\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ 2^{<\omega }\right ] ^{\omega }.$
Since
![]() $\left \vert S\right \vert <\mathfrak {h}$
and with the aid of Lemma 72, we can find
$\left \vert S\right \vert <\mathfrak {h}$
and with the aid of Lemma 72, we can find
![]() $\left \{ Z_{n}\mid n\in \omega \right \} $
with the following properties:
$\left \{ Z_{n}\mid n\in \omega \right \} $
with the following properties:
-
1.
 $Z_{n}\in \left [ X_{n}\right ] ^{\omega }$
for every
$Z_{n}\in \left [ X_{n}\right ] ^{\omega }$
for every
 $n\in \omega .$
$n\in \omega .$
-
2. If
 $w\in S$
and
$w\in S$
and
 $n\in \omega ,$
then
$n\in \omega ,$
then
 $w\left [ Z_{n}\right ] $
is an almost branch-set or an almost comb.
$w\left [ Z_{n}\right ] $
is an almost branch-set or an almost comb.
Let
![]() $w\in S,$
define the following sets:
$w\in S,$
define the following sets:
-
1.
 $D_{0}\left ( w\right ) $
is the set of all
$D_{0}\left ( w\right ) $
is the set of all
 $E\in \left [ \omega \right ] ^{\omega }$
for which there are
$E\in \left [ \omega \right ] ^{\omega }$
for which there are
 $r\in 2^{\omega }, n\in \omega $
and
$r\in 2^{\omega }, n\in \omega $
and
 $\left \{ r_{i}\mid i\in E\wedge i>n\right \} \subseteq 2^{\omega }$
such that for every
$\left \{ r_{i}\mid i\in E\wedge i>n\right \} \subseteq 2^{\omega }$
such that for every
 $i,j\in E$
with
$i,j\in E$
with
 $n<i,j,$
the following conditions hold:
$n<i,j,$
the following conditions hold:-
(a)
 $w\left [ Z_{i}\right ] $
is an almost comb with base
$w\left [ Z_{i}\right ] $
is an almost comb with base
 $r_{i}.$
$r_{i}.$
-
(b)
 $r_{i}\neq r.$
$r_{i}\neq r.$
-
(c) If
 $i\neq j,$
then
$i\neq j,$
then
 $r_{i}\neq r_{j}.$
$r_{i}\neq r_{j}.$
-
(d)
 $\left \{ r_{l}\mid l\in E\wedge l>n\right \} $
converges to
$\left \{ r_{l}\mid l\in E\wedge l>n\right \} $
converges to
 $r.$
$r.$
-
-
2.
 $D_{1}\left ( w\right ) $
is the set of all
$D_{1}\left ( w\right ) $
is the set of all
 $E\in \left [ \omega \right ] ^{\omega }$
for which there are
$E\in \left [ \omega \right ] ^{\omega }$
for which there are
 $r\in 2^{\omega }$
and
$r\in 2^{\omega }$
and
 $n\in \omega $
such that if
$n\in \omega $
such that if
 $i\in E$
and
$i\in E$
and
 $i>n,$
then
$i>n,$
then
 $w\left [ Z_{i}\right ] $
is an almost comb with base
$w\left [ Z_{i}\right ] $
is an almost comb with base
 $r.$
$r.$
-
3.
 $D_{2}\left ( w\right ) $
is the set of all
$D_{2}\left ( w\right ) $
is the set of all
 $E\in \left [ \omega \right ] ^{\omega }$
for which there are
$E\in \left [ \omega \right ] ^{\omega }$
for which there are
 $d\in 2^{\omega }$
and
$d\in 2^{\omega }$
and
 $n\in \omega $
such that if
$n\in \omega $
such that if
 $i\in E$
and
$i\in E$
and
 $i>n,$
then
$i>n,$
then
 $w\left [ Z_{i}\right ] \subseteq ^{\ast }\widehat {d}.$
$w\left [ Z_{i}\right ] \subseteq ^{\ast }\widehat {d}.$
-
4.
 $D_{3}\left ( w\right ) $
is the set of all
$D_{3}\left ( w\right ) $
is the set of all
 $E\in \left [ \omega \right ] ^{\omega }$
for which there are
$E\in \left [ \omega \right ] ^{\omega }$
for which there are
 $d\in 2^{\omega }, n\in \omega $
and
$d\in 2^{\omega }, n\in \omega $
and
 $\left \{ d_{i}\mid i\in E\wedge i>n\right \} \subseteq 2^{\omega }$
such that for every
$\left \{ d_{i}\mid i\in E\wedge i>n\right \} \subseteq 2^{\omega }$
such that for every
 $i,j\in E$
with
$i,j\in E$
with
 $n<i,j,$
the following conditions hold:
$n<i,j,$
the following conditions hold:-
(a)
 $w\left [ Z_{i}\right ] \subseteq ^{\ast }\widehat {d}_{i}.$
$w\left [ Z_{i}\right ] \subseteq ^{\ast }\widehat {d}_{i}.$
-
(b)
 $d_{i}\neq d.$
$d_{i}\neq d.$
-
(c) If
 $i\neq j,$
then
$i\neq j,$
then
 $d_{i}\neq d_{j}.$
$d_{i}\neq d_{j}.$
-
(d)
 $\left \{ d_{l}\mid l\in E\wedge l>n\right \} $
converges to
$\left \{ d_{l}\mid l\in E\wedge l>n\right \} $
converges to
 $d.$
$d.$
-
It follows that each
![]() $D_{i}\left ( w\right ) $
is open in
$D_{i}\left ( w\right ) $
is open in
![]() $\left [ \omega \right ] ^{\omega }$
(for
$\left [ \omega \right ] ^{\omega }$
(for
![]() $i<4$
) and
$i<4$
) and
![]() $D\left ( w\right ) =\bigcup \limits _{i<4}D_{i}\left ( w\right ) $
is an open dense subset of
$D\left ( w\right ) =\bigcup \limits _{i<4}D_{i}\left ( w\right ) $
is an open dense subset of
![]() $\left [ \omega \right ] ^{\omega }.$
Now, since
$\left [ \omega \right ] ^{\omega }.$
Now, since
![]() $\left \vert S\right \vert <\mathfrak {h},$
we can find
$\left \vert S\right \vert <\mathfrak {h},$
we can find
![]() $L\in \bigcap \limits _{w\in S}D\left ( w\right ) .$
For every
$L\in \bigcap \limits _{w\in S}D\left ( w\right ) .$
For every
![]() $w\in S,$
we will define a function
$w\in S,$
we will define a function
![]() $f_{w}:L\longrightarrow \left [ 2^{<\omega }\right ] ^{<\omega }$
as follows:
$f_{w}:L\longrightarrow \left [ 2^{<\omega }\right ] ^{<\omega }$
as follows:
Case 80.
![]() $L\in D_{0}\left ( w\right ) .$
$L\in D_{0}\left ( w\right ) .$
Let
![]() $r\in 2^{\omega }, n\in \omega $
and
$r\in 2^{\omega }, n\in \omega $
and
![]() $\left \{ r_{i}\mid i\in L\wedge i>n\right \} \subseteq 2^{\omega }$
witnessing that
$\left \{ r_{i}\mid i\in L\wedge i>n\right \} \subseteq 2^{\omega }$
witnessing that
![]() $L\in D_{0}\left ( w\right ) .$
Pick
$L\in D_{0}\left ( w\right ) .$
Pick
![]() $m\in L.$
$m\in L.$
-
1. If
 $m\leq n,$
then
$m\leq n,$
then
 $f_{w}\left ( m\right ) =\emptyset .$
$f_{w}\left ( m\right ) =\emptyset .$
-
2. If
 $m>n,$
then
$m>n,$
then
 $f_{w}\left ( m\right ) $
has the following properties:
$f_{w}\left ( m\right ) $
has the following properties:-
(a)
 $w\left [ Z_{m}\setminus f_{w}\left ( m\right ) \right ] $
is a comb with base
$w\left [ Z_{m}\setminus f_{w}\left ( m\right ) \right ] $
is a comb with base
 $r_{m}.$
$r_{m}.$
-
(b) If
 $s\in Z_{m}\setminus f_{w}\left ( m\right ) ,$
then
$s\in Z_{m}\setminus f_{w}\left ( m\right ) ,$
then
 $\triangle \left ( w\left ( s\right ) ,r_{m}\right )>\triangle \left ( w\left ( s\right ) ,r\right ) .$
$\triangle \left ( w\left ( s\right ) ,r_{m}\right )>\triangle \left ( w\left ( s\right ) ,r\right ) .$
-
Case 81.
![]() $L\in D_{1}\left ( w\right ) .$
$L\in D_{1}\left ( w\right ) .$
Let
![]() $r\in 2^{\omega }$
and
$r\in 2^{\omega }$
and
![]() $n\in \omega $
witnessing that
$n\in \omega $
witnessing that
![]() $L\in D_{1}\left ( w\right ) .$
Pick
$L\in D_{1}\left ( w\right ) .$
Pick
![]() $m\in L.$
$m\in L.$
-
1. If
 $m\leq n,$
then
$m\leq n,$
then
 $f_{w}\left ( m\right ) =\emptyset .$
$f_{w}\left ( m\right ) =\emptyset .$
-
2. If
 $m>n,$
then
$m>n,$
then
 $f_{w}\left ( m\right ) $
has the following properties:
$f_{w}\left ( m\right ) $
has the following properties:-
(a)
 $w\left [ Z_{m}\setminus f_{w}\left ( m\right ) \right ] $
is a comb with base
$w\left [ Z_{m}\setminus f_{w}\left ( m\right ) \right ] $
is a comb with base
 $r.$
$r.$
-
(b) If
 $s\in Z_{m}\setminus f_{w}\left ( m\right ) ,$
then
$s\in Z_{m}\setminus f_{w}\left ( m\right ) ,$
then
 $\triangle \left ( w\left ( s\right ) ,r\right )>m.$
$\triangle \left ( w\left ( s\right ) ,r\right )>m.$
-
Case 82.
![]() $L\in D_{2}\left ( w\right ) .$
$L\in D_{2}\left ( w\right ) .$
Let
![]() $d\in 2^{\omega }$
and
$d\in 2^{\omega }$
and
![]() $n\in \omega $
witnessing that
$n\in \omega $
witnessing that
![]() $L\in D_{2}\left ( w\right ) .$
Pick
$L\in D_{2}\left ( w\right ) .$
Pick
![]() $m\in L.$
$m\in L.$
-
1. If
 $m\leq n,$
then
$m\leq n,$
then
 $f_{w}\left ( m\right ) =\emptyset .$
$f_{w}\left ( m\right ) =\emptyset .$
-
2. If
 $m>n,$
then
$m>n,$
then
 $f_{w}\left ( m\right ) $
is such that
$f_{w}\left ( m\right ) $
is such that
 $w\left [ Z_{m}\setminus f_{w}\left ( m\right ) \right ] \subseteq \widehat {d}.$
$w\left [ Z_{m}\setminus f_{w}\left ( m\right ) \right ] \subseteq \widehat {d}.$
Case 83.
![]() $L\in D_{3}\left ( w\right ) .$
$L\in D_{3}\left ( w\right ) .$
Let
![]() $d\in 2^{\omega }, n\in \omega $
and
$d\in 2^{\omega }, n\in \omega $
and
![]() $\left \{ d_{i}\mid i\in E\wedge i>n\right \} \subseteq 2^{\omega }$
witnessing that
$\left \{ d_{i}\mid i\in E\wedge i>n\right \} \subseteq 2^{\omega }$
witnessing that
![]() $L\in D_{3}\left ( w\right ) .$
Pick
$L\in D_{3}\left ( w\right ) .$
Pick
![]() $m\in L.$
$m\in L.$
-
1. If
 $m\leq n,$
then
$m\leq n,$
then
 $f_{w}\left ( m\right ) =\emptyset .$
$f_{w}\left ( m\right ) =\emptyset .$
-
2. If
 $m>n,$
then
$m>n,$
then
 $f_{w}\left ( m\right ) $
has the following properties:
$f_{w}\left ( m\right ) $
has the following properties:-
(a)
 $w\left [ Z_{m}\setminus f_{w}\left ( m\right ) \right ] \subseteq \widehat {d}_{m}.$
$w\left [ Z_{m}\setminus f_{w}\left ( m\right ) \right ] \subseteq \widehat {d}_{m}.$
-
(b) If
 $s\in Z_{m}\setminus f_{w}\left ( m\right ) ,$
then
$s\in Z_{m}\setminus f_{w}\left ( m\right ) ,$
then
 $\triangle \left ( w\left ( s\right ) ,d\right ) =\triangle \left ( d,d_{m}\right ) .$
$\triangle \left ( w\left ( s\right ) ,d\right ) =\triangle \left ( d,d_{m}\right ) .$
-
Since
![]() $\left \vert S\right \vert <\mathfrak {b},$
we can find a function
$\left \vert S\right \vert <\mathfrak {b},$
we can find a function
![]() $g:L\longrightarrow \left [ 2^{<\omega }\right ] ^{<\omega }$
such that for every
$g:L\longrightarrow \left [ 2^{<\omega }\right ] ^{<\omega }$
such that for every
![]() $w\in S,$
it is the case that
$w\in S,$
it is the case that
![]() $f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $
for almost all
$f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $
for almost all
![]() $m\in L.$
Given
$m\in L.$
Given
![]() $m\in L,$
define
$m\in L,$
define
![]() $Y_{m} =Z_{m}\setminus g\left ( m\right ) .$
We claim that this are the items we were looking for. We need to prove that if
$Y_{m} =Z_{m}\setminus g\left ( m\right ) .$
We claim that this are the items we were looking for. We need to prove that if
![]() $w\in S,$
then
$w\in S,$
then
![]() $w[\bigcup \limits _{n\in L}Y_{n}]\in $
tr(ctble).
$w[\bigcup \limits _{n\in L}Y_{n}]\in $
tr(ctble).
Given
![]() $W\subseteq L,$
define
$W\subseteq L,$
define
![]() $\overline {W}=\bigcup \limits _{n\in W}Y_{n}.$
Let
$\overline {W}=\bigcup \limits _{n\in W}Y_{n}.$
Let
![]() $w\in S,$
our task is to show that
$w\in S,$
our task is to show that
![]() $w\left [ \overline {L}\right ] $
is in tr(ctble). We proceed by cases:
$w\left [ \overline {L}\right ] $
is in tr(ctble). We proceed by cases:
Case 84.
![]() $L\in D_{0}\left ( w\right ) .$
$L\in D_{0}\left ( w\right ) .$
Let
![]() $r\in 2^{\omega }, n\in \omega $
and
$r\in 2^{\omega }, n\in \omega $
and
![]() $\left \{ r_{i}\mid i\in L\wedge i>n\right \} \subseteq 2^{\omega }$
witnessing that
$\left \{ r_{i}\mid i\in L\wedge i>n\right \} \subseteq 2^{\omega }$
witnessing that
![]() $L\in D_{0}\left ( w\right ) .$
Now, find
$L\in D_{0}\left ( w\right ) .$
Now, find
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $k>n$
and
$k>n$
and
![]() $f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $
for every
$f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $
for every
![]() $m\geq k.$
Define
$m\geq k.$
Define
![]() $W=L\setminus k.$
We know that
$W=L\setminus k.$
We know that
![]() $w\left [ Y_{i}\right ] \in $
tr(ctble) for all
$w\left [ Y_{i}\right ] \in $
tr(ctble) for all
![]() $i\in L,$
so in order to prove that
$i\in L,$
so in order to prove that
![]() $w\left [ \overline {L}\right ] \in $
tr(ctble), it is enough to show that
$w\left [ \overline {L}\right ] \in $
tr(ctble), it is enough to show that
![]() $w\left [ \overline {W}\right ] \in $
tr(ctble).
$w\left [ \overline {W}\right ] \in $
tr(ctble).
We know that
![]() $w\left [ \overline {W}\right ] =\bigcup \left \{ w\left [ Y_{m}\right ] \mid m\in W\right \} .$
Now, if
$w\left [ \overline {W}\right ] =\bigcup \left \{ w\left [ Y_{m}\right ] \mid m\in W\right \} .$
Now, if
![]() $m\in W,$
then
$m\in W,$
then
![]() $f_{w}\left ( m\right ) \subseteq g\left ( m\right ) ,$
which implies that
$f_{w}\left ( m\right ) \subseteq g\left ( m\right ) ,$
which implies that
![]() $Y_{m} =Z_{m}\setminus g\left ( m\right ) \subseteq Z_{m}\setminus f_{w}\left ( m\right ) ,$
so
$Y_{m} =Z_{m}\setminus g\left ( m\right ) \subseteq Z_{m}\setminus f_{w}\left ( m\right ) ,$
so
![]() $w\left [ Y_{m}\right ] $
is a comb with base
$w\left [ Y_{m}\right ] $
is a comb with base
![]() $r_{m}.$
By Lemma 74, it follows that
$r_{m}.$
By Lemma 74, it follows that
![]() $w\left [ \overline {W}\right ] \in $
tr(ctble).
$w\left [ \overline {W}\right ] \in $
tr(ctble).
Case 85.
![]() $L\in D_{1}\left ( w\right ) .$
$L\in D_{1}\left ( w\right ) .$
Let
![]() $r\in 2^{\omega }$
and
$r\in 2^{\omega }$
and
![]() $n\in \omega $
witnessing that
$n\in \omega $
witnessing that
![]() $L\in D_{1}\left ( w\right ) .$
Now, find
$L\in D_{1}\left ( w\right ) .$
Now, find
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $k>n$
and
$k>n$
and
![]() $f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $
for every
$f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $
for every
![]() $m\geq k.$
Define
$m\geq k.$
Define
![]() $W=L\setminus k.$
It is enough to prove that
$W=L\setminus k.$
It is enough to prove that
![]() $w\left [ \overline {W}\right ] \in $
tr(ctble).
$w\left [ \overline {W}\right ] \in $
tr(ctble).
We know that
![]() $w\left [ \overline {W}\right ] =\bigcup \left \{ w\left [ Y_{m}\right ] \mid m\in W\right \} .$
Moreover, if
$w\left [ \overline {W}\right ] =\bigcup \left \{ w\left [ Y_{m}\right ] \mid m\in W\right \} .$
Moreover, if
![]() $m\in W,$
then
$m\in W,$
then
![]() $Y_{m}\subseteq Z_{m}\setminus f_{w}\left ( m\right ) ,$
so
$Y_{m}\subseteq Z_{m}\setminus f_{w}\left ( m\right ) ,$
so
![]() $w\left [ Y_{m}\right ] $
is a comb with base
$w\left [ Y_{m}\right ] $
is a comb with base
![]() $r.$
By Lemma 75, it follows that
$r.$
By Lemma 75, it follows that
![]() $w\left [ \overline {W}\right ] \in $
tr(ctble).
$w\left [ \overline {W}\right ] \in $
tr(ctble).
Case 86.
![]() $L\in D_{2}\left ( w\right ) .$
$L\in D_{2}\left ( w\right ) .$
Let
![]() $d\in 2^{\omega }$
and
$d\in 2^{\omega }$
and
![]() $n\in \omega $
witnessing that
$n\in \omega $
witnessing that
![]() $L\in D_{2}\left ( w\right ) .$
Find
$L\in D_{2}\left ( w\right ) .$
Find
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $k>n$
and
$k>n$
and
![]() $f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $
for every
$f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $
for every
![]() $m\geq k.$
Define
$m\geq k.$
Define
![]() $W=L\setminus k.$
It is enough to prove that
$W=L\setminus k.$
It is enough to prove that
![]() $w\left [ \overline {W}\right ] \in $
tr(ctble). This is trivial since
$w\left [ \overline {W}\right ] \in $
tr(ctble). This is trivial since
![]() $w\left [ \overline {W}\right ] \subseteq \widehat {d}.$
$w\left [ \overline {W}\right ] \subseteq \widehat {d}.$
Case 87.
![]() $L\in D_{3}\left ( w\right ) .$
$L\in D_{3}\left ( w\right ) .$
Let
![]() $d\in 2^{\omega }, n\in \omega $
and
$d\in 2^{\omega }, n\in \omega $
and
![]() $\left \{ d_{i}\mid i\in L\wedge i>n\right \} \subseteq 2^{\omega }$
witnessing that
$\left \{ d_{i}\mid i\in L\wedge i>n\right \} \subseteq 2^{\omega }$
witnessing that
![]() $L\in D_{3}\left ( w\right ) .$
Find
$L\in D_{3}\left ( w\right ) .$
Find
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $k>n$
and
$k>n$
and
![]() $f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $
for every
$f_{w}\left ( m\right ) \subseteq g\left ( m\right ) $
for every
![]() $m\geq k.$
It is enough to prove that
$m\geq k.$
It is enough to prove that
![]() $w\left [ \overline {W}\right ] \in $
tr(ctble). This is easy because
$w\left [ \overline {W}\right ] \in $
tr(ctble). This is easy because
![]() $w[\overline {W}]\subseteq \bigcup \{\widehat {d}_{i}\mid i\in L\wedge i>n\}.$
$w[\overline {W}]\subseteq \bigcup \{\widehat {d}_{i}\mid i\in L\wedge i>n\}.$
This finishes the proof.
By combining Propositions 67 and 79 and Theorem 60, we conclude the following:
Corollary 88.
![]() $\mathfrak {h=c}$
implies that there is a weakly tight, Katětov maximal MAD family that is
$\mathfrak {h=c}$
implies that there is a weakly tight, Katětov maximal MAD family that is
![]() $\mathbb {S}\,$
-destructible.
$\mathbb {S}\,$
-destructible.
We can now answer an open question posed in [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1]. Until now, the only known Katětov maximal MAD families were tight. This lead Arciga, Hrušák, and Martínez to ask the following:
Problem 89 (Arciga, Hrušák, and Martínez).
Does there exist a MAD family maximal in the Katětov order that is weakly tight but not tight?
The MAD family of Corollary 88 is such an example. Since it is Sacks destructible, it is also Cohen destructible, hence it can not be tight.
A trivial consequence of Corollary 88, is that
![]() $\mathfrak {h=c}$
implies that there is a MAD family such that all MAD families Katětov above it are Sacks destructible. We do not know if this is always the case.
$\mathfrak {h=c}$
implies that there is a MAD family such that all MAD families Katětov above it are Sacks destructible. We do not know if this is always the case.
Problem 90. Is the statement “For every MAD family
![]() $\mathcal {A},$
is there is a Sacks indestructible MAD family
$\mathcal {A},$
is there is a Sacks indestructible MAD family
![]() $\mathcal {B}$
such that
$\mathcal {B}$
such that
![]() $\mathcal {A}\leq _{\textsf {K}}\mathcal {B} $
” consistent? What about for Cohen indestructibility?
$\mathcal {A}\leq _{\textsf {K}}\mathcal {B} $
” consistent? What about for Cohen indestructibility?
We now turn our attention to Laflamme MAD families. We start with the following definition:
Definition 91
-
1. Let
 $\varphi :\mathcal {P}\left ( \omega \right ) \longrightarrow \mathbb {R\cup }\left \{ \infty \right \} $
such that if
$\varphi :\mathcal {P}\left ( \omega \right ) \longrightarrow \mathbb {R\cup }\left \{ \infty \right \} $
such that if
 $A\subseteq \omega ,$
then
$A\subseteq \omega ,$
then
 $\varphi \left ( A\right ) =\sum \limits _{n\in A}\frac {1}{n+1}.$
$\varphi \left ( A\right ) =\sum \limits _{n\in A}\frac {1}{n+1}.$
-
2. The summable ideal is
 $\mathcal {J}_{\frac {1}{n} }=\{A\subseteq \omega \mid \varphi \left ( A\right ) <\infty \}.$
$\mathcal {J}_{\frac {1}{n} }=\{A\subseteq \omega \mid \varphi \left ( A\right ) <\infty \}.$
It is easy to see that
![]() $\mathcal {J}_{\frac {1}{n}}$
is a tall
$\mathcal {J}_{\frac {1}{n}}$
is a tall
![]() $F_{\sigma } $
-ideal. This ideal (and its generalizations) have been extensively studied in the past. To learn more, the reader may consult [Reference Cancino-Manríquez12, Reference Farah21, Reference Flašková25, Reference Flašková24, Reference Guzmán-González and Meza-Alcántara33, Reference Hernández-Hernández and Hrušák35, Reference Hrušák39, Reference Hrušák and Minami41]. We now proceed to prove the following:
$F_{\sigma } $
-ideal. This ideal (and its generalizations) have been extensively studied in the past. To learn more, the reader may consult [Reference Cancino-Manríquez12, Reference Farah21, Reference Flašková25, Reference Flašková24, Reference Guzmán-González and Meza-Alcántara33, Reference Hernández-Hernández and Hrušák35, Reference Hrušák39, Reference Hrušák and Minami41]. We now proceed to prove the following:
Proposition 92 (
 $\mathfrak {h=c}$
).
$\mathfrak {h=c}$
).
The summable ideal
![]() $\mathcal {J}_{\frac {1}{n}}$
is injectively nice.
$\mathcal {J}_{\frac {1}{n}}$
is injectively nice.
Proof Let
![]() $S\subseteq $
Inj
$S\subseteq $
Inj
![]() $\left ( \omega \right ) $
of size less that
$\left ( \omega \right ) $
of size less that
![]() $\mathfrak {c}$
and
$\mathfrak {c}$
and
![]() $\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega }.$
Since
$\left \{ X_{n}\mid n\in \omega \right \} \subseteq \left [ \omega \right ] ^{\omega }.$
Since
![]() $\left \vert S\right \vert <\mathfrak {h},$
for all
$\left \vert S\right \vert <\mathfrak {h},$
for all
![]() $n\in \omega $
we can find
$n\in \omega $
we can find
![]() $Z_{n}\in \left [ X_{n}\right ] ^{\omega }$
with the property that
$Z_{n}\in \left [ X_{n}\right ] ^{\omega }$
with the property that
![]() $\varphi (w\left [ Z_{n}\right ] )\in \mathcal {J}_{\frac {1} {n}}.$
For every
$\varphi (w\left [ Z_{n}\right ] )\in \mathcal {J}_{\frac {1} {n}}.$
For every
![]() $w\in S,$
define the function
$w\in S,$
define the function
![]() $f_{w}:\omega \longrightarrow \omega $
such that for any
$f_{w}:\omega \longrightarrow \omega $
such that for any
![]() $n\in \omega ,$
we choose
$n\in \omega ,$
we choose
![]() $f_{w}\left ( n\right ) $
big enough so that
$f_{w}\left ( n\right ) $
big enough so that
![]() $\varphi (w\left [ Z_{n}\right ] \diagup f_{w}\left ( n\right ) )<\frac {1}{2^{n+1}}.$
This is possible since each
$\varphi (w\left [ Z_{n}\right ] \diagup f_{w}\left ( n\right ) )<\frac {1}{2^{n+1}}.$
This is possible since each
![]() $\varphi (w\left [ Z_{n}\right ] )$
is in the summable ideal.
$\varphi (w\left [ Z_{n}\right ] )$
is in the summable ideal.
Since S has size less than
![]() $\mathfrak {b},$
we can find an increasing function
$\mathfrak {b},$
we can find an increasing function
![]() $g\in \omega ^{\omega }$
dominating each
$g\in \omega ^{\omega }$
dominating each
![]() $f_{w}.$
For every
$f_{w}.$
For every
![]() $n\in \omega $
let
$n\in \omega $
let
![]() $Y_{n}=Z_{n}\setminus g\left ( n\right ) $
and
$Y_{n}=Z_{n}\setminus g\left ( n\right ) $
and
![]() $Y=\bigcup \limits _{n\in \omega }Y_{n}.$
It is easy to see that
$Y=\bigcup \limits _{n\in \omega }Y_{n}.$
It is easy to see that
![]() $w\left [ Y\right ] \in \mathcal {J} _{\frac {1}{n}}$
for every
$w\left [ Y\right ] \in \mathcal {J} _{\frac {1}{n}}$
for every
![]() $w\in S.$
$w\in S.$
By combining Propositions 67 and 92, we get the following:
Corollary 93.
![]() $\mathfrak {h=c}$
implies that there is a weakly tight, Katětov maximal MAD family contained in the summable ideal. In particular, there is a Katětov maximal MAD family that is not Laflamme.
$\mathfrak {h=c}$
implies that there is a weakly tight, Katětov maximal MAD family contained in the summable ideal. In particular, there is a Katětov maximal MAD family that is not Laflamme.
The attentive reader will note that the proofs of Propositions 67 and 92 actually show that the MAD family above can constructed to be tight, not just weakly tight. In [Reference Hernández-Hernández and Hrušák35], it was proved that
![]() $\mathcal {J}_{\frac {1}{n}}$
is Random indestructible (see [Reference Bartoszyński and Judah3] for the definition and main properties of Random forcing). In this way,
$\mathcal {J}_{\frac {1}{n}}$
is Random indestructible (see [Reference Bartoszyński and Judah3] for the definition and main properties of Random forcing). In this way,
![]() $\mathfrak {h=c}$
implies that there is a Katětov maximal MAD family that is Cohen indestructible and Random destructible. Ideals and MAD families that are indestructible under some forcings but destructible with another have been studied in [Reference Brendle and Yatabe9, Reference Hrušák and Ferreira40].
$\mathfrak {h=c}$
implies that there is a Katětov maximal MAD family that is Cohen indestructible and Random destructible. Ideals and MAD families that are indestructible under some forcings but destructible with another have been studied in [Reference Brendle and Yatabe9, Reference Hrušák and Ferreira40].
7 The Cohen model
In a private communication, Michael Hrušák suggested to us to investigate if there is a Katětov maximal MAD family of size
![]() $\omega _{1}$
in the Cohen model. At first, the author believed that the parametrized diamond
$\omega _{1}$
in the Cohen model. At first, the author believed that the parametrized diamond
![]() $\Diamond ($
non
$\Diamond ($
non
![]() $\left ( \mathcal {M}\right ) )$
(see [Reference Moore, Hrušák and Džamonja58]) might imply that there is such a family, but we were unable to prove it. We then tried to use CH to construct a Katětov maximal MAD family that would remain Katětov maximal after adding Cohen reals, but this also failed. Finally, we realized that there are no small Katětov maximal MAD families in the Cohen model. In this section we present the proof.
$\left ( \mathcal {M}\right ) )$
(see [Reference Moore, Hrušák and Džamonja58]) might imply that there is such a family, but we were unable to prove it. We then tried to use CH to construct a Katětov maximal MAD family that would remain Katětov maximal after adding Cohen reals, but this also failed. Finally, we realized that there are no small Katětov maximal MAD families in the Cohen model. In this section we present the proof.
In this paper, the incarnation of Cohen forcing we choose to use is
![]() $\mathbb {C}=2^{<\omega }$
ordered by extension. If
$\mathbb {C}=2^{<\omega }$
ordered by extension. If
![]() $G\subseteq \mathbb {C}$
is a generic filter, the associated Cohen real is
$G\subseteq \mathbb {C}$
is a generic filter, the associated Cohen real is
![]() $\left \{ n\in \omega \mid \bigcup G\left ( n\right ) =1\right \} .$
If
$\left \{ n\in \omega \mid \bigcup G\left ( n\right ) =1\right \} .$
If
![]() $\kappa $
is a cardinal, denote by
$\kappa $
is a cardinal, denote by
![]() $\mathbb {C}_{\kappa }$
the finite support product of
$\mathbb {C}_{\kappa }$
the finite support product of
![]() $\kappa $
copies of
$\kappa $
copies of
![]() $\mathbb {C}.$
Given
$\mathbb {C}.$
Given
![]() $X\subseteq \kappa ,$
by
$X\subseteq \kappa ,$
by
![]() $\mathbb {C}_{X}$
denote
$\mathbb {C}_{X}$
denote
![]() $\prod \limits _{\alpha \in X}^{FS}\mathbb {C}$
and we view it as a suborder of
$\prod \limits _{\alpha \in X}^{FS}\mathbb {C}$
and we view it as a suborder of
![]() $\mathbb {C}_{\kappa }.$
It is well known that if a MAD family is
$\mathbb {C}_{\kappa }.$
It is well known that if a MAD family is
![]() $\mathbb {C}$
-indestructible, then it is
$\mathbb {C}$
-indestructible, then it is
![]() $\mathbb {C}_{\kappa }$
-indestructible for every cardinal
$\mathbb {C}_{\kappa }$
-indestructible for every cardinal
![]() $\kappa .$
$\kappa .$
Let
![]() $\mathcal {A}$
be an AD family and
$\mathcal {A}$
be an AD family and
![]() $B\in \mathcal {I(A)}.$
We say that B is
$B\in \mathcal {I(A)}.$
We say that B is
![]() $\mathcal {A}$
-saturated if there are
$\mathcal {A}$
-saturated if there are
![]() $A_{0},\dots ,A_{n} \in \mathcal {A}$
such that
$A_{0},\dots ,A_{n} \in \mathcal {A}$
such that
![]() $B=A_{0}\cup \dots \cup A_{n}.$
Note that if B is
$B=A_{0}\cup \dots \cup A_{n}.$
Note that if B is
![]() $\mathcal {A}$
-saturated, then
$\mathcal {A}$
-saturated, then
![]() $B=\bigcup \{A\in \mathcal {A}\mid \left \vert A\cap B\right \vert =\omega \}.$
Given
$B=\bigcup \{A\in \mathcal {A}\mid \left \vert A\cap B\right \vert =\omega \}.$
Given
![]() $D\in \mathcal {I}(\mathcal {A}),$
we say that B is the
$D\in \mathcal {I}(\mathcal {A}),$
we say that B is the
![]() $\mathcal {A}$
-saturation of D if
$\mathcal {A}$
-saturation of D if
![]() $B=\bigcup \{A\in \mathcal {A}\mid \left \vert A\cap D\right \vert =\omega \}.$
It is easy to see that if B is the
$B=\bigcup \{A\in \mathcal {A}\mid \left \vert A\cap D\right \vert =\omega \}.$
It is easy to see that if B is the
![]() $\mathcal {A}$
-saturation of
$\mathcal {A}$
-saturation of
![]() $D,$
then
$D,$
then
![]() $D\setminus B$
is finite.
$D\setminus B$
is finite.
Proposition 94. Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
two
$\mathcal {B}$
two
![]() $\mathbb {C}$
-indestructible MAD families and
$\mathbb {C}$
-indestructible MAD families and
![]() $\kappa $
a regular cardinal. If
$\kappa $
a regular cardinal. If
![]() $\dot {C}_{gen}$
is the
$\dot {C}_{gen}$
is the
![]() $\mathbb {C}_{\kappa }$
-name of the Cohen generic real added by the first component, then
$\mathbb {C}_{\kappa }$
-name of the Cohen generic real added by the first component, then
![]() $\mathbb {C}_{\kappa }\Vdash $
“
$\mathbb {C}_{\kappa }\Vdash $
“
![]() $\mathcal {A} \upharpoonright \dot {C}_{gen} \nleq _{\textsf {SK}} \mathcal {B} $
.”
$\mathcal {A} \upharpoonright \dot {C}_{gen} \nleq _{\textsf {SK}} \mathcal {B} $
.”
Proof First note that
![]() $\dot {C}_{gen}$
is forced to be in
$\dot {C}_{gen}$
is forced to be in
![]() $\mathcal {I(A)}^{+},$
since the Cohen generic real has infinite intersection with every ground model infinite subset of
$\mathcal {I(A)}^{+},$
since the Cohen generic real has infinite intersection with every ground model infinite subset of
![]() $\omega .$
We also know that both
$\omega .$
We also know that both
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
remain MAD families. We argue by contradiction, assume there is a condition
$\mathcal {B}$
remain MAD families. We argue by contradiction, assume there is a condition
![]() $\overline {p}$
and
$\overline {p}$
and
![]() $\dot {g}$
a
$\dot {g}$
a
![]() $\mathbb {C}_{\kappa }$
-name for a function such that
$\mathbb {C}_{\kappa }$
-name for a function such that
![]() $\overline {p}$
forces that
$\overline {p}$
forces that
![]() $\dot {g}$
is a strong Katětov function from
$\dot {g}$
is a strong Katětov function from
![]() $(\omega ,\mathcal {B)}$
to
$(\omega ,\mathcal {B)}$
to
![]() $(\dot {C}_{gen} ,\mathcal {A}\upharpoonright \dot {C}_{gen}).$
By standard forcing arguments, we can find
$(\dot {C}_{gen} ,\mathcal {A}\upharpoonright \dot {C}_{gen}).$
By standard forcing arguments, we can find
![]() $Z\in \left [ \kappa \right ] ^{\omega }$
such that
$Z\in \left [ \kappa \right ] ^{\omega }$
such that
![]() $\overline {p} \in \mathbb {C}_{Z}$
and both
$\overline {p} \in \mathbb {C}_{Z}$
and both
![]() $\dot {C}_{gen}$
and
$\dot {C}_{gen}$
and
![]() $\dot {g}$
are
$\dot {g}$
are
![]() $\mathbb {C}_{Z}$
-names.
$\mathbb {C}_{Z}$
-names.
Claim 95. There are
![]() $p\in \mathbb {C}_{Z}$
,
$p\in \mathbb {C}_{Z}$
,
![]() $\mathcal {B}_{1}\in \lbrack \mathcal {B} ]^{\omega _{1}}, s,t\in \left [ \omega \right ] ^{<\omega }$
and a family
$\mathcal {B}_{1}\in \lbrack \mathcal {B} ]^{\omega _{1}}, s,t\in \left [ \omega \right ] ^{<\omega }$
and a family
![]() $\{(A_{B},D_{B})\mid B\in \mathcal {B}_{1}\}$
with the following properties
$\{(A_{B},D_{B})\mid B\in \mathcal {B}_{1}\}$
with the following properties
![]() $:$
$:$
-
1.
 $p\leq \overline {p}.$
$p\leq \overline {p}.$
-
2.
 $A_{B}\in \mathcal {I(A)}$
and is
$A_{B}\in \mathcal {I(A)}$
and is
 $\mathcal {A}$
-saturated.
$\mathcal {A}$
-saturated. -
3. If
 $B\in \mathcal {B}_{1},$
then
$B\in \mathcal {B}_{1},$
then
 $p\Vdash $
“
$p\Vdash $
“
 $A_{B}$
is the
$A_{B}$
is the
 $\mathcal {A}$
-saturation of
$\mathcal {A}$
-saturation of
 $\dot {g}[B]$
” and
$\dot {g}[B]$
” and
 $p\Vdash $
“
$p\Vdash $
“
 $\dot {g}\left [ B\right ] \setminus A_{B}=s$
” (so
$\dot {g}\left [ B\right ] \setminus A_{B}=s$
” (so
 $p\Vdash $
“
$p\Vdash $
“
 $\dot {g}\left [ B\right ] \subseteq A_{B}\cup s$
”)
$\dot {g}\left [ B\right ] \subseteq A_{B}\cup s$
”)
 $.$
$.$
-
4.
 $D_{B}\in \mathcal {I(B)}$
and is
$D_{B}\in \mathcal {I(B)}$
and is
 $\mathcal {B}$
-saturated.
$\mathcal {B}$
-saturated. -
5. If
 $B\in \mathcal {B}_{1},$
then
$B\in \mathcal {B}_{1},$
then
 $p\Vdash $
“
$p\Vdash $
“
 $D_{B}$
is the
$D_{B}$
is the
 $\mathcal {B}$
-saturation of
$\mathcal {B}$
-saturation of
 $\dot {g}^{-1}(A_{B}\cup s)$
” and
$\dot {g}^{-1}(A_{B}\cup s)$
” and
 $p\Vdash $
“
$p\Vdash $
“
 $\dot {g}^{-1} (A_{B}\cup s)\setminus D_{B} =t$
” (so
$\dot {g}^{-1} (A_{B}\cup s)\setminus D_{B} =t$
” (so
 $p\Vdash $
“
$p\Vdash $
“
 $\dot {g}^{-1}(A_{B}\cup s)\subseteq D_{B}\cup t$
”)
$\dot {g}^{-1}(A_{B}\cup s)\subseteq D_{B}\cup t$
”)
 $.$
$.$
-
6. The family
 $\{A_{B}\mid B\in \mathcal {B}_{1}\}$
is almost disjoint.
$\{A_{B}\mid B\in \mathcal {B}_{1}\}$
is almost disjoint. -
7. If
 $p_{0}$
is the first coordinate of
$p_{0}$
is the first coordinate of
 $p,$
then
$p,$
then
 $s\subseteq p_{0} ^{-1}\left ( \left \{ 1\right \} \right ) .$
$s\subseteq p_{0} ^{-1}\left ( \left \{ 1\right \} \right ) .$
We prove the claim. For every
![]() $B\in \mathcal {B}$
we find
$B\in \mathcal {B}$
we find
![]() $p_{B}\in \mathbb {C}_{Z}$
,
$p_{B}\in \mathbb {C}_{Z}$
,
![]() $s_{B}, t_{B}\in \left [ \omega \right ] ^{<\omega }$
and
$s_{B}, t_{B}\in \left [ \omega \right ] ^{<\omega }$
and
![]() $A_{B},D_{B}$
that satisfy 1 to 5 above (with
$A_{B},D_{B}$
that satisfy 1 to 5 above (with
![]() $p_{B}$
instead of p,
$p_{B}$
instead of p,
![]() $s_{B}$
instead of s and
$s_{B}$
instead of s and
![]() $t_{B}$
instead of t). Since
$t_{B}$
instead of t). Since
![]() $\mathbb {C}_{Z}$
is countable and
$\mathbb {C}_{Z}$
is countable and
![]() $\mathcal {B}$
is uncountable, we can find
$\mathcal {B}$
is uncountable, we can find
![]() $\mathcal {B}_{2} \in \mathcal {[B]}^{\omega _{1}}$
and
$\mathcal {B}_{2} \in \mathcal {[B]}^{\omega _{1}}$
and
![]() $p\in \mathbb {C}_{Z}, s,t\in \left [ \omega \right ] ^{<\omega }$
such that if
$p\in \mathbb {C}_{Z}, s,t\in \left [ \omega \right ] ^{<\omega }$
such that if
![]() $B\in \mathcal {B}_{2},$
then
$B\in \mathcal {B}_{2},$
then
![]() $p_{B}=p,$
$p_{B}=p,$
![]() $s_{B}=s$
, and
$s_{B}=s$
, and
![]() $t_{B}=t.$
Note that since p forces that s is contained in the image of
$t_{B}=t.$
Note that since p forces that s is contained in the image of
![]() $\dot {g},$
it follows that
$\dot {g},$
it follows that
![]() $s\subseteq p_{0}^{-1}\left ( \left \{ 1\right \} \right ) $
(where
$s\subseteq p_{0}^{-1}\left ( \left \{ 1\right \} \right ) $
(where
![]() $p_{0}$
is the first coordinate of p). We got all the points of the claim, except possibly point 6.
$p_{0}$
is the first coordinate of p). We got all the points of the claim, except possibly point 6.
For every
![]() $B\in \mathcal {B}_{2},$
define
$B\in \mathcal {B}_{2},$
define
![]() $F_{B}=\{E\in \mathcal {A\mid }\left \vert A_{B}\cap E\right \vert =\omega \}.$
We know that
$F_{B}=\{E\in \mathcal {A\mid }\left \vert A_{B}\cap E\right \vert =\omega \}.$
We know that
![]() $A_{B}=\bigcup F_{B},$
each
$A_{B}=\bigcup F_{B},$
each
![]() $F_{B}$
is finite and p forces that every element of
$F_{B}$
is finite and p forces that every element of
![]() $F_{B}$
has infinite intersection with
$F_{B}$
has infinite intersection with
![]() $\dot {g}\left [ B\right ] .$
We now look at the set
$\dot {g}\left [ B\right ] .$
We now look at the set
![]() $\{F_{B}\mid B\in \mathcal {B}_{2}\}.$
We can apply the Delta System Lemma (see [Reference Kunen50]) and find
$\{F_{B}\mid B\in \mathcal {B}_{2}\}.$
We can apply the Delta System Lemma (see [Reference Kunen50]) and find
![]() $\mathcal {B}_{1}\in \lbrack \mathcal {B}_{2}]^{\omega _{1} }$
and
$\mathcal {B}_{1}\in \lbrack \mathcal {B}_{2}]^{\omega _{1} }$
and
![]() $R\subseteq \mathcal {A}$
finite such that
$R\subseteq \mathcal {A}$
finite such that
![]() $\{F_{B}\mid B\in \mathcal {B}_{1}\}$
is a delta system with root
$\{F_{B}\mid B\in \mathcal {B}_{1}\}$
is a delta system with root
![]() $R.$
However, we claim that R is in fact the empty set. Suppose this is not the case, choose
$R.$
However, we claim that R is in fact the empty set. Suppose this is not the case, choose
![]() $E\in R.$
As mentioned before, it follows that
$E\in R.$
As mentioned before, it follows that
![]() $p\Vdash $
“
$p\Vdash $
“
![]() $\dot {g}[B]\cap E$
is infinite” for every
$\dot {g}[B]\cap E$
is infinite” for every
![]() $B\in \mathcal {B}_{1}.$
In this way, p forces that
$B\in \mathcal {B}_{1}.$
In this way, p forces that
![]() $\dot {g}^{-1}\left ( E\right ) $
has infinite intersection with uncountably many elements of
$\dot {g}^{-1}\left ( E\right ) $
has infinite intersection with uncountably many elements of
![]() $\mathcal {B},$
which is a contradiction since
$\mathcal {B},$
which is a contradiction since
![]() $\dot {g}$
is forced to be a Katětov function. We conclude that
$\dot {g}$
is forced to be a Katětov function. We conclude that
![]() $R=\emptyset $
and this finishes the proof of the claim.
$R=\emptyset $
and this finishes the proof of the claim.
We continue with the proof. Define the function
![]() $g^{+}:\omega \longrightarrow \mathcal {P}\left ( \omega \right ) $
where
$g^{+}:\omega \longrightarrow \mathcal {P}\left ( \omega \right ) $
where
![]() In this way,
In this way,
![]() $g^{+}\left ( n\right ) $
is the set of all possible values of
$g^{+}\left ( n\right ) $
is the set of all possible values of
![]() $\dot {g}\left ( n\right ) $
(under the condition p). For every
$\dot {g}\left ( n\right ) $
(under the condition p). For every
![]() $B\in \mathcal {B}_{1}$
and
$B\in \mathcal {B}_{1}$
and
![]() $n\in \omega ,$
we have the following remarks:
$n\in \omega ,$
we have the following remarks:
-
*) If
 $n\in B,$
then
$n\in B,$
then
 $g^{+}\left ( n\right ) \subseteq A_{B}\cup s.$
$g^{+}\left ( n\right ) \subseteq A_{B}\cup s.$
-
**) If
 $n\notin D_{B}\cup t,$
then
$n\notin D_{B}\cup t,$
then
 $g^{+}\left ( n\right ) \cap (A_{B}\cup s)=\emptyset .$
$g^{+}\left ( n\right ) \cap (A_{B}\cup s)=\emptyset .$
In order to prove the first point, note that if
![]() $n\in B,$
then
$n\in B,$
then
![]() $p\Vdash $
“
$p\Vdash $
“
![]() $\dot {g}\left ( n\right ) \in \dot {g}[B]\subseteq A_{B}\cup s,$
” so
$\dot {g}\left ( n\right ) \in \dot {g}[B]\subseteq A_{B}\cup s,$
” so
![]() $g^{+}\left ( n\right ) \subseteq A_{B}\cup s.$
For the second point, if
$g^{+}\left ( n\right ) \subseteq A_{B}\cup s.$
For the second point, if
![]() $n\notin D_{B}\cup t,$
then
$n\notin D_{B}\cup t,$
then
![]() $p\Vdash $
“
$p\Vdash $
“
![]() $n\notin D_{B}\cup t,$
” so
$n\notin D_{B}\cup t,$
” so
![]() $p\Vdash $
“
$p\Vdash $
“
![]() $n\notin \dot {g}^{-1}(A_{B}\cup s).$
” It follows that
$n\notin \dot {g}^{-1}(A_{B}\cup s).$
” It follows that
![]() $p\Vdash $
“
$p\Vdash $
“
![]() $g\left ( n\right ) \notin A_{B}\cup s$
,” which implies that
$g\left ( n\right ) \notin A_{B}\cup s$
,” which implies that
![]() $g^{+}\left ( n\right ) \cap (A_{B}\cup s)=\emptyset .$
$g^{+}\left ( n\right ) \cap (A_{B}\cup s)=\emptyset .$
Define
![]() $Y=\{n\mid g^{+}\left ( n\right ) \in \left [ \omega \right ] ^{<\omega }\}.$
We will now prove the following:
$Y=\{n\mid g^{+}\left ( n\right ) \in \left [ \omega \right ] ^{<\omega }\}.$
We will now prove the following:
Claim 96. The set
![]() $\{B\in \mathcal {B}_{1}\mid B\cap (\omega \setminus Y)\neq \emptyset \}$
is at most countable.
$\{B\in \mathcal {B}_{1}\mid B\cap (\omega \setminus Y)\neq \emptyset \}$
is at most countable.
We will prove something much stronger: we will show that if
![]() $n\notin Y,$
then there is at most one element of
$n\notin Y,$
then there is at most one element of
![]() $\mathcal {B}_{1}$
that has contains
$\mathcal {B}_{1}$
that has contains
![]() $n.$
Assume this is not the case, so there is
$n.$
Assume this is not the case, so there is
![]() $n\notin Y$
and
$n\notin Y$
and
![]() $B_{1},B_{2}\in Y$
for which
$B_{1},B_{2}\in Y$
for which
![]() $n\in B_{1}\cap B_{2}.$
By point *) above, it follows that
$n\in B_{1}\cap B_{2}.$
By point *) above, it follows that
![]() $g^{+}\left ( n\right ) \subseteq \left ( A_{B_{1}}\cup s\right ) \cap \left ( A_{B_{2}}\cup s\right ) .$
But this is a contradiction, since
$g^{+}\left ( n\right ) \subseteq \left ( A_{B_{1}}\cup s\right ) \cap \left ( A_{B_{2}}\cup s\right ) .$
But this is a contradiction, since
![]() $A_{B_{1}}$
and
$A_{B_{1}}$
and
![]() $A_{B_{2}}$
are almost disjoint, yet
$A_{B_{2}}$
are almost disjoint, yet
![]() $g^{+}\left ( n\right ) $
is infinite. This finishes the proof of the claim.
$g^{+}\left ( n\right ) $
is infinite. This finishes the proof of the claim.
Define
![]() $u=\{i\in p_{0}^{-1}\left ( \left \{ 1\right \} \right ) \mid \exists B\in \mathcal {B}_{1}\left ( i\in A_{B}\cup s\right ) \}.$
For each
$u=\{i\in p_{0}^{-1}\left ( \left \{ 1\right \} \right ) \mid \exists B\in \mathcal {B}_{1}\left ( i\in A_{B}\cup s\right ) \}.$
For each
![]() $i\in u,$
choose
$i\in u,$
choose
![]() $B_{i}\in \mathcal {B}_{1}$
such that
$B_{i}\in \mathcal {B}_{1}$
such that
![]() $i\in A_{B_{i}}\cup s.$
Define
$i\in A_{B_{i}}\cup s.$
Define
![]() $A=\bigcup \limits _{i\in u}\left ( A_{B_{i}}\cup s\right ) $
and
$A=\bigcup \limits _{i\in u}\left ( A_{B_{i}}\cup s\right ) $
and
![]() $B=\bigcup \limits _{i\in u}\left ( D_{B_{i}}\cup t\right ) .$
$B=\bigcup \limits _{i\in u}\left ( D_{B_{i}}\cup t\right ) .$
Claim 97.
![]() $p\Vdash $
“
$p\Vdash $
“
![]() $\dot {g}^{-1}\left ( u\right ) \subseteq B$
.”
$\dot {g}^{-1}\left ( u\right ) \subseteq B$
.”
We have the following:

Since
![]() $u\subseteq A,$
it follows that
$u\subseteq A,$
it follows that
![]() $p\Vdash $
“
$p\Vdash $
“
![]() $\dot {g} ^{-1}\left ( u\right ) \subseteq B$
.”
$\dot {g} ^{-1}\left ( u\right ) \subseteq B$
.”
We know that
![]() $\mathcal {B}_{1}$
is uncountable, so appealing to the Claim 96 we can find
$\mathcal {B}_{1}$
is uncountable, so appealing to the Claim 96 we can find
![]() $R\in \mathcal {B}_{1}$
with the following properties:
$R\in \mathcal {B}_{1}$
with the following properties:
-
1.
 $R\subseteq Y.$
$R\subseteq Y.$
-
2. R and B are almost disjoint.
Choose any
![]() $n\in R\setminus B$
and pick any
$n\in R\setminus B$
and pick any
![]() $l>max\left ( g^{+}\left ( n\right ) \right ) ,$
dom
$l>max\left ( g^{+}\left ( n\right ) \right ) ,$
dom
![]() $\left ( p_{0}\right ) $
(recall that
$\left ( p_{0}\right ) $
(recall that
![]() $n\in Y,$
so
$n\in Y,$
so
![]() $g^{+}\left ( n\right ) $
is finite). Now, define
$g^{+}\left ( n\right ) $
is finite). Now, define
![]() $q\in \mathbb {C}_{Z}$
such that
$q\in \mathbb {C}_{Z}$
such that
![]() $q\leq p$
and if
$q\leq p$
and if
![]() $q_{0}$
is the first component of
$q_{0}$
is the first component of
![]() $q,$
then dom
$q,$
then dom
![]() $\left ( q\left ( 0\right ) \right ) =l$
and if
$\left ( q\left ( 0\right ) \right ) =l$
and if
![]() $i\in l\setminus $
dom
$i\in l\setminus $
dom
![]() $\left ( p_{0}\right ) ,$
then
$\left ( p_{0}\right ) ,$
then
![]() $q_{0}\left ( i\right ) =0.$
It follows that
$q_{0}\left ( i\right ) =0.$
It follows that
![]() $q\Vdash $
“
$q\Vdash $
“
![]() $\dot {C}_{gen}\cap l=p_{0}^{-1}\left ( \left \{ 1\right \} \right ) $
.” Note that
$\dot {C}_{gen}\cap l=p_{0}^{-1}\left ( \left \{ 1\right \} \right ) $
.” Note that
![]() $q\Vdash $
“
$q\Vdash $
“
![]() $\dot {g}\left ( n\right ) \in \dot {C}_{gen}\cap l$
” (
$\dot {g}\left ( n\right ) \in \dot {C}_{gen}\cap l$
” (
![]() $\dot {g}\left ( n\right ) $
is forced to be in l since
$\dot {g}\left ( n\right ) $
is forced to be in l since
![]() $g^{+}\left ( n\right ) \subseteq l$
). In this way, it follows that
$g^{+}\left ( n\right ) \subseteq l$
). In this way, it follows that
![]() $q\Vdash $
“
$q\Vdash $
“
![]() $\dot {g}\left ( n\right ) \in p_{0}^{-1} (\{1\})$
.”
$\dot {g}\left ( n\right ) \in p_{0}^{-1} (\{1\})$
.”
Now we find
![]() $r\leq q$
and
$r\leq q$
and
![]() $j\in p_{0}^{-1}(\{1\})$
such that
$j\in p_{0}^{-1}(\{1\})$
such that
![]() $r\Vdash $
“
$r\Vdash $
“
![]() $\dot {g}\left ( n\right ) =j$
.” Since j is forced to be in
$\dot {g}\left ( n\right ) =j$
.” Since j is forced to be in
![]() $\dot {g}[R],$
it follows that
$\dot {g}[R],$
it follows that
![]() $j\in A_{R}\cup s.$
Since j is also in
$j\in A_{R}\cup s.$
Since j is also in
![]() $p_{0}^{-1}(\{1\}),$
we get that
$p_{0}^{-1}(\{1\}),$
we get that
![]() $j\in u.$
However, by the Claim 97, we get that
$j\in u.$
However, by the Claim 97, we get that
![]() $p\Vdash $
“
$p\Vdash $
“
![]() $n\in \dot {g}^{-1}\left ( u\right ) \subseteq B$
,” which implies that
$n\in \dot {g}^{-1}\left ( u\right ) \subseteq B$
,” which implies that
![]() $n\in B.$
This is a contradiction since
$n\in B.$
This is a contradiction since
![]() $n\in R\setminus B.$
This finishes the proof.
$n\in R\setminus B.$
This finishes the proof.
We can now prove the following:
Theorem 98. Let V be a model of CH and
![]() $\kappa>\omega _{1}$
a regular cardinal.
$\kappa>\omega _{1}$
a regular cardinal.
![]() $\mathbb {C}_{\kappa }$
forces that there are no Katětov uniform MAD families of size
$\mathbb {C}_{\kappa }$
forces that there are no Katětov uniform MAD families of size
![]() $\omega _{1}.$
$\omega _{1}.$
Proof Let
![]() $G\subseteq \mathbb {C}_{\kappa }$
be a generic filter. Assume there is
$G\subseteq \mathbb {C}_{\kappa }$
be a generic filter. Assume there is
![]() $\mathcal {A}\in V\left [ G\right ] $
a Katětov uniform MAD family of size
$\mathcal {A}\in V\left [ G\right ] $
a Katětov uniform MAD family of size
![]() $\omega _{1}.$
Note that
$\omega _{1}.$
Note that
![]() $\mathcal {A}$
most appear in an intermediate extension, so
$\mathcal {A}$
most appear in an intermediate extension, so
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\mathbb {C}$
-indestructible. By Proposition 19, we know that
$\mathbb {C}$
-indestructible. By Proposition 19, we know that
![]() $\mathcal {A}$
has a tight restriction, but since
$\mathcal {A}$
has a tight restriction, but since
![]() $\mathcal {A}$
is uniform, it follows by Lemma 15 that
$\mathcal {A}$
is uniform, it follows by Lemma 15 that
![]() $\mathcal {A}$
is already tight.
$\mathcal {A}$
is already tight.
Let
![]() $X\in \left [ \kappa \right ] ^{\omega _{1}}$
such that
$X\in \left [ \kappa \right ] ^{\omega _{1}}$
such that
![]() $\mathcal {A}\in V\left [ G_{X}\right ] $
(where
$\mathcal {A}\in V\left [ G_{X}\right ] $
(where
![]() $G$
is the restriction of G to
$G$
is the restriction of G to
![]() $\mathbb {C}_{X}$
). We know that
$\mathbb {C}_{X}$
). We know that
![]() $V\left [ G\right ] =V\left [ G_{X}\right ] \left [ G_{\kappa \setminus X}\right ] .$
Let
$V\left [ G\right ] =V\left [ G_{X}\right ] \left [ G_{\kappa \setminus X}\right ] .$
Let
![]() $C_{gen}$
be the first Cohen real added by
$C_{gen}$
be the first Cohen real added by
![]() $\mathbb {C}_{\kappa \setminus X}.$
By the Proposition 94, we get that (in
$\mathbb {C}_{\kappa \setminus X}.$
By the Proposition 94, we get that (in
![]() $V\left [ G\right ] $
)
$V\left [ G\right ] $
)
![]() $\mathcal {A}\upharpoonright C_{gen} \nleq _{\textsf {SK}}$
$\mathcal {A}\upharpoonright C_{gen} \nleq _{\textsf {SK}}$
![]() $\mathcal {A}.$
It follows by Point 5 of Lemma 21 that
$\mathcal {A}.$
It follows by Point 5 of Lemma 21 that
![]() $\mathcal {A}\upharpoonright C_{gen} \nleq _{\textsf {K}}\mathcal {A}.$
$\mathcal {A}\upharpoonright C_{gen} \nleq _{\textsf {K}}\mathcal {A}.$
It is known that in the Cohen model, a MAD family is
![]() $\mathbb {C} $
-indestructible if and only if it has size
$\mathbb {C} $
-indestructible if and only if it has size
![]() $\omega _{1}.$
With the theorem above, it follows that if there are Katětov maximal MAD families in the Cohen model, then all of them are
$\omega _{1}.$
With the theorem above, it follows that if there are Katětov maximal MAD families in the Cohen model, then all of them are
![]() $\mathbb {C}$
-destructible. However, we do not know if there is such family. We conjecture that there are no Katětov maximal MAD families in such model, and we hope Theorem 98 is the first step of the proof.
$\mathbb {C}$
-destructible. However, we do not know if there is such family. We conjecture that there are no Katětov maximal MAD families in such model, and we hope Theorem 98 is the first step of the proof.
Conjecture 99. There are no Katětov maximal MAD families in the Cohen model.
Nevertheless, by Theorem 13, there are weakly tight MAD families of size continuum in the Cohen model. So we could not rule out the possibility that a Katětov uniform, weakly tight MAD family exists in there.
8 Open questions
In this last section, we restate some of the main open problems regarding the Katětov order on MAD families, and add some new ones. The most important problems are the following:
Problem 100 [Reference Hrušák and Ferreira40].
Is it consistent that there is a Katětov-top MAD family?
Problem 101 [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1].
Is it consistent that there are no Katětov maximal MAD families?
The only way we know how to construct Katětov maximal MAD families is by constructing a Katětov uniform, weakly tight MAD family. So the following problem is natural:
Problem 102 [Reference Arciga-Alejandre, Hrušák and Martinez-Ranero1].
Is it consistent that there is a Katětov maximal MAD family that is not weakly tight?
We show that Katětov maximality does not imply tightness, but a completely different idea for weak tightness would be needed.
The results in Section 4 suggest the following:
Problem 103. Does the existence of a completely separable, weakly tight MAD family imply that there is no Katětov-top MAD family?
Regarding the generic existence of uniform MAD families, we ask:
Problem 104. Does the generic existence of uniform MAD families imply non
![]() $\left ( \mathcal {M}\right ) =\mathfrak {a=c}$
?
$\left ( \mathcal {M}\right ) =\mathfrak {a=c}$
?
The results in Section 6 suggest the following:
Problem 105. Is the statement “For every MAD family
![]() $\mathcal {A},$
there is a Sacks indestructible MAD family
$\mathcal {A},$
there is a Sacks indestructible MAD family
![]() $\mathcal {B}$
such that
$\mathcal {B}$
such that
![]() $\mathcal {A}\leq _{\textsf {K}}\mathcal {B} $
” consistent? What about for Cohen indestructibility?
$\mathcal {A}\leq _{\textsf {K}}\mathcal {B} $
” consistent? What about for Cohen indestructibility?
We know there are no small Katětov maximal MAD family in the Cohen model, but we do not know if there are any of them.
Problem 106. Is there a Katětov maximal MAD family in the Cohen model? What about Katětov uniform MAD families?
We also do not know anything about the following:
Problem 107. What can be said about the statement: “For every MAD family
![]() $\mathcal {A},$
there is a Katětov maximal MAD family
$\mathcal {A},$
there is a Katětov maximal MAD family
![]() $\mathcal {B}$
such that
$\mathcal {B}$
such that
![]() $\mathcal {A}\leq _{\textsf {K}}\mathcal {B} $
”?
$\mathcal {A}\leq _{\textsf {K}}\mathcal {B} $
”?
All known constructions of Katětov maximal MAD family yield a MAD family of size
![]() $\mathfrak {c.}$
This led Hrušák to ask the following:
$\mathfrak {c.}$
This led Hrušák to ask the following:
Problem 108 [Reference Hrušák37].
Is it consistent that there is a Katětov maximal MAD family of size less than
![]() $\mathfrak {c}$
?
$\mathfrak {c}$
?
In the past, the author claimed to answer positively the previous problem. Unfortunately, the proof had a mistake. We want to take the opportunity to clarify that the problem remains open.
Acknowledgement
This paper would not have been possible without the valuable teachings from Michael Hrušák. I would like to thank him for being my guide and mentor in this MAD journey.
Funding
The research of the author was supported by a PAPIIT grant IA102222.