Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T14:51:43.579Z Has data issue: false hasContentIssue false
  • English
  • Français

A jump class of noncappable degrees

Published online by Cambridge University Press:  12 March 2014

S. B. Cooper
S. B. Cooper*
Affiliation:
Department of Pure Mathematics, University of Leeds, Leeds LS2 9JT, England
Get access Rights & Permissions [Opens in a new window]

Extract

Friedberg [3] showed that every degree of unsolvability above 0′ is the jump of some degree, and Sacks [9] showed that the degrees above 0′ which are recursively enumerable (r.e.) in 0′ are the jumps of the r.e. degrees.

In this paper we examine the extent to which the Sacks jump theorem can be combined with the minimal pair theorem of Lachlan [4] and Yates [13]. We prove below that there is a degree c > 0′ which is r.e. in 0′ but which is not the jump of half a minimal pair of r.e. degrees.

This extends Yates' result [13] proving the existence of noncappable degrees (that is, r.e. degrees a < 0′ for which there is no corresponding r.e. b > 0 with a ∩ b = 0).

It also throws more light on the class PS of promptly simple degrees. It was shown by Ambos-Spies, Jockusch, Shore and Soare [1] that PS coincides with the class NC of noncappable degrees, and with the class LC of all low-cuppable degrees, and (using earlier work of Maass, Shore and Stob [5]) that PS splits every class Hn or Ln, n ≥ 0, in the high-low hierarchy of r.e. degrees.

If c > 0′, with c r.e. in 0′, let

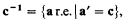
and call c−1 the jump class for c. It is easy to see that every jump class contains members of PS (= NC = LC). By Sacks [8] there exists a low a ∈ LC, where of course [a, 0′] (= {br.e. ∣a ≤ b ≤ 0′}) ⊆ LC = PS. But by Robinson [7] [a, 0′] intersects with every jump class.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 2 , June 1989 , pp. 324 - 353
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ambos-Spies, K.et al., An algebraic decomposition of the recursively enumerable degrees and the coincidence of several degree classes with the promptly simple degrees, Transactions of the American Mathematical Society, vol. 281 (1984), pp. 109–128.CrossRefGoogle Scholar
[2]Bickford, M., The jump operator in strong reducibilities, Ph.D. thesis, University of Wisconsin, Madison, Wisconsin, 1983.Google Scholar
[3]Friedberg, R. M., A criterion for completeness of degrees of unsolvability, this Journal, vol. 22 (1957), pp. 159–160.Google Scholar
[4]Lachlan, A. H., Lower bounds for pairs of recursively enumerable degrees, Proceedings of the London Mathematical Society, ser. 2, vol. 16 (1966), pp. 537–569.CrossRefGoogle Scholar
[5]Maass, W., Shore, R. A. and Stob, M., Splitting properties and jump classes, Israel Journal of Mathematics, vol. 39 (1981), pp. 210–224.CrossRefGoogle Scholar
[6]Miller, D., High recursively enumerable degrees and the anti-cupping property, Logic year 1979–80 (Lerman, M.et al., editors), Lecture Notes in Mathematics, vol. 859, Springer-Verlag, Berlin, 1981, pp. 230–267.CrossRefGoogle Scholar
[7]Robinson, R. W., Jump restricted interpolation in the r.e. degrees, Annals of Mathematics, ser. 2, vol. 93 (1971), pp. 586–596.Google Scholar
[8]Sacks, G. E., Degrees of unsolvability, rev. ed., Princeton University Press, Princeton, New Jersey, 1966.Google Scholar
[9]Sacks, G. E., Recursive enumerability and the jump operator, Transactions of the American Mathematical Society, vol. 108 (1963), pp. 223–239.CrossRefGoogle Scholar
[10]Shore, R. A., A non-inversion theorem for the jump operator, Annals of Pure and Applied Logic (to appear).Google Scholar
[11]Soare, R. I. and Stob, M., Relative recursive enumerability, Proceedings of the Herbrand symposium (Stern, J., editor), North-Holland, Amsterdam, 1982, pp. 299–324.CrossRefGoogle Scholar
[12]Soare, R. I., Tree arguments in recursion theory and the 0‴ priority method, Recursion theory, Proceedings of Symposia in Pure Mathematics, vol. 42, American Mathematical Society, Providence, Rhode Island, 1985, pp. 53–106.CrossRefGoogle Scholar
[13]Yates, C. E. M., A minimal pair of recursively enumerable degrees, this Journal, vol. 31 (1966), pp. 159–168.Google Scholar