Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T10:20:19.405Z Has data issue: false hasContentIssue false
  • English
  • Français

JOINT DIAMONDS AND LAVER DIAMONDS

Published online by Cambridge University Press:  13 June 2019

MIHA E. HABIČ
MIHA E. HABIČ*
Affiliation:
FACULTY OF INFORMATION TECHNOLOGY CZECH TECHNICAL UNIVERSITY IN PRAGUE THÁKUROVA 9 160 00 PRAHA 6, CZECH REPUBLIC and DEPARTMENT OF LOGIC FACULTY OF ARTS CHARLES UNIVERSITY NÁM. JANA PALACHA 2 116 38 PRAHA 1, CZECH REPUBLIC E-mail:[email protected]: https://mhabic.github.io
Get access Rights & Permissions [Opens in a new window]

Abstract

The concept of jointness for guessing principles, specifically 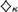${\diamondsuit _\kappa }$ and various Laver diamonds, is introduced. A family of guessing sequences is joint if the elements of any given sequence of targets may be simultaneously guessed by the members of the family. While equivalent in the case of 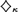${\diamondsuit _\kappa }$, joint Laver diamonds are nontrivial new objects. We give equiconsistency results for most of the large cardinals under consideration and prove sharp separations between joint Laver diamonds of different lengths in the case of θ-supercompact cardinals.

Keywords

03E5503E35Laver functionsjoint Laver functionsjoint diamond sequences
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 3 , September 2019 , pp. 895 - 928
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Apter, A. W., Cummings, J., and Hamkins, J. D., Large cardinals with few measures. Proceedings of the American Mathematical Society, vol. 135 (2007), no. 7, pp. 2291–2300.Google Scholar
Apter, A. W. and Shelah, S., Menas’ result is best possible. Transactions of the American Mathematical Society, vol. 349 (1997), no. 5, pp. 2007–2034.Google Scholar
Ben-Neria, O. and Gitik, M., A model with a unique normal measure on κ and ${2^\kappa } = {\kappa ^{ + + }}$ from optimal assumptions, preprint.Google Scholar
Carmody, E., Force to change large cardinal strength, Ph.D. thesis, The Graduate Center, City University of New York, 2015, ProQuest/UMI Publication No. 3704311.Google Scholar
Corazza, P., Laver sequences for extendible and super-almost-huge cardinals, this Journal, vol. 64 (1999), no. 3, pp. 963–983.Google Scholar
Cummings, J., Iterated forcing and elementary embeddings, Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 775–883.Google Scholar
Dow, A., Good and OK ultrafilters. Transactions of the American Mathematical Society, vol. 290 (1985), no. 1, pp. 145–160.Google Scholar
Friedman, S.-D. and Magidor, M., The number of normal measures, this Journal, vol. 74 (2009), no. 3, pp. 1069–1080.Google Scholar
Gitik, M. and Shelah, S., On certain indestructibility of strong cardinals and a question of Hajnal. Archive for Mathematical Logic, vol. 28 (1989), no. 1, pp. 35–42.Google Scholar
Hamkins, J. D., The lottery preparation. Annals of Pure and Applied Logic, vol. 101 (2000), no. 2–3, pp. 103–146.Google Scholar
Hamkins, J. D., Extensions with the approximation and cover properties have no new large cardinals. Fundamenta Mathematicae, vol. 180 (2003), no. 3, pp. 257–277.Google Scholar
Hamkins, J. D., A class of strong diamond principles, preprint, 2002, arXiv:math/0211419 [math.LO].Google Scholar
Jech, T., Stationary sets, Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 93–128.Google Scholar
Kanamori, A., Perfect-set forcing for uncountable cardinals, Annals of Mathematical Logic, vol. 19 (1980), no. 1–2, pp. 97–114.Google Scholar
Kanamori, A., The Higher Infinite, second ed., Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2008.Google Scholar
Laver, R., Making the supercompactness of κ indestructible under κ-directed closed forcing. Israel Journal of Mathematics, vol. 29 (1978), no. 4, pp. 385–388.Google Scholar
Magidor, M., How large is the first strongly compact cardinal ? or A study on identity crises. Annals of Mathematical Logic, vol. 10 (1976), no. 1, pp. 33–57.Google Scholar
Magidor, M., On the existence of nonregular ultrafilters and the cardinality of ultrapowers. Transactions of the American Mathematical Society, vol. 249 (1979), no. 1, pp. 97–111.Google Scholar
Menas, T. K., On strong compactness and supercompactness. Annals of Mathematical Logic, vol. 7 (1974/75), pp. 327–359.Google Scholar
Shelah, S., Diamonds. Proceedings of the American Mathematical Society, vol. 138 (2010), no. 6, pp. 2151–2161.Google Scholar
Weiß, C., Subtle and ineffable tree properties, Ph.D. thesis, Ludwig-Maximilians-Universität München, 2010.Google Scholar
Zeman, M., Inner Models and Large Cardinals, De Gruyter Series in Logic and its Applications, vol. 5, Walter de Gruyter, Berlin, 2002.Google Scholar