Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T12:59:40.652Z Has data issue: false hasContentIssue false
  • English
  • Français

Jensen's ⃞ principles and the Novák number of partially ordered sets

Published online by Cambridge University Press:  12 March 2014

Boban Veličković
Boban Veličković*
Affiliation:
Mathematical Institute, Belgrade, Yugoslavia
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we consider various properties of Jensen's □ principles and use them to construct several examples concerning the so-called Novák number of partially ordered sets.

In §1 we give the relevant definitions and review some facts about □ principles. Apart from some simple observations most of the results in this section are known.

In §2 we consider the Novák number of partially ordered sets and, using □ principles, give counterexamples to the productivity of this cardinal function. We also formulate a principle, show by forcing that it is consistent and use it to construct an ℵ2-Suslin tree T such that forcing with T × T collapses ℵ1.

In §3 we briefly consider games played on partially ordered sets and relate them to the problems of the previous section. Using a version of □ we give an example of a proper partial order 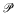such that the game of length ω played on 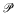is undetermined.

In §4 we raise the question of whether the Novák number of a homogenous partial order can be singular, and show that in some cases the answer is no.

We assume familiarity with the basic techniques of forcing. In §1 some facts about large cardinals (e.g. weakly compact cardinals are 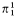-indescribable) and elementary properties of the constructible hierarchy are used. For this and all undefined terms we refer the reader to Jech [10].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 1 , March 1986 , pp. 47 - 58
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCE

[1]Abraham, U. and Shelah, S., Forcing closed unbounded sets, this Journal, vol. 48 (1983), pp. 643–657.Google Scholar
[2]Balcar, B., Pelant, J. and Simon, P., The space of ultrafilters on N covered by nowhere dense sets, Fundamenta Mathematicae, vol. 110 (1980), pp. 11–24.Google Scholar
[3]Baumgartner, J., A new class of order types, Annals of Mathematical Logic, vol. 9 (1976), pp. 187–222.Google Scholar
[4]Baumgartner, J., Applications of the proper forcing axiom, Handbook of set-theoretic topology (Kunen, K. and Vaughan, J., editors), North-Holland, Amsterdam, 1984, pp. 913–959.Google Scholar
[5]Beller, A. and Litman, A., A strengthening of Jensen's □ principles, this Journal, vol. 45 (1980), pp. 251–264.Google Scholar
[6]Burgess, J., Forcing, Handbook of mathematical logic (Barwise, J., editor), North-Holland, Amsterdam, 1977, pp. 403–452.CrossRefGoogle Scholar
[7]Fleissner, W. and Kunen, K., Barely Baire spaces, Fundamenta Mathematicae, vol. 101 (1978), pp. 229–240.CrossRefGoogle Scholar
[8]Foreman, M., Games played on Boolean algebras, this Journal, vol. 48 (1983), pp. 714–723.Google Scholar
[9]Jech, T., A game theoretic property of Boolean algebras, Logic Colloquium '77 (Macintyre, A., Pacholski, L. and Paris, J., editors), North-Holland, Amsterdam, 1978, pp. 135–144.Google Scholar
[10]Jech, T., Set theory, Academic Press, New York, 1978.Google Scholar
[11]Jensen, R., The fine structure of the constructible hierarchy, Annals of Mathematical Logic, vol. 4 (1972), pp. 229–308.Google Scholar
[12]Kanamori, A. and Magidor, M., The evolution of large cardinal axioms in set theory, Higher set theory (Müller, G. and Scott, D., editors), Lecture Notes in Mathematics, vol. 669, Springer-Verlag, Berlin, 1978, pp. 99–275.Google Scholar
[13]Kunen, K., Saturated ideals, this Journal, vol. 43 (1978), pp. 65–76.Google Scholar
[14]Magidor, M., Reflecting stationary sets, this Journal, vol. 47 (1982), pp. 755–771.Google Scholar
[15]Todorčević, S., A note on the proper forcing axiom, Axiomatic set theory (Baumgartner, J.et al., editors), Contemporary Mathematics, vol. 31, American Mathematical Society, Providence, Rhode Island, 1984, pp. 209–218.Google Scholar
[16]Velleman, D., Morasses, diamonds, and forcing, Ph.D. Thesis, University of Wisconsin, Madison, Wisconsin, 1980.Google Scholar
[17]Velleman, D., On a generalization of Jensen's □κ and strategic closure of partial orders, this Journal, vol. 48 (1983), pp. 1046–1053.Google Scholar