Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T13:12:03.317Z Has data issue: false hasContentIssue false
  • English
  • Français

The Jensen Covering Property

Published online by Cambridge University Press:  12 March 2014

E. Schimmerling  and
W. H. Woodin
E. Schimmerling
Affiliation:
Carnegie Mellon University, Department of Mathematical Sciences Pittsburgh, PA 15213-3890., USA, E-Mail: [email protected]
W. H. Woodin
Affiliation:
University of California at Berkeley, Department of Mathematics Berkeley, CA 94720., USA, E-Mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The Jensen covering lemma says that either L has a club class of indiscernibles, or else, for every uncountable set A of ordinals, there is a set B ∈ L with A ⊆ B and card (B) = card(A). One might hope to extend Jensen's covering lemma to richer core models, which for us will mean to inner models of the form L[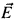] where 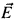is a coherent sequence of extenders of the kind studied in Mitchell-Steel [8], The papers [8], [12], [10] and [1] show how to construct core models with Woodin cardinals and more. But, as Prikry forcing shows, one cannot expect too direct a generalization of Jensen's covering lemma to core models with measurable cardinals.

Recall from [8] that if L[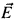] is a core model and α is an ordinal, then either Eα = ∅, or else Eα is an extender over 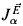As in [8], we assume here that if Eα is an extender, then Eα is below superstrong type in the sense that the set of generators of Eα is bounded in 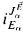(crit(Eα)). Let us say that L[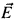] is a lower-part core model iff for every ordinal α, Eα is not a total extender over L[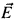]. In other words, if L[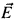] is a lower-part core model, then no cardinal in L[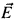] is measurable as witnessed by an extender on 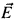. Other than the “below superstrong” hypothesis, we impose no bounds on the large cardinal axioms true in the levels of a lower-part core model.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 4 , December 2001 , pp. 1505 - 1523
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Andretta, A., Neeman, I.. and Steel, J., The domestic levels of Kc are iterable, Israel Journal of Mathematics, to appear.Google Scholar
[2]Dodd, A. J. and Jensen, R. B., The covering lemma for K. Annals of Mathematical Logic, vol. 22 (1982). no. 1. pp. 1–30.CrossRefGoogle Scholar
[3]Dodd, A. J. and Jensen, R. B.. The covering lemma for L[U], Annals of Mathematical Logic, vol. 22 (1982). no. 2. pp. 127–135.CrossRefGoogle Scholar
[4]Kechris, A. and Woodin, W. H.. Equivalence of partition properties and determinacy. Proceedings of the National Academy of Sciences, vol. 80. 1983, pp. 1783–1786.CrossRefGoogle ScholarPubMed
[5]Martin, D. A. and Steel, J. R., Iteration trees. Journal of the American Mathematical Society. vol. 7 (1994), pp. 1–73.CrossRefGoogle Scholar
[6]Mitchell, W. J. and Schimmerling, E., Weak covering without countable closure. Mathematical Researh Letters, vol. 2 (1995). no. 5. pp. 595–609.CrossRefGoogle Scholar
[7]Mitchell, W. J., Schimmerling, E., and Steel, J. R., The covering lemma up to a Woodin cardinal. Annals of Pure and Applied Logic, vol. 84 (1997), no. 2, pp. 219–255.CrossRefGoogle Scholar
[8]Mitchell, W. J. and Steel, J. R.. Fine structure and iteration trees. Lecture Notes in Logic, vol. 3. Springer-Verlag. Berlin, 1994.Google Scholar
[9]Schimmerling, E., Combinatorial principles in the core model for one Woodin cardinal. Annals of Pure and Applied Logic, vol. 74. no. 2, pp. 153–201.CrossRefGoogle Scholar
[10]Schimmerling, E. and Steel, J. R.. Fine structure for tame inner models, this Journal, vol. 61 (1996). no. 2. pp. 621–639.Google Scholar
[11]Steel, J. R., Scales in L(®). Lecture Notes in Mathematics, vol. 1019, pp. 107-156. Lecture Notes in Mathematics. Springer-Verlag. Berlin. 1983, pp. 107-156, also in Cabal Seminar 79-81.Google Scholar
[12]Steel, J. R., Inner models with many Woodin cardinals. Annals of Pure and Applied Logic, vol. 65 (1993). no. 2. pp. 185–209.CrossRefGoogle Scholar
[13]Steel, J. R.The core model iterability problem. Lecture Notes in Logic, vol. 8, Springer-Verlag, Berlin, 1996.CrossRefGoogle Scholar