Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T03:16:34.683Z Has data issue: false hasContentIssue false
  • English
  • Français

ITERATING SYMMETRIC EXTENSIONS

Published online by Cambridge University Press:  14 March 2019

ASAF KARAGILA
ASAF KARAGILA*
Affiliation:
EINSTEIN INSTITUTE OF MATHEMATICS THE HEBREW UNIVERSITY OF JERUSALEM EDMOND J. SAFRA CAMPUS, GIVAT RAM JERUSALEM91904, ISRAEL and SCHOOL OF MATHEMATICS UNIVERSITY OF EAST ANGLIA NORWICH NR4 7TJ, UK E-mail: [email protected]: http://karagila.org
Get access Rights & Permissions [Opens in a new window]

Abstract

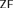The notion of a symmetric extension extends the usual notion of forcing by identifying a particular class of names which forms an intermediate model of $ZF$ between the ground model and the generic extension, and often the axiom of choice fails in these models. Symmetric extensions are generally used to prove choiceless consistency results. We develop a framework for iterating symmetric extensions in order to construct new models of 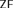$ZF$. We show how to obtain some well-known and lesser-known results using this framework. Specifically, we discuss Kinna–Wagner principles and obtain some results related to their failure.

Keywords

Primary 03E40Secondary 03E25symmetric extensionsiterated forcingiterated symmetriessymmetric iterationaxiom of choiceground model definabilityKinna–Wagner principles
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 1 , March 2019 , pp. 123 - 159
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Blass, A., Injectivity, projectivity, and the axiom of choice. Transactions of the American Mathematical Society, vol. 255 (1979), pp. 31–59.10.1090/S0002-9947-1979-0542870-6CrossRefGoogle Scholar
Feferman, S., Some applications of the notions of forcing and generic sets. Fundamenta Mathematicae, vol. 56 (1964), pp. 325–345.10.4064/fm-56-3-325-345CrossRefGoogle Scholar
Grigorieff, S., Intermediate submodels and generic extensions in set theory. Annals of Mathematics(2), vol. 101 (1975), pp. 447–490.10.2307/1970935CrossRefGoogle Scholar
Halpern, J. D. and Lévy, A., The Boolean prime ideal theorem does not imply the axiom of choice, Axiomatic Set Theory (Scott, D., editor), Proceedings of Symposia in Pure Mathematics, vol. XIII, part I, American Mathematical Society, Providence, RI, 1971, pp. 83–134.10.1090/pspum/013.1/0284328CrossRefGoogle Scholar
Jech, T., Set Theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Jech, T. J., The Axiom of Choice, Studies in Logic and the Foundations of Mathematics, Vol. 75, North-Holland, Amsterdam, 1973.Google Scholar
Karagila, A., The Bristol model: An abyss called a Cohen real. Journal of Mathematical Logic, vol. 18 (2018), no. 2, 1850008.10.1142/S0219061318500083CrossRefGoogle Scholar
Kinna, W. and Wagner, K., Über eine Abschwächung des Auswahlpostulates. Fundamenta Mathematicae, vol. 42 (1955), pp. 75–82.10.4064/fm-42-1-75-82CrossRefGoogle Scholar
Monro, G. P., Models of ZF with the same sets of sets of ordinals. Fundamenta Mathematicae , vol. 80 (1973), no. 2, pp. 105–110.10.4064/fm-80-2-105-110CrossRefGoogle Scholar
Pincus, D., The dense linear ordering principle, this Journal, vol. 62 (1997), no. 2, pp. 438–456.Google Scholar
Sageev, G., An independence result concerning the axiom of choice. Annals of Mathematical Logic, vol. 8 (1975), pp. 1–184.10.1016/0003-4843(75)90002-9CrossRefGoogle Scholar
Sageev, G., A model of ZF+ there exists an inaccessible, in which the Dedekind cardinals constitute a natural nonstandard model of arithmetic. Annals of Mathematical Logic, vol. 21 (1981), no. 2–3, pp. 221–281.10.1016/0003-4843(81)90017-6CrossRefGoogle Scholar
Shani, A., Borel reducibility and symmetric models, preprint, 2018, arXiv:1810.06722.Google Scholar