Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cholak, Peter
and
Harrington, Leo
2007.
Extension theorems, orbits, and automorphisms of the computably enumerable sets.
Transactions of the American Mathematical Society,
Vol. 360,
Issue. 4,
p.
1759.
Cholak, Peter
Downey, Rodney
and
Harrington, Leo
2008.
On the orbits of computably enumerable sets.
Journal of the American Mathematical Society,
Vol. 21,
Issue. 4,
p.
1105.
Cholak, Peter A.
Downey, Rodney
and
Harrington, Leo A.
2008.
The Complexity of Orbits of Computably Enumerable Sets.
Bulletin of Symbolic Logic,
Vol. 14,
Issue. 1,
p.
69.
Lavrov, I. A.
2012.
Computably enumerable sets and related issues.
Algebra and Logic,
Vol. 50,
Issue. 6,
p.
494.
Cholak, Peter A.
2017.
The Incomputable.
p.
83.


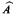 are automorphic via Φ then the structures
are automorphic via Φ then the structures 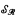 (
(