No CrossRef data available.
Article contents
Interpreting true arithmetic in the 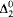 -enumeration degrees
-enumeration degrees
Published online by Cambridge University Press: 12 March 2014
Abstract
We show that there is a first order sentence φ(x: a, b, l) such that for every computable partial order 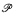 and
and 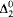 -degree u > 0e, there are
-degree u > 0e, there are 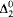 -enumeration degrees a ≤ u, b, and l such that
-enumeration degrees a ≤ u, b, and l such that 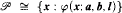 . Allowing
. Allowing 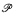 to be a suitably defined standard model of arithmetic gives a parameterized interpretation of true arithmetic in the
to be a suitably defined standard model of arithmetic gives a parameterized interpretation of true arithmetic in the 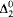 -enumeration degrees. Finally we show that there is a first order sentence that correctly identifies a subset of the standard models, which gives a parameterless interpretation of true arithmetic in the
-enumeration degrees. Finally we show that there is a first order sentence that correctly identifies a subset of the standard models, which gives a parameterless interpretation of true arithmetic in the 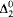 -enumeration degrees.
-enumeration degrees.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2010


