Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T20:47:57.487Z Has data issue: false hasContentIssue false
  • English
  • Français

INTEGRATION AND CELL DECOMPOSITION IN P-MINIMAL STRUCTURES

Published online by Cambridge University Press:  18 July 2016

PABLO CUBIDES KOVACSICS  and
EVA LEENKNEGT
PABLO CUBIDES KOVACSICS
Affiliation:
LABORATOIRE PAUL PAINLEVÉUNIVERSITÉ DE LILLE 1CNRS U.M.R. 852459655 VILLENEUVE D’ASCQ CEDEX FRANCEE-mail: [email protected]
EVA LEENKNEGT
Affiliation:
DEPARTMENT OF MATHEMATICS KULEUVEN CELESTIJNENLAAN 200B3001 HEVERLEE BELGIUME-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the class of ${\cal L}$-constructible functions is closed under integration for any P-minimal expansion of a p-adic field 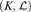$\left( {K,{\cal L}} \right)$. This generalizes results previously known for semi-algebraic and subanalytic structures. As part of the proof, we obtain a weak version of cell decomposition and function preparation for P-minimal structures, a result which is independent of the existence of Skolem functions. A direct corollary is that Denef’s results on the rationality of Poincaré series hold in any P-minimal expansion of a p-adic field 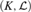$\left( {K,{\cal L}} \right)$.

Keywords

P-minimalityp-adic numbersp-adic cell decompositionconstructible functionsfunction preparationintegrationrationality of Poincaré series
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 3 , September 2016 , pp. 1124 - 1141
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Cluckers, R., Analytic p-adic cell decomposition and integrals . Transactions of the American Mathematical Society, vol. 356 (2003), no. 4, pp. 1489–1499.Google Scholar
Cluckers, R., Presburger sets and p-minimal fields , this Journal, vol. 68 (2003), no. 1, pp. 153–162.Google Scholar
Cluckers, R. and Leenknegt, E., A version of p-adic minimality , this Journal, vol. 77 (2012), no. 2, pp. 621–630.Google Scholar
Cluckers, R. and Lipshitz, L., Fields with analytic structure . Journal of the European Mathematical Society, vol. 13 (2011), pp. 1147–1223.Google Scholar
Cluckers, R., Classification of semi-algebraic p-adic sets up to semi-algebraic bijection . Journal für die Reine und Angewandte Mathematik, vol. 540 (2001), pp. 105–114.Google Scholar
Cluckers, R., Gordon, J., and Halupczok, I., Integrability of oscillatory functions on local fields: transfer principles . Duke Mathematical Journal, vol. 163 (2014), no. 8, pp. 1549–1600.Google Scholar
Darniere, L., Cell decomposition and dimension theory on p-optimal fields, arXiv:1412.2571v2, 2015.Google Scholar
Denef, J., The rationality of the Poincaré series associated to the p-adic points on a variety . Inventiones Mathematicae, vol. 77 (1984), pp. 1–23.Google Scholar
Denef, J., On the evaluation of certain p-adic integrals , Séminaire de théorie des nombres, Paris 1983–84, Progress in Mathematics, vol. 59, Birkhäuser Boston, Boston, MA, 1985, pp. 25–47.Google Scholar
Denef, J., Arithmetic and geometric applications of quantifier elimination for valued fields , Model Theory, Algebra, and Geometry, Mathematical Sciences Research Institute Publications, vol. 39, Cambridge University Press, Cambridge, 2000, pp. 173–198.Google Scholar
Denef, J. and van den Dries, L., p-adic and real subanalytic sets . Annals of Mathematics (2), vol. 128 (1988), no. 1, pp. 79–138.Google Scholar
Denef, J., p-adic semi-algebraic sets and cell decomposition . Journal für die Reine und Angewandte Mathematik, vol. 369 (1986), pp. 154–166.Google Scholar
Haskell, D. and Macpherson, D., A version of o-minimality for the p-adics , this Journal, vol. 62 (1997), no. 4, pp. 1075–1092.Google Scholar
Hodges, W., A Shorter Model Theory, Cambridge University Press, New York, NY, 1997.Google Scholar
Igusa, J.-I., Complex powers and asymptotic expansions. I. Functions of certain types . Journal für die Reine und Angewandte Mathematik, vol. 268/269 (1974), pp. 110–130. Collection of articles dedicated to Helmut Hasse on his seventy-fifth birthday, II.Google Scholar
Igusa, J.-I., Complex powers and asymptotic expansions. II. Asymptotic expansions . Journal für die Reine und Angewandte Mathematik, vol. 278/279 (1975), pp. 307–321.Google Scholar
Igusa, J.-I., Forms of Higher Degree, Tata Institute of Fundamental Research Lectures on Mathematics and Physics, vol. 59, Tata Institute of Fundamental Research, Bombay, 1978. Published by Narosa Publishing House, New Delhi.Google Scholar
Leenknegt, E., Reducts of p-adically closed fields . Archive for Mathematical Logic, vol. 53 (2014), no. 3–4, pp. 285–306.Google Scholar
Macintyre, A., On definable subsets of p-adic fields , this Journal, vol. 41 (1976), pp. 605–610.Google Scholar
Mourgues, M.-H., Cell decomposition for P-minimal fields . Mathematical Logic Quarterly, vol. 55 (2009), no. 5, pp. 487–492.Google Scholar
Point, F. and Wagner, F. O., Essentially periodic ordered groups . Annals of Pure and Applied Logic, vol. 105 (2000), no. 1–3, pp. 261–291.CrossRefGoogle Scholar
Ramakrishnan, J., Definable linear orders definably embed into lexicographic orders in o-minimal structures . Proceedings of the American Mathematical Society, vol. 141 (2013), no. 5, pp. 1809–1819.Google Scholar
van den Dries, L., Tame Topology and O-minimal Structures, London Mathematical Society Lecture Note Series, vol. 248, Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar