Article contents
INITIAL SELF-EMBEDDINGS OF MODELS OF SET THEORY
Published online by Cambridge University Press: 13 August 2021
Abstract
By a classical theorem of Harvey Friedman (1973), every countable nonstandard model  $\mathcal {M}$
of a sufficiently strong fragment of ZF has a proper rank-initial self-embedding j, i.e., j is a self-embedding of
$\mathcal {M}$
of a sufficiently strong fragment of ZF has a proper rank-initial self-embedding j, i.e., j is a self-embedding of  $\mathcal {M}$
such that
$\mathcal {M}$
such that 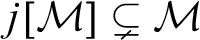 $j[\mathcal {M}]\subsetneq \mathcal {M}$
, and the ordinal rank of each member of
$j[\mathcal {M}]\subsetneq \mathcal {M}$
, and the ordinal rank of each member of 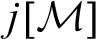 $j[\mathcal {M}]$
is less than the ordinal rank of each element of
$j[\mathcal {M}]$
is less than the ordinal rank of each element of 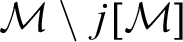 $\mathcal {M}\setminus j[\mathcal {M}]$
. Here, we investigate the larger family of proper initial-embeddings j of models
$\mathcal {M}\setminus j[\mathcal {M}]$
. Here, we investigate the larger family of proper initial-embeddings j of models  $\mathcal {M}$
of fragments of set theory, where the image of j is a transitive submodel of
$\mathcal {M}$
of fragments of set theory, where the image of j is a transitive submodel of  $\mathcal {M}$
. Our results include the following three theorems. In what follows,
$\mathcal {M}$
. Our results include the following three theorems. In what follows,  $\mathrm {ZF}^-$
is
$\mathrm {ZF}^-$
is  $\mathrm {ZF}$
without the power set axiom;
$\mathrm {ZF}$
without the power set axiom; 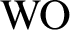 $\mathrm {WO}$
is the axiom stating that every set can be well-ordered;
$\mathrm {WO}$
is the axiom stating that every set can be well-ordered; 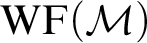 $\mathrm {WF}(\mathcal {M})$
is the well-founded part of
$\mathrm {WF}(\mathcal {M})$
is the well-founded part of  $\mathcal {M}$
; and
$\mathcal {M}$
; and 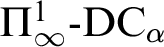 $\Pi ^1_\infty \text{-}\mathrm {DC}_\alpha $
is the full scheme of dependent choice of length
$\Pi ^1_\infty \text{-}\mathrm {DC}_\alpha $
is the full scheme of dependent choice of length 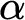 $\alpha $
.
$\alpha $
.
Theorem A.
There is an 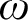 $\omega $
-standard countable nonstandard model
$\omega $
-standard countable nonstandard model  $\mathcal {M}$
of
$\mathcal {M}$
of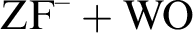 $\mathrm {ZF}^-+\mathrm {WO}$
that carries no initial self-embedding
$\mathrm {ZF}^-+\mathrm {WO}$
that carries no initial self-embedding 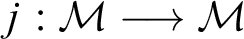 $j:\mathcal {M} \longrightarrow \mathcal {M}$
other than the identity embedding.
$j:\mathcal {M} \longrightarrow \mathcal {M}$
other than the identity embedding.
Theorem B.
Every countable 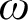 $\omega $
-nonstandard model
$\omega $
-nonstandard model  $\mathcal {M}$
of
$\mathcal {M}$
of  $\ \mathrm {ZF}$
is isomorphic to a transitive submodel of the hereditarily countable sets of its own constructible universe
$\ \mathrm {ZF}$
is isomorphic to a transitive submodel of the hereditarily countable sets of its own constructible universe 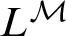 $L^{\mathcal {M}}$
.
$L^{\mathcal {M}}$
.
Theorem C.
The following three conditions are equivalent for a countable nonstandard model  $\mathcal {M}$
of
$\mathcal {M}$
of 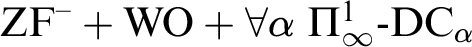 $\mathrm {ZF}^{-}+\mathrm {WO}+\forall \alpha \ \Pi ^1_\infty \text{-}\mathrm {DC}_\alpha $
.
$\mathrm {ZF}^{-}+\mathrm {WO}+\forall \alpha \ \Pi ^1_\infty \text{-}\mathrm {DC}_\alpha $
.
(I) There is a cardinal in
 $\mathcal {M}$
that is a strict upper bound for the cardinality of each member of
$\mathcal {M}$
that is a strict upper bound for the cardinality of each member of 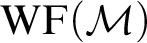 $\mathrm {WF}(\mathcal {M})$
.
$\mathrm {WF}(\mathcal {M})$
.(II)
 $\mathrm {WF}(\mathcal {M})$
satisfies the powerset axiom.
$\mathrm {WF}(\mathcal {M})$
satisfies the powerset axiom.(III) For all
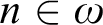 $n \in \omega $
and for all
$n \in \omega $
and for all 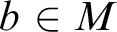 $b \in M$
, there exists a proper initial self-embedding
$b \in M$
, there exists a proper initial self-embedding 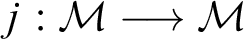 $j: \mathcal {M} \longrightarrow \mathcal {M}$
such that
$j: \mathcal {M} \longrightarrow \mathcal {M}$
such that 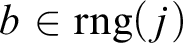 $b \in \mathrm {rng}(j)$
and
$b \in \mathrm {rng}(j)$
and  $j[\mathcal {M}] \prec _n \mathcal {M}$
.
$j[\mathcal {M}] \prec _n \mathcal {M}$
.
MSC classification
- Type
- Article
- Information
- Copyright
- © Association for Symbolic Logic 2021
References
- 1
- Cited by



