Article contents
Initial segments of the lattice of ideals of r.e. degrees
Published online by Cambridge University Press: 12 March 2014
Extract
Embeddings into initial segments of 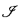 (the lattice of ideals of r.e. degrees) are relevant for the investigation of decidability of (fragments of) the theory of
(the lattice of ideals of r.e. degrees) are relevant for the investigation of decidability of (fragments of) the theory of 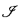 (with constant-symbols denoting principal ideals). Interest in this investigation stems from open problems concerning decidability of fragments of the theory of R (the usl of r.e. degrees) and embeddings into R. Ambos-Spies and Lerman established comprehensive nonembeddability [AS/LR1] and embeddability [AS/LR2] conditions, but their complementarity is open. (For background on embeddings and decidability consult Lerman [LR1] and Lerman and Shore [LR/SH].) The first systematic investigation of embeddings into
(with constant-symbols denoting principal ideals). Interest in this investigation stems from open problems concerning decidability of fragments of the theory of R (the usl of r.e. degrees) and embeddings into R. Ambos-Spies and Lerman established comprehensive nonembeddability [AS/LR1] and embeddability [AS/LR2] conditions, but their complementarity is open. (For background on embeddings and decidability consult Lerman [LR1] and Lerman and Shore [LR/SH].) The first systematic investigation of embeddings into 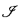 is in Calhoun [CL], where the existence of uniform bounds, in the case of embeddings into
is in Calhoun [CL], where the existence of uniform bounds, in the case of embeddings into 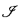 , on the number of “join traces” arising with nondistributive lattices is shown to remove “obstructions” to lattice-embeddings into R (such as typified in the nonembeddable lattice S8, see [LA/SR], [AS/LR1/). The analysis to follow extends this, by showing that it also removes the “obstruction” to lattice-embeddings into initial segments of R, arising with Lachlan's M5, which embeds into R, but not into every nontrivial initial segment R[0, a], by a result of Downey [DW]. The techniques are Lachlan's [LA], as adapted in Lerman's “pinball machine model” [LR1, LR2], combined with Fejer's “meet-trick” [FJ] as used by Downey [DW] in the proof that every distributive lattice is embeddable into every nontrivial initial segment of r.e. degrees R[0, a], a > 0. We present a sufficient condition, “allowing evasion” [Definition 4.2] for lattice embeddability into every
, on the number of “join traces” arising with nondistributive lattices is shown to remove “obstructions” to lattice-embeddings into R (such as typified in the nonembeddable lattice S8, see [LA/SR], [AS/LR1/). The analysis to follow extends this, by showing that it also removes the “obstruction” to lattice-embeddings into initial segments of R, arising with Lachlan's M5, which embeds into R, but not into every nontrivial initial segment R[0, a], by a result of Downey [DW]. The techniques are Lachlan's [LA], as adapted in Lerman's “pinball machine model” [LR1, LR2], combined with Fejer's “meet-trick” [FJ] as used by Downey [DW] in the proof that every distributive lattice is embeddable into every nontrivial initial segment of r.e. degrees R[0, a], a > 0. We present a sufficient condition, “allowing evasion” [Definition 4.2] for lattice embeddability into every 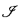 [0, a], a > 0.
[0, a], a > 0.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1994
References
REFERENCES
- 1
- Cited by


