Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Taylor, Walter
1973.
A heterogeneous interpolant.
Nagoya Mathematical Journal,
Vol. 52,
Issue. ,
p.
31.
Friedman, Harvey
1973.
Beth’s theorem in cardinality logics.
Israel Journal of Mathematics,
Vol. 14,
Issue. 2,
p.
205.
Kueker, David W.
1975.
Infinitary Logic: In Memoriam Carol Karp.
Vol. 492,
Issue. ,
p.
17.
1975.
Large Infinitary Languages - Model Theory.
Vol. 83,
Issue. ,
p.
438.
Hutchinson, John E.
1976.
Model theory via set theory.
Israel Journal of Mathematics,
Vol. 24,
Issue. 3-4,
p.
286.
Kueker, David W.
1977.
Countable approximations and Löwenheim-Skolem theorems.
Annals of Mathematical Logic,
Vol. 11,
Issue. 1,
p.
57.
Makkai, M.
1977.
HANDBOOK OF MATHEMATICAL LOGIC.
Vol. 90,
Issue. ,
p.
233.
Barwise, Jon
Kaufmann, Matt
and
Makkai, Michael
1978.
Stationary logic.
Annals of Mathematical Logic,
Vol. 13,
Issue. 2,
p.
171.
Kueker, David W.
1978.
Logic Colloquium '77.
Vol. 96,
Issue. ,
p.
161.
Makowsky, J. A.
and
Shelah, S.
1979.
The theorems of Beth and Craig in abstract model theory. I. The abstract setting.
Transactions of the American Mathematical Society,
Vol. 256,
Issue. 0,
p.
215.
Mundici, Daniele
1982.
Compactness, interpolation and Friedman's third problem.
Annals of Mathematical Logic,
Vol. 22,
Issue. 2,
p.
197.
Oikkonen, Juha
1987.
Logic Colloquium '86, Proceedings of the Colloquium held in Hull.
Vol. 124,
Issue. ,
p.
175.
Caicedo, Xavier
2004.
Definability and automorphisms in abstract logics.
Archive for Mathematical Logic,
Vol. 43,
Issue. 8,
p.
937.
Makowsky, J.A.
2004.
Algorithmic uses of the Feferman–Vaught Theorem.
Annals of Pure and Applied Logic,
Vol. 126,
Issue. 1-3,
p.
159.
Väänänen, Jouko
2008.
The Craig Interpolation Theorem in abstract model theory.
Synthese,
Vol. 164,
Issue. 3,
p.
401.
DŽAMONJA, MIRNA
and
VÄÄNÄNEN, JOUKO
2011.
CHAIN MODELS, TREES OF SINGULAR CARDINALITY AND DYNAMIC EF-GAMES.
Journal of Mathematical Logic,
Vol. 11,
Issue. 01,
p.
61.
KENNEDY, JULIETTE
and
VÄÄNÄNEN, JOUKO
2021.
LOGICALITY AND MODEL CLASSES.
The Bulletin of Symbolic Logic,
Vol. 27,
Issue. 4,
p.
385.
HARRISON-TRAINOR, MATTHEW
and
KRETSCHMER, MILES
2024.
INFINITARY LOGIC HAS NO EXPRESSIVE EFFICIENCY OVER FINITARY LOGIC.
The Journal of Symbolic Logic,
Vol. 89,
Issue. 4,
p.
1817.
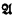 i, and
i, and 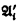 , have the same true Lω, ω sentences (i.e., are elementarily equivalent) for i = 1, 2, then the cardinal sums
, have the same true Lω, ω sentences (i.e., are elementarily equivalent) for i = 1, 2, then the cardinal sums 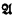 1 +
1 + 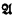 2 and
2 and 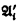 +
+ 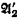 have the same true Lω, ω sentences, and the direct products
have the same true Lω, ω sentences, and the direct products 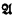 1 ·
1 · 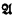 2 and
2 and 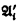 ·
· 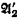 have the same true Lω, ω sentences [3]. We show that this is true when ‘Lω, ω’ is replaced by ‘Lκ, λ’ if and only if κ is strongly inaccessible. For Lω1, ω this settles a question, posed by Lopez-Escobar [7].
have the same true Lω, ω sentences [3]. We show that this is true when ‘Lω, ω’ is replaced by ‘Lκ, λ’ if and only if κ is strongly inaccessible. For Lω1, ω this settles a question, posed by Lopez-Escobar [7].

