No CrossRef data available.
Article contents
The inconsistency of a certain axiom system for set theory
Published online by Cambridge University Press: 12 March 2014
Extract
We prove in this paper that the 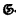 -system, an axiom system for set theory suggested for investigation by Takeuti in [2], is inconsistent. We also show that this system without the ω-rule is consistent if Zermelo-Fraenkel set theory with the axiom of choice and an axiom due to Reinhardt and Silver is consistent. The
-system, an axiom system for set theory suggested for investigation by Takeuti in [2], is inconsistent. We also show that this system without the ω-rule is consistent if Zermelo-Fraenkel set theory with the axiom of choice and an axiom due to Reinhardt and Silver is consistent. The 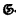 -system is an effort to strengthen Bernays-Gödel set theory by adding a reflection principle.
-system is an effort to strengthen Bernays-Gödel set theory by adding a reflection principle.
In addition to the standard notation of set theory, we write X″{x) to mean {y∣〈x, y〉 Є X}.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972


