Article contents
Implicational complexity in intuitionistic arithmetic
Published online by Cambridge University Press: 12 March 2014
Extract
In classical arithmetic a natural measure for the complexity of relations is provided by the number of quantifier alternations in an equivalent prenex normal form. However, the proof of the Prenex Normal Form Theorem uses the following intuitionistically invalid rules for permuting quantifiers with propositional constants.
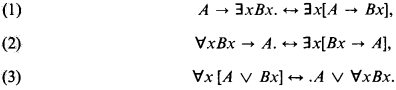
Each one of these schemas, when added to Intuitionistic (Heyting's) Arithmetic IA, generates full Classical (Peano's) Arithmetic. Schema (3) is of little interest here, since one can obtain a formula intuitionistically equivalent to A ∨ ∀xBx, which is prenex if A and B are:
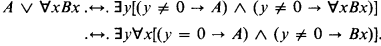
For the two conjuncts on the r.h.s. (1) may be successively applied, since y = 0 is decidable.
We shall readily verify that there is no way of similarly going around (1) or (2). This fact calls for counting implication (though not conjunction or disjunction) in measuring in IA the complexity of arithmetic relations. The natural implicational measure for our purpose is the depth of negative nestings of implication, defined as follows. I(F): = 0 if F is atomic; I(F ∧ G) = I(F ∨ G): = max[I(F), I(G)]; I(∀xF) = I(∃xF): = I(F); I(F → G):= max[I(F) + 1, I(G)].
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1981
References
REFERENCES
- 5
- Cited by


