Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-04T09:32:33.310Z Has data issue: false hasContentIssue false
  • English
  • Français

Ideographic computation in the propositional calculus

Published online by Cambridge University Press:  12 March 2014

Gerald B. Standley
Gerald B. Standley*
Affiliation:
St. Lawrence University
Get access Rights & Permissions [Opens in a new window]

Extract

This paper will be concerned with an adaptation of Parry's trapezoid symbolism to the solving of problems.

In Parry's notation ‘p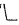q’, in particular, sets forth the relationship that obtains when p is true, whether q be true or false. The symbol may also be regarded as manifesting the matrix analysis of p. It is this aspect which offers promise for manipulation. We propose to write the symbol ‘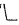’ for p itself. It is to be kept in mind, however, that ‘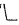’ is the symbol of p when there are but two variables. How to proceed when there are more than two will be seen later.

The symbol for q will in like manner be ‘⌋’.

Let ‘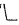’ and ‘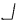’, then, be regarded as elemental symbols setting forth the matrix analysis of the variables. Suppose further that in transcribing from conventional to the trapezoid symbolism we substitute for the variables only, retaining the constants (antithetically to Parry's procedure). Thus ‘p ∨ q’ becomes, not ‘p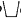q’ as with Parry, but ‘ 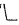∨ 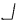’. Problem-solving consists of merging the trapezoidal symbols according to procedures specified by the constants. As symbols are merged, the constants are eliminated.

The resultant symbol constitutes the solution.

The rules for merging symbols are derived from the elementary processes of forming truth-tables:

Disjunction of two symbols consists of superimposing them.

Conjunction consists of preserving only such sides as are common to both the conjoined symbols.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 19 , Issue 3 , September 1954 , pp. 169 - 171
Copyright
Copyright © Association for Symbolic Logic 1954

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 As set forth in his paper in this Journal, vol. 19 (1953), pp. 161–168.

2 I.e., ‘p⊃q’ is treated as .

3 One trapezoidal expression implies another if the antecedent can be contained in the consequent.

4 Quine, Willard Van Orman, Methods of logic, (New York, 1950), p. 30Google Scholar.

5 Where the conjunction contains no explicit p, q function, it may be treated as conjoined to (cf. line 6 of the second example).