Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T01:45:21.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Hyper-regular lattice-ordered groups

Published online by Cambridge University Press:  12 March 2014

Daniel Gluschankof  and
François Lucas
Daniel Gluschankof
Affiliation:
Equipe de Logique Mathématique, UFR de Mathématiques, Université Paris 7, CNRS (URA 753) 75251 Paris Cedex 05, France, E-mail [email protected], [email protected]
François Lucas
Affiliation:
Département de Mathématiques, Université d'Angers, 49045 Angers Cedex, France, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

It is a well-known fact that the notion of an archimedean order cannot be formalized in the first-order calculus. In [12] and [18], A. Robinson and E. Zakon characterized the elementary class generated by all the archimedean, totally-ordered abelian groups (o-groups) in the language 〈+,<〉, calling it the class of regularly ordered or generalized archimedean abelian groups. Since difference (−) and 0 are definable in that language, it is immediate that in the expanded language 〈 +, −, 0, < 〉 the definable expansion of the class of regular groups is also the elementary class generated by the archimedean ones. In the more general context of lattice-ordered groups (l-groups), the notion of being archimedean splits into two different notions: a strong one (being hyperarchimedean) and a weak one (being archimedean). Using the representation theorem of K. Keimel for hyperarchimedean l-groups, we extend in this paper the Robinson and Zakon characterization to the elementary class generated by the prime-projectable, hyperarchimedean l-groups. This characterization is also extended here to the elementary class generated by the prime-projectable and projectable archimedean l-groups (including all complete l-groups). Finally, transferring a result of A. Touraille on the model theory of Boolean algebras with distinguished ideals, we give the classification up to elementary equivalence of the characterized class.

We recall that a lattice-ordered group, l-group for short, is a structure

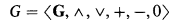
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 58 , Issue 4 , December 1993 , pp. 1342 - 1358
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bigard, A., Keimel, K. and Wolfenstein, S., Groupes et anneaux réticulés, Lecture Notes in Mathematics, vol. 608, Springer-Verlag, Berlin and New York, 1977.CrossRefGoogle Scholar
[2]Burris, S. and Sankappanavar, H. P., A course in universal algebra, Springer-Verlag, New York, Heidelberg, and Berlin, 1981.CrossRefGoogle Scholar
[3]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[4]Comer, S., Elementary properties of structures of sections, Boletin Sociedad Matemática Mexicana, vol. 19 (1974), pp. 78–85.Google Scholar
[5]Ebinghaus, H. D., Flum, J. and Thomas, W., Mathematical logic, Springer-Verlag, New York, 1984.Google Scholar
[6]Gluschankof, D., The first order theory of products of totally ordered abelian groups, this Journal, vol. 56 (1991), pp. 295–299.Google Scholar
[7]Gurevich, Yu., Elementary properties of ordered abelian groups, Translations of the American Mathematical Society, vol. 49, Amer. Math. Soc, Providence, RI, 1965, pp. 165–192.Google Scholar
[8]Hodges, W. A., Constructing models by games, Cambridge University Press, Cambridge, 1985.Google Scholar
[9]Keimel, K., The representation of lattice-ordered groups and rings by sections of sheaves, Lecture Notes in Mathematics, vol. 248, Springer-Verlag, Berlin and New York, 1972, pp. 1–72.Google Scholar
[10]Point, F., Quantifier elimination for projectable L-groups and linear elimination for f-rings, Ph.D. Thesis, Université de l'Etat à Mons, Mons, Belgium, 1983.Google Scholar
[11]Poizat, B., Cours de Théorie des Modèles, Nur al-Mantiq wal-ma'rifah, Paris, 1985.Google Scholar
[12]Robinson, A. and Zakon, E., Elementary properties of ordered abelian groups, Transactions of the American Mathematical Society, vol. 96, Amer. Math. Soc, Providence, RI, 1960, pp. 222–236.Google Scholar
[13]Touraille, A., Théories d'algèbres de Boole munies d'idéaux distingués I, this Journal, vol. 52 (1987), pp. 1027–1043.Google Scholar
[14]Touraille, A., Théories d'algèbres de Boole munies d'idéaux distingués II, this Journal, vol. 55 (1990), pp. 1192–1212.Google Scholar
[15]Weispfenning, V., Model-Completeness and elimination of quantifiers for subdirect products of structures, Journal of Algebra, vol. 36 (1975), pp. 252–277.CrossRefGoogle Scholar
[16]Weispfenning, V., Model theory of lattice-products, Habilitationschrift, Ruprecht-Karl-Universität, Heidelberg, 1978.Google Scholar
[17]Weispfenning, V., Elimination of quantifiers for certain ordered and lattice-ordered abelian groups, Bulletin de la Société Mathématique de Belgique. Série B, vol. XXXIII (1981), pp. 131–155.Google Scholar
[18]Zakon, E., Generalized archimedean groups, Transactions of the American Mathematical Society, vol. 99 (1961), pp. 21–40.CrossRefGoogle Scholar