Article contents
Hypergraph sequences as a tool for saturation of ultrapowers
Published online by Cambridge University Press: 12 March 2014
Abstract
Let T1, T2 be countable first-order theories, Mi ⊨ Ti and 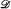 any regular ultrafilter on λ ≥ ℵ0. A longstanding open problem of Keisler asks when T2 is more complex than T1, as measured by the fact that for any such λ,
any regular ultrafilter on λ ≥ ℵ0. A longstanding open problem of Keisler asks when T2 is more complex than T1, as measured by the fact that for any such λ, 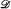 , if the ultrapower
, if the ultrapower 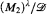 realizes all types over sets of size ≤ λ, then so must the ultrapower
realizes all types over sets of size ≤ λ, then so must the ultrapower  . In this paper, building on the author's prior work [12] [13] [14], we show that the relative complexity of first-order theories in Keisler's sense is reflected in the relative graph-theoretic complexity of sequences of hypergraphs associated to formulas of the theory. After reviewing prior work on Keisler's order, we present the new construction in the context of ultrapowers, give various applications to the open question of the unstable classification, and investigate the interaction between theories and regularizing sets. We show that there is a minimum unstable theory, a minimum TP2 theory, and that maximality is implied by the density of certain graph edges (between components arising from Szemerédi-regular decompositions) remaining bounded away from 0, 1. We also introduce and discuss flexible ultrafilters, a relevant class of regular ultrafilters which reflect the sensitivity of certain unstable (non low) theories to the sizes of regularizing sets, and prove that any ultrafilter which saturates the minimal TP2 theory is flexible.
. In this paper, building on the author's prior work [12] [13] [14], we show that the relative complexity of first-order theories in Keisler's sense is reflected in the relative graph-theoretic complexity of sequences of hypergraphs associated to formulas of the theory. After reviewing prior work on Keisler's order, we present the new construction in the context of ultrapowers, give various applications to the open question of the unstable classification, and investigate the interaction between theories and regularizing sets. We show that there is a minimum unstable theory, a minimum TP2 theory, and that maximality is implied by the density of certain graph edges (between components arising from Szemerédi-regular decompositions) remaining bounded away from 0, 1. We also introduce and discuss flexible ultrafilters, a relevant class of regular ultrafilters which reflect the sensitivity of certain unstable (non low) theories to the sizes of regularizing sets, and prove that any ultrafilter which saturates the minimal TP2 theory is flexible.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2012
References
REFERENCES
- 15
- Cited by


