Article contents
A hierarchy of tree-automatic structures
Published online by Cambridge University Press: 12 March 2014
Abstract
We consider ωn-automatic structures which are relational structures whose domain and relations are accepted by automata reading ordinal words of length ωn for some integer n ≥ 1. We show that all these structures are ω-tree-automatic structures presentable by Muller or Rabin tree automata. We prove that the isomorphism relation for ω2-automatic (resp. ωn-automatic for n > 2) boolean algebras (respectively, partial orders, rings, commutative rings, non commutative rings, non commutative groups) is not determined by the axiomatic system ZFC. We infer from the proof of the above result that the isomorphism problem for ωn-automatic boolean algebras, n ≥ 2, (respectively, rings, commutative rings, non commutative rings, non commutative groups) is neither a 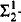 -set nor a
-set nor a 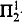 -set. We obtain that there exist infinitely many ωn-automatic, hence also ω-tree-automatic, atomless boolean algebras
-set. We obtain that there exist infinitely many ωn-automatic, hence also ω-tree-automatic, atomless boolean algebras 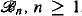 , which are pairwise isomorphic under the continuum hypothesis CH and pairwise non isomorphic under an alternate axiom AT, strengthening a result of [14].
, which are pairwise isomorphic under the continuum hypothesis CH and pairwise non isomorphic under an alternate axiom AT, strengthening a result of [14].
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2012
References
REFERENCES
- 5
- Cited by


