Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-13T15:04:30.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Hierarchies of forcing axioms I

Published online by Cambridge University Press:  12 March 2014

Itay Neeman  and
Ernest Schimmerling
Itay Neeman
Affiliation:
University of California at los Angeles, Department of Mathematics, Los Angeles, Ca 90095-1555, USA, E-mail: [email protected]
Ernest Schimmerling
Affiliation:
Carnegie Mellon University, Department of Mathematical Sciences, Pittsburgh, PA 15213-3890, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove new upper bound theorems on the consistency strengths of SPFA(θ), SPFA(θ-linked) and SPFA(θ+ -cc). Our results are in terms of (θ, Γ)-subcompactness, which is a new large cardinal notion that combines the ideas behind subcompactness and Γ-indescribability. Our upper bound for SPFA(ϲ-linked) has a corresponding lower bound, which is due to Neeman and appears in his follow-up to this paper. As a corollary, SPFA(ϲ-linked) and PFA(ϲ-linked) are each equiconsistent with the existence of a 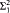-indescribable cardinal. Our upper bound for SPFA(ϲ-c.c) is a 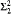-indescribable cardinal, which is consistent with V = L. Our upper bound for SPFA(ϲ+-linked) is a cardinals κ that is (κ+,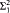)-subcompact, which is strictly weaker than κ+-supercompact. The axiom MM(ϲ) is a consequence of SPFA(ϲ+-linked) by a slight refinement of a theorem of Shelah. Our upper bound for SPFA(ϲ++-c.c.) is a cardinal κ that is (κ+, 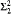)-subcompact, which is also strictly weaker than κ+-supercompact.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 1 , March 2008 , pp. 343 - 362
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baumgartner, James E., Iterated forcing, Surveys in Set Theory, London Mathematical Society Lecture Note Series, vol. 87, Cambridge University Press, 1983, pp. 1–59.Google Scholar
[2]Bekkali, M., Topics in Set Theory: Lebesgue measurability, large cardinals, forcing axioms, rho-functions, Lecture Notes in Mathematics, vol. 1476, Springer-Verlag, Berlin, 1991, notes on lectures by Stevo Todorčević.CrossRefGoogle Scholar
[3]Burke, Douglas, Generic embeddings and the failure of box, Proceedings of the American Mathematical Society, vol. 123 (1995), no. 9, pp. 2867–2871.CrossRefGoogle Scholar
[4]Donder, Dieter and Fuchs, Ulrich, Revised countable support iterations, preprint.Google Scholar
[5]Foreman, M., Magidor, M., and Shelah, S., Martin's maximum, saturated ideals, and nonregular ultrafilters, Part I, Annals of Mathematics (2), vol. 127 (1988), no. 1, pp. 1–47.CrossRefGoogle Scholar
[6]Hamkins, Joel David, The lottery preparation, Annals of Pure and Applied Logic, vol. 101 (2000), no. 2-3, pp. 103–146.CrossRefGoogle Scholar
[7]Jech, T., Multiple forcing, Cambridge Tracts in Mathematics, vol. 88, Cambridge University Pres, Cambridge, 1986.Google Scholar
[8]Neeman, Itay, Hierarchies of forcing axioms II, this Journal, to appear.Google Scholar
[9]Schimmerling, Ernest, Coherent sequences and threads, Advances in Mathematics, vol. 216 (2007), no. 1, pp. 89–117.CrossRefGoogle Scholar
[10]Schimmerling, Ernest and Zeman, Martin, Square in core models, The Bulletin of Symbolic Logic, vol. 7 (2001), no. 3, pp. 305–314.CrossRefGoogle Scholar
[11]Shelah, Saharon, Semiproper forcing axiom implies Martin maximum but not PFA+, this Journal, vol. 52 (1987), no. 2, pp. 360–367.Google Scholar
[12]Shelah, Saharon, Proper and Improper Forcing, 2nd ed., Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1998.CrossRefGoogle Scholar
[13]Todorčević, Stevo, A note on the proper forcing axiom, Axiomatic Set Theory (Boulder, Colorado, 1983), Contemporary Mathematics, vol. 31, American Mathematical Society, Providence, RI, 1984, pp. 209–218.CrossRefGoogle Scholar
[14]Veličković, Boban, Jensen's □ principles and the Novak number of partially ordered sets, this Journal, vol. 51 (1986), no. 1, pp. 47–58.Google Scholar
[15]Veličković, Boban, Forcing axioms and stationary sets, Advances in Mathematics, vol. 94 (1992), no. 2, pp. 256–284.CrossRefGoogle Scholar
[16]Woodin, W. Hugh, The Axiom of Determinacy, Forcing Axioms, and the Nonstationary Ideal, de Gruyter Series in Logic and its Applications, vol. 1, Walter de Gruyter & Co., Berlin, 1999.CrossRefGoogle Scholar