Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T21:07:04.684Z Has data issue: false hasContentIssue false
  • English
  • Français

HANDMADE DENSITY SETS

Published online by Cambridge University Press:  21 March 2017

GEMMA CAROTENUTO
GEMMA CAROTENUTO*
Affiliation:
DIPARTIMENTO DI MATEMATICA UNIVERSITA’ DI SALERNO SALERNO, ITALYE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a metric space (X , d), equipped with a locally finite Borel measure, a measurable set $A \subseteq X$ is a density set if the points where A has density 1 are exactly the points of A. We study the topological complexity of the density sets of the real line with Lebesgue measure, with the tools—and from the point of view—of descriptive set theory. In this context a density set is always in 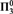$\Pi _3^0$. We single out a family of true 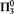$\Pi _3^0$ density sets, an example of true $\Sigma _2^0$ density set and finally one of true 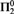$\Pi _2^0$ density set.

Keywords

03E1528A05Lebesgue measuredensity
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 1 , March 2017 , pp. 208 - 223
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andretta, A. and Camerlo, R., The descriptive set theory of the Lebesgue Density Theorem . Advances in Mathematics, vol. 234 (2013), pp. 1–42.CrossRefGoogle Scholar
Andretta, A., Camerlo, R., and Costantini, C., Lebesgue density and exceptional points, http://arxiv.org/abs/1510.04193, 2015.Google Scholar
Carotenuto, G., On the topological complexity of the density sets of the real line, Ph.D. thesis, Università di Salerno, http://elea.unisa.it:8080/jspui/bitstream/10556/1972/1/tesi_G.Carotenuto.pdf, 2015.Google Scholar
Kechris, A. S., Classical descriptive set theory . Advances in Mathematics, vol. 234 (1995), pp. 1–42.Google Scholar
Oxtoby, J. C., Measure and Category: A Survey of the Analogies Between Topological and Measure Spaces, Graduate Texts in Mathematics, Springer-Verlag, New York, 1980.CrossRefGoogle Scholar
Tacchi, J. P., Points of density of Cantor sets . European Journal of Combinatorics, vol. 16 (1995), no. 6, pp. 645–653 (In French).CrossRefGoogle Scholar
Wilczyński, W., Density topologies , Handbook of Measure Theory (Pap, E., editor), North-Holland, Amsterdam, 2002, pp. 675–702.CrossRefGoogle Scholar