Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T14:08:58.057Z Has data issue: false hasContentIssue false
  • English
  • Français

HAMEL SPACES AND DISTAL EXPANSIONS

Published online by Cambridge University Press:  29 August 2019

ALLEN GEHRET  and
TRAVIS NELL
ALLEN GEHRET
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CALIFORNIA LOS ANGELES, LOS ANGELES, CA90095, USA E-mail: [email protected]
TRAVIS NELL
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN URBANA, IL61801, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note, we construct a distal expansion for the structure 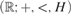$$\left( {; + , < ,H} \right)$$, where 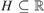$H \subseteq $ is a dense 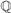$Q$-vector space basis of 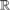$R$ (a so-called Hamel basis). Our construction is also an expansion of the dense pair 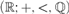$\left( {; + , < ,} \right)$ and has full quantifier elimination in a natural language.

Keywords

Primary 03C64Secondary 03C4506F20distalitydp-rankindependence propertyo-minimalitydense pairsHamel basis
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 1 , March 2020 , pp. 422 - 438
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adler, H., Strong theories, burden, and weight, preprint, 2007.Google Scholar
Aschenbrenner, M., van den Dries, L., and van der Hoeven, J., Asymptotic Differential Algebra and Model Theory of Transseries, Annals of Mathematics Studies, vol. 195, Princeton University Press, Princeton, NJ, 2017.Google Scholar
Chernikov, A. and Simon, P., Externally definable sets and dependent pairs II. Transactions of the American Mathematical Society, vol. 367 (2015), no. 7, pp. 5217–5235.Google Scholar
Chernikov, A. and Starchenko, S., Regularity lemma for distal structures. Journal of the European Mathematical Society, vol. 20 (2018), no. 10, pp. 2437–2466.Google Scholar
Dolich, A. and Goodrick, J., Strong theories of ordered Abelian groups. Fundamenta Mathematicae, vol. 236 (2017), no. 3, pp. 269–296.Google Scholar
Dolich, A., Miller, C., and Steinhorn, C., Expansions of o-minimal structures by dense independent sets. Annals of Pure and Applied Logic, vol. 167 (2016), no. 8, pp. 684–706.Google Scholar
Gehret, A. and Kaplan, E., Distality for the asymptotic couple of the field of logarithmic transseries, arXiv preprint, 2018, arXiv:1802.05732.Google Scholar
Heil, C., A Basis Theory Primer, expanded ed., Applied and Numerical Harmonic Analysis, Birkhäuser/Springer, New York, 2011.Google Scholar
Hieronymi, P. and Nell, T., Distal and non-distal pairs, this Journal, vol. 82 (2017), no. 1, pp. 375–383.Google Scholar
Nell, T., Distal and non-distal behavior in pairs, arXiv preprint, 2018, arXiv:1801.07149.Google Scholar
Simon, P., Distal and non-distal NIP theories. Annals of Pure and Applied Logic, vol. 164 (2013), no. 3, pp. 294–318.Google Scholar
Simon, P., A Guide to NIP Theories, Lecture Notes in Logic, vol. 44, Association for Symbolic Logic, Chicago, IL; Cambridge Scientific Publishers, Cambridge, 2015.Google Scholar
Usvyatsov, A., On generically stable types in dependent theories, this Journal, vol. 74 (2009), no. 1, pp. 216–250.Google Scholar
van den Dries, L., Dense pairs of o-minimal structures. Fundamenta Mathematicae, vol. 157 (1998), no. 1, pp. 61–78.Google Scholar