Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T19:48:59.624Z Has data issue: false hasContentIssue false
  • English
  • Français

GENERIC CODING WITH HELP AND AMALGAMATION FAILURE

Part of: Set theory

Published online by Cambridge University Press:  05 October 2020

SY-DAVID FRIEDMAN  and
DAN HATHAWAY
SY-DAVID FRIEDMAN
Affiliation:
KURT GÖDEL RESEARCH CENTER FOR MATHEMATICAL LOGIC UNIVERSITY OF VIENNAVIENNA, AUSTRIAE-mail: [email protected]
DAN HATHAWAY
Affiliation:
MATHEMATICS DEPARTMENT UNIVERSITY OF VERMONTBURLINGTON, VT05405, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

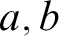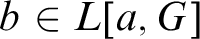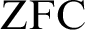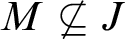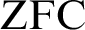We show that if M is a countable transitive model of $\text {ZF}$ and if $a,b$ are reals not in M, then there is a G generic over M such that $b \in L[a,G]$ . 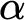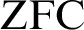We then present several applications such as the following: if J is any countable transitive model of $\text {ZFC}$ and $M \not \subseteq J$ is another countable transitive model of $\text {ZFC}$ of the same ordinal height $\alpha $ , then there is a forcing extension N of J such that $M \cup N$ is not included in any transitive model of $\text {ZFC}$ of height 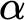$\alpha $ . Also, assuming 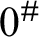$0^{\#}$ exists, letting S be the set of reals generic over L, although S is disjoint from the Turing cone above 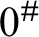$0^{\#}$ , we have that for any non-constructible real a, 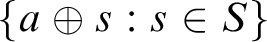$\{ a \oplus s : s \in S \}$ is cofinal in the Turing degrees.

Keywords

forcinginner modelsconstructibilitymodels of set theory

MSC classification

Primary: 03E35: Consistency and independence results 03E40: Other aspects of forcing and Boolean-valued models 03E45: Inner models, including constructibility, ordinal definability, and core models
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 4 , December 2021 , pp. 1385 - 1395
Check for updates
Copyright
© Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baumgartner, J. and Dordal, P., Adjoining dominating functions, this Journal, vol. 50 (1985), no. 1, pp. 94–101.Google Scholar
Brendle, J. and Löwe, B., Eventually different functions and inaccessible cardinals. Journal of the Mathematical Society of Japan, vol. 63 (2011), no. 1, pp. 137–151.10.2969/jmsj/06310137CrossRefGoogle Scholar
Friedman, S., The Hyperuniverse, MALOA lectures at Münster, 2012. Available at http://www.logic.univie.ac.at/~sdf/papers/muenster.2012.pdf Google Scholar
Habi, M., Hamkins, J., Klausner, L., Verner, J., and Williams, K. J., Set-theoretic blockchains. Archive for Mathematical Logic, vol. 58 (2019), no. 7-8, pp. 965-997.10.1007/s00153-019-00672-zCrossRefGoogle Scholar
Hathaway, D., Disjoint Borel functions. Annals of Pure and Applied Logic, vol. 168 (2017), no.8, pp. 1552–1563.10.1016/j.apal.2017.02.004CrossRefGoogle Scholar
Hathaway, D., Disjoint infinity Borel functions, preprint, 2017, http://arxiv.org/abs/1708.09513 Google Scholar
Hathaway, D., Generalized Domination . Doctoral disseratation, The University of Michigan, 2015. Available at http://mysite.du.edu/~dhathaw2/Papers/DanH-ThesisFinal.pdf Google Scholar
Jech, T., Set Theory, the Third Millennium Edition, Revised and Expanded , Springer, New York, 2002.Google Scholar
Palumbo, J., Unbounded and dominating reals in hechler extensions, this Journal, vol. 78 (2013), no. 1, pp. 275–289.Google Scholar
Woodin, H., The Axiom of Determinacy, Forcing Axioms, and the Non-Stationary Ideal, 2nd ed., DE Gruyter, Berlin, Germany/Boston, MA, 2010.10.1515/9783110213171CrossRefGoogle Scholar
Zadrożny, W., Ordinal definability in Jensen’s model, this Journal, vol. 49 (1984), no. 2, pp. 608–620.Google Scholar