Article contents
Generalized quantifiers and elementary extensions of countable models
Published online by Cambridge University Press: 12 March 2014
Extract
Let L be a countable first-order language and L(Q) be obtained by adjoining an additional quantifier Q. Q is a generalization of the quantifier “there exists uncountably many x such that…” which was introduced by Mostowski in [4]. The logic of this latter quantifier was formalized by Keisler in [2]. Krivine and McAloon [3] considered quantifiers satisfying some but not all of Keisler's axioms. They called a formula φ(x) countable-like if
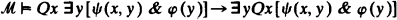
for every ψ. In Keisler's logic, φ(x) being countable-like is the same as ℳ⊨┐Qxφ(x). The main theorem of [3] states that any countable model ℳ of L[Q] has an elementary extension N, which preserves countable-like formulas but no others, such that the only sets definable in both N and M are those defined by formulas countable-like in M. Suppose C(x) in M is linearly ordered and noncountable-like but with countable-like proper segments. Then in N, C will have new elements greater than all “old” elements but no least new element — otherwise it will be definable in both models. The natural question is whether it is possible to use generalized quantifiers to extend models elementarily in such a way that a noncountable-like formula C will have a minimal new element. There are models and formulas for which it is not possible. For example let M be obtained from a minimal transitive model of ZFC by letting Qxφ(x) mean “there are arbitrarily large ordinals satisfying φ”.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1977
References
REFERENCES
- 2
- Cited by


