Article contents
A general treatment of equivalent modalities
Published online by Cambridge University Press: 12 March 2014
Extract
The problem of the nonequivalent modalities available in certain systems is a classical problem of modal logic. In this paper we deal with this problem without referring to particular logics, but considering the whole class of normal propositional logics. Given a logic L let P(L) (the m-partition generated by L) denote the set of the classes of L-equivalent modalities. Obviously, different logics may generate the same m-partition; the first problem arising from this general point of view is therefore to determine the cardinality of the set of all m-partitions. Since, as is well known, there exist 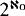 normal logics, and since one immediately realizes that there are infinitely many m-partitions, the problem consists in choosing (assuming the continuum hypothesis) between ℵ0 and
normal logics, and since one immediately realizes that there are infinitely many m-partitions, the problem consists in choosing (assuming the continuum hypothesis) between ℵ0 and 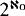 . In Theorem 1.2 we show that there are
. In Theorem 1.2 we show that there are 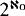 m-partitions, as many as the logics.
m-partitions, as many as the logics.
The next problem which naturally arises consists in determining, given an m-partition P(L), the number of logics generating P(L) (in symbols, μ(P(L))). In Theorem 2.1(ii) we show that ∣{P(L): μ(P(L)) = 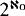 }∣ =
}∣ = 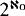 . Now, the set {L′) = P(L)} has a natural minimal element; that is, the logic L* axiomatized by K ∪ {φ(p) ↔ ψ(p): φ, ψ are L-equivalent modalities}; P(L) and L* can be, in some sense, identified, thus making the set of m-partitions a subset of the set of logics.
. Now, the set {L′) = P(L)} has a natural minimal element; that is, the logic L* axiomatized by K ∪ {φ(p) ↔ ψ(p): φ, ψ are L-equivalent modalities}; P(L) and L* can be, in some sense, identified, thus making the set of m-partitions a subset of the set of logics.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1989
References
REFERENCES
- 2
- Cited by


