Article contents
Fusion over sublanguages
Published online by Cambridge University Press: 12 March 2014
Abstract
Generalising Hrushovski's fusion technique we construct the free fusion of two strongly minimal theories T1. T2 intersecting in a totally categorical sub-theory T0. We show that if. e.g., T0 is the theory of infinite vector spaces over a finite field then the fusion theory Tω, exists, is complete and ω-stable of rank ω. We give a detailed geometrical analysis of Tω, proving that if both T1, T2 are 1-based then. Tω can be collapsed into a strongly minimal theory, if some additional technical conditions hold—all trivially satisfied if T0 is the theory of infinite vector spaces over a finite field 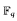 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2006
References
REFERENCES
- 3
- Cited by


