Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T22:03:33.976Z Has data issue: false hasContentIssue false
  • English
  • Français

FORKING AND STABILITY IN THE REPRESENTATIONS OF A C*-ALGEBRA

Published online by Cambridge University Press:  22 July 2015

CAMILO ARGOTY
CAMILO ARGOTY*
Affiliation:
CAMILO ARGOTY ESCUELA DE MATEMÁTICAS UNIVERSIDAD SERGIO ARBOLEDA BOGOTÁ, COLOMBIA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the theory of a nondegenerate representation of a C*-algebra 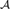${\cal A}$ over a Hilbert space H is superstable. Also, we characterize forking, orthogonality and domination of types.

Keywords

C*-algebrasstabilityHilbert spaces
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 3 , September 2015 , pp. 785 - 796
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akhiezer, N.I. and Glazman, I.M., Theory of operators in Hilbert Space vols. I and II, Pitman Advanced Publishing Program, Boston, 1981.Google Scholar
Arveson, W., A short course on spectral theory, Springer Verlag, New York, 2002.CrossRefGoogle Scholar
Argoty, C., The model theory of modules of a C*-algebra. Archive for Mathematical Logic, vol. 52 (2013), no. 5–6, pp. 525–541.CrossRefGoogle Scholar
Argoty, C. and Berenstein, A., Hilbert spaces expanded with an unitary operator. Mathematical Logic Quarterly, vol. 55 (2009), no. 1, pp. 37–50.CrossRefGoogle Scholar
Argoty, C. and Ben Yaacov, I., Model theory Hilbert spaces expanded with a bounded normal operator, avaliable in http://www.maths.manchester.ac.uk/logic/mathlogaps/preprints/hilbertnormal1.pdf.Google Scholar
Ben Yaacov, I., Modular functionals and perturbations of Nakano spaces. Journal of Logic and Analysis, vol 1 (2009), no. 1, pp. 1–42.Google Scholar
Ben Yaacov, I., Berenstein, A., Henson, C. W. and Usvyatsov, A., Model theory for metric structures, Model Theory with Applications to Algebra and Analysis, volume 2 (Chatzidakis, Zoé, Macpherson, Dugald, Pillay, Anand, and Wilkie, Alex, editors), London Mathematical Society Lecture Note Series, vol. 350 (2008), pp. 315–427.CrossRefGoogle Scholar
Ben Yaacov, I. and Usvyatsov, A., Continuous first order logic and local stability. Transactions of the American Mathematical Society, vol. 362 (2010), pp. 5213–5259.CrossRefGoogle Scholar
Ben Yaacov, I., Usvyatsov, A., and Zadka, M., Generic automorphism of a Hilbert space, preprint.Google Scholar
Berenstein, A. and Buechler, S., Simple stable homogeneous expansions of Hilbert spaces. Annals of pure and Applied Logic, vol. 128 (2004), pp. 75–101.CrossRefGoogle Scholar
Buechler, S., Essential stability theory, Springer Verlag, Berlin, 1991.Google Scholar
Connes, A., Noncommutative geometry, Academis Press, London, 1994.Google Scholar
Davidson, K., C*-algebras by example, Fields institute monographs, American Mathematical Society, Providence, RI, 1996.CrossRefGoogle Scholar
Dixmier, J., Les C*-algebres et leur representations, Bordas, Paris, 1969.Google Scholar
Dunford, N. and Schwarz, J., Linear operators, John Wiley & Sons, New York, 1971.Google Scholar
Farah, I., Hart, B, Sherman, D., Model Theory of Operator Alebras I: Stability. Bulletin of the London Mathematical Society, vol. 45 (2013), pp. 825–838.CrossRefGoogle Scholar
Farah, I., Hart, B, and Sherman, D., Model Theory of Operator Alebras II: Model theory. Israel Journal of Mathematics, vol. 201 (2014), pp. 477–505.CrossRefGoogle Scholar
Henle, M., A Lebesgue decomposition theorem for C*-algebras. Canadian Mathematical Bulletin, vol. 15 (1972), no. 1, pp. 87–91.CrossRefGoogle Scholar
Henson, C. W. and Tellez, H., Algebraic closure in continuous logic. Revista Colombiana de Matemáticas, vol. 41 [Especial] (2007), pp. 279–285.Google Scholar
Iovino, J., Stable theories in functional analysis, Ph.D. Thesis, University of Illinois, Champaign, IL, 1994.Google Scholar
Pedersen, G., C*-algebras and their automorphism groups, Academic Press, London, 1979.Google Scholar
Reed, M. and Simon, B., Methods of modern mathematical physics, Functional analysis, revised and enlarged edition, vol. I, Academic Press, London, 1980.Google Scholar