Article contents
Forcing with Δ perfect trees and minimal Δ-degrees
Published online by Cambridge University Press: 12 March 2014
Extract
This paper is a sequel to [3] and it contains, among other things, proofs of the results announced in the last section of that paper.
In §1, we use the general method of [3] together with reflection arguments to study the properties of forcing with Δ perfect trees, for certain Spector pointclasses Γ, obtaining as a main result the existence of a continuum of minimal Δ-degrees for such Γ's, under determinacy hypotheses. In particular, using PD, we prove the existence of continuum many minimal Δ½n+1-degrees, for all n.
Following an idea of Leo Harrington, we extend these results in §2 to show the existence of minimal strict upper bounds for sequences of Δ-degrees which are not too far apart. As a corollary, it is computed that the length of the natural hierarchy of Δ½n+1-degrees is equal to ω when n ≥ 1. (By results of Sacks and Richter the length of the natural hierarchy of 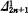 -degrees is known to be equal to the first recursively inaccessible ordinal.)
-degrees is known to be equal to the first recursively inaccessible ordinal.)
We will follow in this paper standard notation and terminology, as in Moschovakis' book [7]. Letters e, i, j, k, l, m, n vary over the set of natural numbers ω, a, b, c over the Cantor space 2ω and α, β, γ, δ, … over the set of reals ωω. Finally ξ, η, κ, λ always denote ordinals.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1981
References
REFERENCES
- 1
- Cited by


