Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T10:05:44.439Z Has data issue: false hasContentIssue false
  • English
  • Français

THE FLUTED FRAGMENT REVISITED

Published online by Cambridge University Press:  06 June 2019

IAN PRATT-HARTMANN ,
WIESŁAW SZWAST  and
LIDIA TENDERA
IAN PRATT-HARTMANN
Affiliation:
SCHOOL OF COMPUTER SCIENCE MANCHESTER UNIVERSITY MANCHESTER, M13 9PL, UK and INSTYTUT INFORMATYKI UNIWERSYTET OPOLSKI 45-040 OPOLE, POLAND E-mail: [email protected]
WIESŁAW SZWAST
Affiliation:
INSTYTUT INFORMATYKI UNIWERSYTET OPOLSKI 45-040 OPOLE, POLANDE-mail: [email protected]
LIDIA TENDERA
Affiliation:
INSTYTUT INFORMATYKI UNIWERSYTET OPOLSKI 45-040 OPOLE, POLANDE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the fluted fragment, a decidable fragment of first-order logic with an unbounded number of variables, motivated by the work of W. V. Quine. We show that the satisfiability problem for this fragment has nonelementary complexity, thus refuting an earlier published claim by W. C. Purdy that it is in NExpTime. More precisely, we consider 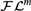${\cal F}{{\cal L}^m}$, the intersection of the fluted fragment and the m-variable fragment of first-order logic, for all 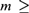$m \ge 1$. We show that, for 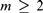$m \ge 2$, this subfragment forces 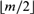$\left\lfloor {m/2} \right\rfloor$-tuply exponentially large models, and that its satisfiability problem is 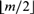$\left\lfloor {m/2} \right\rfloor$-NExpTime-hard. We further establish that, for 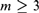$m \ge 3$, any satisfiable 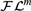${\cal F}{{\cal L}^m}$-formula has a model of at most (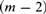$m - 2$)-tuply exponential size, whence the satisfiability (= finite satisfiability) problem for this fragment is in (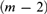$m - 2$)-NExpTime. Together with other, known, complexity results, this provides tight complexity bounds for 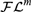${\cal F}{{\cal L}^m}$ for all 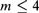$m \le 4$.

Keywords

68Q17first-order logicdecidabilitysatisfiabilitytransitivitycomplexity
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 3 , September 2019 , pp. 1020 - 1048
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andréka, H., van Benthem, J., and Németi, I., Modal languages and bounded fragments of predicate logic. Journal of Philosophical Logic, vol. 27 (1998), no. 3, pp. 217–274.Google Scholar
Börger, E., Grädel, E., and Gurevich, Y., The Classical Decision Problem, Springer, Berlin, 1997.Google Scholar
Grädel, E., On the restraining power of guards, this Journal, vol. 64 (1999), no. 4, pp. 1719–1742.Google Scholar
Grädel, E., Kolaitis, P., and Vardi, M., On the decision problem for two-variable first-order logic. Bulletin of Symbolic Logic, vol. 3 (1997), no. 1, pp. 53–69.Google Scholar
Herzig, A., A new decidable fragment of first-order logic, Abstracts of the 3rd Logical Biennial Summer School and Conference in Honour of S. C. Kleene, Varna, Bulgaria, 1990June .Google Scholar
Hustadt, U., Schmidt, R., and Georgieva, L., A survey of decidable first-order fragments and description logics. Journal of Relational Methods in Computer Science, vol. 1 (2004), no. 3, pp. 251–276.Google Scholar
Lutz, C. and Sattler, U., The complexity of reasoning with Boolean modal logics, Advances in Modal Logic, vol. 3 (Wolter, F., Wansing, H., de Rijke, M., and Zakharyaschev, M., editors), CLSI Publications, Menlo Park, 2002, pp. 329–348.Google Scholar
Mortimer, M., On languages with two variables. Mathematical Logic Quarterly, vol. 21 (1975), no. 1, pp. 135–140.Google Scholar
Noah, A., Predicate-functors and the limits of decidability in logic. Notre Dame Journal of Formal Logic, vol. 21 (1980), no. 4, pp. 701–707.Google Scholar
Plaisted, D. and Greenbaum, S., A structure-preserving clause form translation. Journal of Symbolic Computation, vol. 2 (1986), no. 3, pp. 293–304.Google Scholar
Pratt-Hartmann, I., Szwast, W., and Tendera, L., Quine’s fluted fragment is nonelementary, 25th EACSL Annual Conference on Computer Science Logic, CSL 2016 (Talbot, J.-M. and Regnier, L., editors), Leibniz International Proceedings in Informatics, vol. 62, Schloß Dagstuhl—Leibniz-Zentrum für Informatik, Dagstuhl, 2016, pp. 39:1–39:21.Google Scholar
Purdy, W., Decidability of fluted logic with indentity. Notre Dame Journal of Formal Logic, vol. 37 (1996), no. 1, pp. 84–104.Google Scholar
Purdy, W., Fluted formulas and the limits of decidability, this Journal, vol. 61 (1996), no. 2, pp. 608–620.Google Scholar
Purdy, W., Quine’s limits of decision, this Journal, vol. 64 (1999), no. 4, pp. 1439–1466.Google Scholar
Purdy, W., Complexity and nicety of fluted logic. Studia Logica, vol. 71 (2002), pp. 177–198.Google Scholar
Quine, W. V., On the limits of decision, Proceedings of the 14th International Congress of Philosophy, vol. III, Herder, Vienna, 1969, pp. 57–62.Google Scholar
Quine, W. V., Algebraic logic and predicate functors, The Ways of Paradox, revised and enlarged ed., Harvard University Press, Cambridge, MA, 1976, pp. 283–307.Google Scholar
Quine, W. V., The variable, The Ways of Paradox, revised and enlarged ed., Harvard University Press, Cambridge, MA, 1976, pp. 272–282.Google Scholar
Schmidt, R. and Hustadt, U., A resolution decision procedure for fluted logic, Automated Deduction—CADE-17 (McAllester, D., editor), Lecture Notes in Artificial Intelligence, vol. 1831, Springer-Verlag, Berlin, 2000, pp. 433–448.Google Scholar
Schmitz, S., Complexity hierarchies beyond Elementary. ACM Transactions on Computation Theory, vol. 8 (2016), no. 1, pp. 3:1–3:26.Google Scholar
Stockmeyer, L., The complexity of decision problems in automata and logic , Ph.D. thesis, Massachusetts Institute of Technology, Computer Science Laboratory, 1974, Report MAC-TR-133.Google Scholar
Vardi, M., On the complexity of bounded-variable queries, Proceedings of the Fourteenth ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems, ACM Digital Library, 1995, pp. 266–276.Google Scholar
Voigt, M., A fine-grained hierarchy of hard problems in the separated fragment, 32nd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS, 2017, IEEE Xplore Digital Library, 2017, pp. 1–12.Google Scholar